
- •Введение
- •Глава 1. Элементы векторного анализа
- •1. Векторы и действия над ними
- •2. Математическое понятие поля. Градиент
- •3. Дивергенция. Теорема Остроградского-Гаусса
- •4. Ротор. Теорема Стокса
- •5. Некоторые соотношения векторного анализа
- •6. Операции в криволинейных координатах
- •В цилиндрических координатах
- •В сферических координатах
- •7. О дифференциальных уравнениях с частными производными
- •Глава 2. Уравнения лапласа и пуассона
- •8. Дельта-функция Дирака
- •9. Интегрирование уравнения Пуассона
- •10. Граничные задачи для уравнения Лапласа
- •11. Метод разделения переменных
- •Глава 3. Гармонические колебания и волны
- •12. Гармонические колебания и метод комплексных амплитуд
- •13. Волновые процессы и их математическое описание
- •14. Вращение декартовой системы координат
- •Глава 4. Решения волновых уравнений
- •15. Интегрирование неоднородного уравнения Гельмгольца и уравнения Даламбера
- •16. Уравнение Бесселя и цилиндрические функции
- •17. Решение однородного уравнения Гельмгольца методом разделения переменных
- •Глава 5. Краевые задачи электродинамики
- •18. Граничные задачи для уравнения Гельмгольца.Собственные функции и собственные значения
- •19. Ортогональные системы функций и ряды Фурье
- •20. Сведения из алгебры
- •21. Проекционные методы
- •Список литературы
- •Контрольные задания
13. Волновые процессы и их математическое описание
13.1. Плоская однородная
волна. Пусть
имеется какой-то физический
процесс, распространяющийся в прямолинейном
направлении z
с постоянной
скоростью v.
В простейшем
случае это означает, что, если
где-либо было отмечено состояние
процесса, характеризуемое величинойи
=а, то через промежуток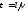 это состояние окажется смещенным
вдоль осиz на
величину отрезкаl.
Положим, что в начале координат (z
= 0) состояние изменяется по законуu
= u(t),
тогда в произвольной точкеz
> 0 в результате запаздывания на
время распространенияz/v:
это состояние окажется смещенным
вдоль осиz на
величину отрезкаl.
Положим, что в начале координат (z
= 0) состояние изменяется по законуu
= u(t),
тогда в произвольной точкеz
> 0 в результате запаздывания на
время распространенияz/v:
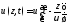 (13.1)
(13.1)
Будем считать, что выражение (13.1) определяет функцию во всём пространстве (по осям х и y никаких изменений не происходит), и назовем рассматриваемый процесс плоской однородной волной. Дело в том, что, положив z = const, мы задаём плоскость, в которой мгновенное значение фазы функции и постоянно; она называется фронтом волны. Взяв в некоторый моментt фронт, для которогои = а, легко убедиться, что с течением времени он движется вдоль осиz со скоростьюv.
Ясно, что выражение
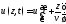 (13.1а)
(13.1а)
тоже определяет плоскую однородную волну, отличающуюся от рассмотренной тем, что она распространяется в противоположном направлении минусz. Действительно, (13.1а) получается из (13, 1) при заменеv на -v.
Обратимся к волновому уравнению (§ 7 п. 2)
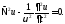 (13
2)
(13
2)
Используя декартовы координаты и рассматривая лишь функции, отражающие отсутствие изменений по осям х и y (ди/дх = ди/ду = 0), приводим его к виду:
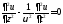 (13.3)
(13.3)
Взяв
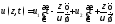 (13.4)
(13.4)
где u1 и и2 - произвольные дважды дифференцируемые функции, путем непосредственной подстановки в (13.3) убеждаемся, что это - решение. Можно доказать, что формула (13.4) выражает общее решение одномерного волнового уравнения(13.3). На основании предыдущего мы можем утверждать, что оно описывает суперпозицию двух произвольных плоских однородных волн, распространяющихся навстречу друг другу со скоростью υ. В частности, при u2 = 0 и, соответственно, при u1= 0 возникают решения вида (13.1) и (13.1а).
13.2. Гармоническая
волна. Взяв в (13.1) такую функциюи(z,t),
что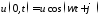 ,
приходим к весьма важному
частному виду плоской однородной волны:
,
приходим к весьма важному
частному виду плоской однородной волны:
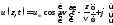 ,
,
или
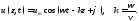 (13.5)
(13.5)
Это плоская однородная гармоническая волна; введённый параметрk называетсяволновым числом.
Как видно из (13.5), полная фаза гармонических колебаний ωt - kz + φ, при заданном t убывает пропорционально z; значения функции u(z, t) при этом периодически повторяются. Пространственный период называют длиной волны λ. Очевидно, для произвольногоz должно быть:
u (z +λ,t) - и (z, t).
Поэтому из (13.5) следует, что kλ = 2π, т. е.
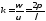 , (13.6)
, (13.6)
а также
v=λf, (13.7)
где f = ω/2π - частота процесса (§ 12 п. 1). Заметим, что вданном случае v называется фазовой скоростью.
Чтобы составить более наглядное представление о гармонической волне, положим сначала в (13.5)t = 0 и получим
и (z, 0) = ит cos (-kz + φ) = ит cos (kz - φ),
т. е. функцию, характеризующую распределение величины и вдоль оси z в начальный момент t = 0. Эта косинусоида представляет собой как бы «мгновенныйснимок» процесса. Выберем следующий фиксированный моментt> 0 и для него запишем:
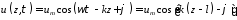 ,
,
где
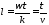
есть не что иное, как расстояние, пройденное волной за истекшее время τ. «Мгновенный снимок», соответствующий моменту τ, дает, таким образом, косинусоиду, сдвинутую по оси z на расстояниеl. Итак, распространение рассматриваемой гармонической волны - это движение косинусоидального распределенияи вдоль прямой с постоянной скоростью.
Плоскую однородную гармоническую волну мы должны получить как частное решение волнового уравнения (13.3). Поскольку речь идет о гармонических колебаниях с частотой ω (п.12.1), применим метод комплексных амплитуд (п.12.2), в результате чего (13.3) перейдет в одномерное уравнение Гельмгольца, т. е. обыкновенное дифференциальное уравнение
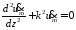 (13.8)
(13.8)
Его решение возьмем в форме второй строчки (7.8):
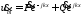 (13.9)
(13.9)
Точки над Р иQ
поставлены, чтобы подчеркнуть, что
это, вообще говоря, произвольные
комплексные константы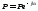 и
и .
Чтобы найтии, возьмём в соответствии
с (12.5)
.
Чтобы найтии, возьмём в соответствии
с (12.5) ;
это дает:
;
это дает:
и (z, t) = P cos(ω t –kz + φ) +Q cos(ωt +kz +φ). (13.10)
Найденное решение уравнения (13.3) выражает суперпозицию двух гармонических волн, распространяющихся со скоростью υ в противоположных направлениях. Гармоническая волна, движущаяся вдоль осиz, возникает как частное решение приQ= 0.
В качестве другого частного решения рассмотрим суперпозицию бегущих навстречу волн с одинаковыми амплитудами Р =Qи начальными фазами φ = ψ. При этом из (13.10) получаем:
и (z, t) = 2Рcoskzcos(ωt+ φ) (13.11).
Описываемый процесс называется стоячей волной. Его отличительной особенностью является синфазность колебаний во всём пространстве. Действительно, фаза ωt + φ зависит только от времени и постоянна для всехz; в зависимости отz, косинусоидально изменяется амплитуда гармонических колебанийит = 2P cos kz. Косинусоидальное распределение вдоль осиz не движется (в отличие от бегущей волны), а испытывает синфазные гармонические колебания; при этом расстояния между соседними нулями («узлами») и максимумами («пучностями») распределения равныλ/2.
13.3. Волны затухающие, неоднородные и неплоские. Гармоническая волна (13.6) называется однородной потому, что её амплитудаит не зависит от поперечных (по отношению к направлению распространения) координатх иу, и плоской - так как для любого момента времениt = constповерхность постоянной фазыωt – kz + φ=const(фронт гармонической волны) является плоскостью.
Плоской однородной будет, следовательно, также гармоническая волна
и(z, t) = ит(z) cos(ωt -kz), (13.12)
амплитуда которой зависит от продольной координаты z, и, в частности, затухающая волна
u(z, t) =um e-k΄΄z cos(ωt -k'z), (k">0) (13.13)
с амплитудой, уменьшающейся экспоненциально по мере ее распространения; параметр k" называется коэффициентом затухания. Формально к выражению (13.13) нетрудно придти, разыскивая решение уравнения (13.8) при комплексномk = k' - jk".
Плоской неоднородной является гармоническая волна
и(х, у, z, t) =ит(х, у) cos(ωt - kz) (13.14)
с амплитудой, зависящей от поперечных координат; её амплитуда может быть и функцией продольной координаты, так что в (13.14) вместо ит (х, у) будетит (х, у, z).
Гармоническая волна, описываемая
выражением
и(х, у, z, t)= ит(х, у, z) cos[ω t - φ(х, у, z)], (13.15)
- неоднородная и неплоская. Её фронт, т. е. поверхность постоянной фазы в заданный момент времени, определяется уравнением
φ(x, у, z) =const. (13.16)
Например, может быть φ(х, у, z) =kr+φ0 (φ0 =const), гдеr-сферическая радиальная координата; при этом (13.16) есть уравнение сферической поверхностиkr=const. Волну такого рода называют сферической. Если жеr - цилиндрическая радиальная координата, то фронт волны - цилиндрическая поверхность, и её называют цилиндрической волной.
Рассмотрим пример однородной сферической волны. Это гармоническая волна, для которой на поверхности сферического фронта амплитуда постоянна:
u(r, t) = ит(r) cos(ωt - kr + φ0). (13.17)
Нетрудно убедиться, что волна такого типа выражается частным решением уравнения (13.2) в сферических координатах, которое при отсутствии зависимости от угловых координат и согласно (6.21) принимает вид:
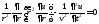 . (13.18)
. (13.18)
Общее решение этого уравнения при гармонических колебаниях с частотой ωесть
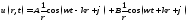 (13.19)
(13.19)
(рекомендуется проделать подстановку (13.19) в (13.18) и убедиться, что уравнение удовлетворяется). Частное решение и (r, t) приВ = 0 даёт волну типа (13.17).
Такая волна возникает при действии «точечного» источника в однородной изотропной среде и называется расходящейся: при распространении волны её сферический фронт расширяется. Любой участок фронта на достаточно больших расстояниях от источника близок к плоскому, так что локально сферическая волна может рассматриваться как плоская.
Частное решение, получаемое из (13.19) при А = 0, выражает сходящуюся сферическую волну: каждый её фронт, приходя из бесконечности, сужается в точку. В большинстве случаев это решение не имеет физического содержания.
Электромагнитные волны, которые будут предметом нашего внимания в курсе электродинамики, отличаются от всех рассмотренных выше тем, что они описываются векторными функциями, т. е. как говорят, являются векторными волнами. Однако им свойственны некоторые особенности, показанные здесь на примерах скалярных волн.
