
- •Введение
- •Глава 1. Элементы векторного анализа
- •1. Векторы и действия над ними
- •2. Математическое понятие поля. Градиент
- •3. Дивергенция. Теорема Остроградского-Гаусса
- •4. Ротор. Теорема Стокса
- •5. Некоторые соотношения векторного анализа
- •6. Операции в криволинейных координатах
- •В цилиндрических координатах
- •В сферических координатах
- •7. О дифференциальных уравнениях с частными производными
- •Глава 2. Уравнения лапласа и пуассона
- •8. Дельта-функция Дирака
- •9. Интегрирование уравнения Пуассона
- •10. Граничные задачи для уравнения Лапласа
- •11. Метод разделения переменных
- •Глава 3. Гармонические колебания и волны
- •12. Гармонические колебания и метод комплексных амплитуд
- •13. Волновые процессы и их математическое описание
- •14. Вращение декартовой системы координат
- •Глава 4. Решения волновых уравнений
- •15. Интегрирование неоднородного уравнения Гельмгольца и уравнения Даламбера
- •16. Уравнение Бесселя и цилиндрические функции
- •17. Решение однородного уравнения Гельмгольца методом разделения переменных
- •Глава 5. Краевые задачи электродинамики
- •18. Граничные задачи для уравнения Гельмгольца.Собственные функции и собственные значения
- •19. Ортогональные системы функций и ряды Фурье
- •20. Сведения из алгебры
- •21. Проекционные методы
- •Список литературы
- •Контрольные задания
21. Проекционные методы
21.1. Исходные представления. Метод Галёркина. Вернемся к рядам Фурье (п.19.3), чтобы провести следующее сравнение.
Пусть в трехмерном пространстве выбрана
декартова система координат и,
следовательно, имеются три единичных
взаимно перпендикулярных вектора:
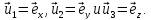
Взяв произвольный вектор
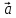 ,
мы можем разложить его по этим ортам
(рис.21.1),что
даёт:
,
мы можем разложить его по этим ортам
(рис.21.1),что
даёт:
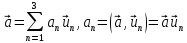 (21.1)
(21.1)
Вектор
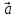 теперь представлен при
помощи трёх своих проекций
теперь представлен при
помощи трёх своих проекций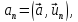 являющихся скалярными произведениями
являющихся скалярными произведениями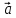 на единичныебазисные векторы
на единичныебазисные векторы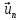 .
.
Сопоставляя (21.1) и (19.13),замечаем отчётливую формальную аналогию
между построенным разложением обычного
вектора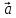 и рядом Фурье функции
и рядом Фурье функции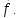 Функция подобна вектору в бесконечномерном
пространстве, а её ряд Фурье можно
рассматривать как разложение этого
вектора в базисе, образованном
ортонормированной системой
Функция подобна вектору в бесконечномерном
пространстве, а её ряд Фурье можно
рассматривать как разложение этого
вектора в базисе, образованном
ортонормированной системой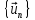 .
.
Далее, пусть поставлена задача (быть может, некоторая граничная задача электродинамики) в виде
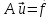 , (21.2)
, (21.2)
где A
- дифференциальный
оператор, заданный с надлежащими
граничными условиями. Разность
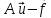 равна нулю,
а потому равны
нулю её проекции на базис
равна нулю,
а потому равны
нулю её проекции на базис
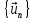 ,
коэффициенты Фурье
,
коэффициенты Фурье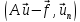 :
:
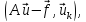 k = 1, 2, …, ∞ (21.3)
k = 1, 2, …, ∞ (21.3)
В большинстве случаев замкнутые аналитические решения задач типа (21.2) недоступны. Но существуют методы, позволяющие получать приближенные решения, которые могут быть как угодно близки к рядам Фурье настоящих решений. Такие методы называются проекционными.
Проекционный метод
Галёркина состоит в том, что строится
представление решения
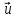 в виде суммы
в виде суммы
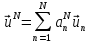 (21.4)
(21.4)
с неопределёнными
коэффициентами
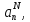 и вместо
(21.3) берутся N
аналогичных
соотношений ортогональности
и вместо
(21.3) берутся N
аналогичных
соотношений ортогональности
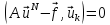 ;k = 1, 2, …,N. (21.5)
;k = 1, 2, …,N. (21.5)
(разумеется, должно быть
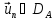 ,
п.19.1). Легко видеть,что
эти соотношения порождают систему
линейных уравнений
,
п.19.1). Легко видеть,что
эти соотношения порождают систему
линейных уравнений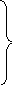
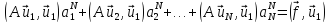
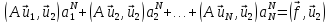

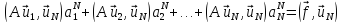
относительно коэффициентов ап как неизвестных, т. е. в матричной форме:
MaN=f, (21.6а)
где в левой части фигурирует вектор,
образованный этими коэффициентами
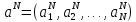 и матрицаМ с элементами
и матрицаМ с элементами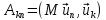 ,а в правой части - заданный вектор
,а в правой части - заданный вектор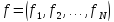 с компонентами
с компонентами
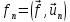 (ср. п. 20.1:
векторы aN
иf - это то же,
чтох иb в п.
20.1). Таким образом, метод
Галёркина сводит граничную задачу
(21.2) к системе линейных
уравнений (21.6), решение которой определяет
коэффициенты представления (21.4).
(ср. п. 20.1:
векторы aN
иf - это то же,
чтох иb в п.
20.1). Таким образом, метод
Галёркина сводит граничную задачу
(21.2) к системе линейных
уравнений (21.6), решение которой определяет
коэффициенты представления (21.4).
Возьмём теперь задачу на собственные значения вида
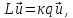 (21.7)
(21.7)
где L - некоторый дифференциальный оператор, а q - функция координат. Подобно (21.3) имеем:
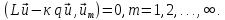 (21.8)
(21.8)
Построив представление решения вида (21.4), подчиним его N условиям ортогональности:
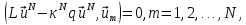 (21.9)
(21.9)
подобно тому, как это делалось выше; индекс N при κ подчёркивает, что имеются в виду приближённые собственные значения. Из (21.9) следует однородная система линейных уравнений
MaN = κNQaN, (21.10)
где матрицы М
и Q
имеют элементы
Mkn
= (Lun,
uk)
и
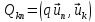 соответственно.
соответственно.
Таким образом, первые N собственных
значений задачи (21.7) приближённо
определяются как корни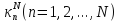 характеристического уравнения
характеристического уравнения
Det|M - κNQ| = 0 (21.11)
(п. 20.3). Если, в частности q=1, то (21.11) имеет вид
Det|M - κNI| = 0, (21.11a)
что совпадает с (20.20). Приближёнными собственными значениями задачи (21.7) являются при этом собственные значения матрицыМ.
Для широкого класса задач доказывается сходимость метода Галёркина, т. е. устанавливается тот факт, что
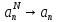 при
при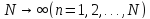 , (21.12)
, (21.12)
где ап
- коэффициенты
Фурье решения
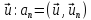 .
.
21.2. Вариационные принципы и метод Ритца. Рассматривая задачу на собственные значения (21.7), будем считать, что оператор L симметрический, функция q вещественна, а собственные значения κn образуют последовательность вида (19.9).
Пусть
 - произвольная функция
- произвольная функция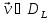 .
Запишем выражение
.
Запишем выражение
 (21.13)
(21.13)
Легко видеть, что если
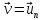 - одна из собственных функций, то
- одна из собственных функций, то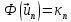 есть
соответствующее собственное значение.
есть
соответствующее собственное значение.
Выражение (21.13), в котором
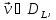 может изменяться
в некотором классе функций, относится
к так называемым функционалам
(функционал
- «функция от функции»). Можно
показать, что функционал
может изменяться
в некотором классе функций, относится
к так называемым функционалам
(функционал
- «функция от функции»). Можно
показать, что функционал
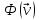 имеет минимум, который равен низшему
собственному значениюv1:
имеет минимум, который равен низшему
собственному значениюv1:
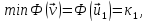 (21.14)
(21.14)
а каждое высшее собственное значение есть также минимум Ф(u), но при некотором дополнительном условии, а именно
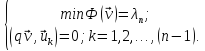 (21.15)
(21.15)
Говорят, что
функционал
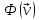 (21.13) выражает
вариационный
принцип для
задачи (21.7);
вычисление собственных значений
(21.13) выражает
вариационный
принцип для
задачи (21.7);
вычисление собственных значений
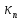 можно свести квариационной
задаче нахождения
можно свести квариационной
задаче нахождения
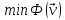 (21.15) при переборе всевозможных
(21.15) при переборе всевозможных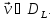 Какчастную
форму функционала (21.13) следует
рассматривать выражение
(19.6), (19.7) и (19.8). Существуют также
вариационные принципы совершенно иного
рода, не имеющие связи с задачами на
собственные значения. К ним, например,
относится принцип Ферма [1].
Какчастную
форму функционала (21.13) следует
рассматривать выражение
(19.6), (19.7) и (19.8). Существуют также
вариационные принципы совершенно иного
рода, не имеющие связи с задачами на
собственные значения. К ним, например,
относится принцип Ферма [1].
Ограничивая класс
функций, будем искать вместо
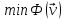 величину
величину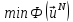 ,
где
,
где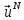 есть представление (21.4) решения
задачи (21.7); при этом варьируются
коэффициенты
есть представление (21.4) решения
задачи (21.7); при этом варьируются
коэффициенты
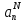 .
Внося (21.4) в (21.13), имеем:
.
Внося (21.4) в (21.13), имеем:
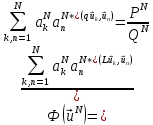 (21.15)
(21.15)
Это функция переменных
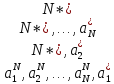 (комплексно сопряженные коэффициенты
- независимые переменные),
и чтобы определить минимум данной
функции, надо составить и обратить в
нуль производные по всем переменным:
условие необходимое, хотя и, вообще
говоря, недостаточное. Величину
(комплексно сопряженные коэффициенты
- независимые переменные),
и чтобы определить минимум данной
функции, надо составить и обратить в
нуль производные по всем переменным:
условие необходимое, хотя и, вообще
говоря, недостаточное. Величину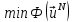 примем за выражение приближённых
собственных значенийκN.
Составляя равенства
примем за выражение приближённых
собственных значенийκN.
Составляя равенства
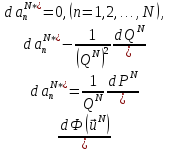
получаем:
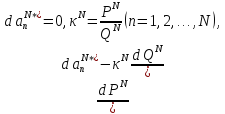 (21.17)
(21.17)
т.е
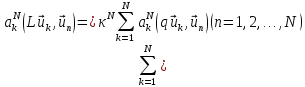
или в матричной форме с использованием обозначений из п. 1:
MaN = κNQaN, (21.18)
что совпадает с результатом (21.10), полученным методом Галёркина. Способ, которым было найдено матричное уравнение (21.18), также относится к проекционным методам и называетсяметодом Ритца.
Для задачи (21.2), если оператор А симметрический, тоже можно сформулировать вариационный принцип в виде функционала
 (21.19)
(21.19)
Применяя метод Ритца, в данном случае придём к матричному уравнению(21.6а).
Уравнения (21.10), (21.6 а) и аналогичные алгебраические формы, к которым сводится граничная задача путём применения проекционных методов, называются уравнениями Галёркина-Ритца.
