
- •Ленинградский институт авиационного приборостроения
- •Отражение
- •Явление вторичного излучения радиоволн
- •Виды отражения
- •Зеркальное отражение
- •Диффузное отражение
- •2.2.1. Критерий зеркальности - диффузности
- •Резонансное отражение.
- •Диапазон волн, используемых в радиолокации
- •4. Металлический зеркальный шар как радиолокационная цель.Метод геометрической оптики
- •5. Уравнение дальности
- •6. Эффективная площадь рассеяния цели
- •7. Метод волновой оптики. Эпр шара при произвольном соотношении r и
- •8. Блестящая точка. Эпр тел двоякой кривизны
- •9. Плоский отражатель
- •10. Уголковый отражатель
- •11. Полуволновый вибратор и ответчик ван-атта
- •12. Эпр двух отражателей, находящихся
- •13. Фазовый фронт вторичной волны двух отражателей
- •14. Эпр множества отражателей, находящихся в пределах разрешаемого объёма
- •15. Эпр реальных целей
- •16. Характер флюктуаций амплитуды отражённых импульсов
- •17. Разрешаемый объём. Точечные цели. Пространственно- и объёмно-распределённые цели
- •18. Влияние на эпр поляризации излучаемыхи принимаемых радиоволн
- •19. Противорадиолокационные покрытия
- •20. Методы измерения эпр
- •Указатель литературы
- •Оглавление
14. Эпр множества отражателей, находящихся в пределах разрешаемого объёма
Рассмотрим теперь случай, когда напряжение на входе приёмника определяется суммой сигналов, отражённых от n отдельных элементов,
 (56)
(56)
Здесь Um i и i — амплитуда и фаза сигнала, отражённого i-м элементом цели.
Преобразуем выражение (56)

где
 (57)
(57)
![]() (58)
(58)
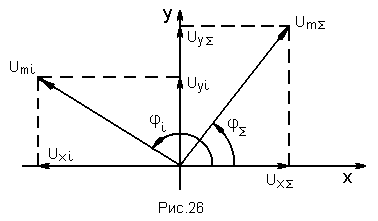
Смысл произведённых преобразований заключается в том, что мы каждое i-e входное напряжение разложили на две квадратурные составляющие (или на две проекции Uxi, Uyi по осям x и у, рис. 26), затем нашли амплитуды результирующих квадратурных составляющих UxΣ, UyΣ путём алгебраического суммирования n слагаемых и, наконец, в результате геометрического суммирования UxΣ и UyΣ нашли амплитуду UmΣ и фазу Σ напряжения на входе приёмника. Итак, будем иметь
uвх(t) = UmΣ cos(t -Σ) . (59)
Если расположение элементов в пространстве хаотически изменяется, то и фазы i изменяются случайным образом. При этом амплитуды квадратурных составляющих Uxi = Umi cos i и Uyi = Umi sin i - также будут случайными.
Предположим, что амплитуды отдельных составляющих входного сигнала Umi примерно одинаковы, что имеет место при соизмеримых значениях ЭПР отдельных элементов. Тогда законы распределения квадратурных составляющих Uxi и Uyi будут мало отличаться. В этих условиях законы распределения случайных величин UxΣ и UyΣ, являющихся результатом суммирования n случайных слагаемых, согласно центральной предельной теореме теории вероятностей будут нормализоваться по мере увеличения n. В частном случае, когда амплитуды всех составляющих входного напряжения одинаковы (одинаковы ЭПР всех элементов), законы распределения UxΣ и UyΣ близки к нормальному уже при n 4 5. Итак, будем считать, что UxΣ и UyΣ распределены нормально

где W — плотность вероятности; 2x = 2y = 2 - дисперсии напряжений UxΣ и UyΣ.
Найдём закон распределения амплитуды входного сигнала UmΣ. Вначале покажем, что случайные величины Uxi = Umi cos i и Uyi = Umi sin i некоррелированы. Будем считать, что фаза i равномерно распределена на интервале [0, 2], т.е.

Тогда ковариация этих величин
![]()
Случайные величины UxΣ и UyΣ будут также некоррелированными, поскольку каждое из слагаемых UxΣ взаимно некоррелировано с каждым из слагаемых UyΣ. Для нормально распределённых случайных величин некоррелированность означает и независимость, поэтому двумерная плотность вероятности совместного распределения UxΣ и UyΣ равна произведению одномерных плотностей
 (60)
(60)
От двумерного распределения (60) перейдём к двумерному закону распределения случайных величин UmΣ и Σ, использовав соотношения (58).
Если случайные величины UxΣ и UyΣ принимают значения в некоторых пределах [UxΣ, UxΣ + dUxΣ], [UyΣ, UyΣ + dUyΣ], то функционально зависящие от них величины UmΣ и Σ могут принять значения только в пределах [UmΣ, UmΣ + dUmΣ] и [Σ, Σ + dΣ], которые определяются выражениями (58). Вероятность, что эти величины будут находиться в указанных пределах, равна
W (UxΣ , UyΣ ) dUxΣ dUyΣ = W (UmΣ, Σ ) dUmΣ dΣ . (61)
Обозначим dS1 = dUxΣ dUyΣ; dS2 = dUmΣ dΣ - элементарные площади в координатах UxΣ , UyΣ и UmΣ, Σ. Из соотношения (61) получим
W (UmΣ, Σ ) = W (UxΣ , UyΣ ) d S1 / dS2 . (62)
Отношение элементарных площадей при переходе от одной системы координат к другой определяется якобианом преобразования
 (63)
(63)
Подставляя в формулу (62) необходимые выражения из формул (61) и (63) и используя соотношение из формул (58) U2mΣ = U2xΣ + U2yΣ, получим окончательное выражение для совместной плотности распределения UmΣ и Σ
 (64)
(64)
От двумерного распределения (64) перейдем к одномерному, произведя усреднение по Σ в пределах возможных значений фазы [0, 2],
 (65)
(65)
Соотношение (65) определяет известный в теории вероятностей закон распределения Релея. Следовательно, результирующая амплитуда суммы сигналов, отражённых от находящихся в пределах разрешаемого объёма хаотически перемещающихся n элементов с примерно одинаковыми ЭПР, подчинена закону распределения Релея, если n достаточно велико. Кривая плотности распределения Релея при нормированном к параметру σ аргументе представлена на рис. 27.
Найдём закон распределения мощности входного сигнала
![]() (66)
(66)
где Rвх - входное сопротивление приёмника.

При переходе от переменной UmΣ к переменной PΣ для вероятности пребывания этих величин в пределах [UmΣ, UmΣ + dUmΣ]; [PΣ, PΣ + dPΣ] можно написать выражение
W(PΣ) dPΣ =W(UmΣ) dUmΣ,
откуда
![]() (67)
(67)
Из формулы (66) получим
 (68)
(68)
Подставляя в (67) соответствующие выражения из формул (65), (66) и (68), получим
 (69)
(69)
Заметим, что среднее значение мощности отражённого сигнала
 (70)
(70)
Из формул (69) и (70) окончательно получим
 (71)
(71)
Учитывая, что ЭПР пропорциональна мощности отражённого сигнала
![]()
для плотности вероятности ЭПР получим выражение
 (72)
(72)
Таким образом, суммарная мощность сигналов, отражённых от множества хаотически перемещающихся элементов, и результирующая ЭПР всей цели изменяются случайным образом в соответствии с экспоненциальными законами распределения (71) и (72) (рис. 28).
Вероятность того, что величина ЭПР не превысит заданное значение SЭ, определяется интегральным законом распределения
 (73)
(73)

Если ЭПР непрерывно случайным образом изменяется во времени, то соотношение (73) определяет вероятность того, что мгновенное значение ЭПР в произвольно выбранный момент времени будет меньше заданного значения. Интегральный закон распределений нормированного значения ЭПР представлен на рис. 29.
Если наблюдение цели производится в течение интервала времени, достаточно большого по сравнению с временем корреляции случайного процесса изменения ЭПР, то интегральный закон (73) определяет относительную долю интервала наблюдения, когда ЭПР будет меньше заданного значения.
Разность 1 - F(SЭ) определяет вероятность того, что случайная величина будет больше заданного значения.

Например,
из рис. 29 найдём F(1)
= 0,63, F(2)
= 0,86, соответственно 1- F(1)
= 0,37, 1- F(2)
= 0,14. Таким образом, в течение 37% времени
наблюдения будет выполняться соотношение
SЭ
≥
![]() и только в течение 14% времени наблюдения
SЭ
≥ 2
и только в течение 14% времени наблюдения
SЭ
≥ 2![]() .
.
