16

Руководство к выполнению лабораторной работы

Составитель: Кречетов А.Д.

ИССЛЕДОВАНИЕ КОРРЕЛЯЦИОННЫХ СВОЙСТВ СИГНАЛОВ

И ФЛЮКТУАЦИОННЫХ ПОМЕХ

Сведения из теории.

Одномерная плотность вероятностей случайного процесса характеризует статистически этот случайный процесс в один фиксированный момент времени и не содержит сведений о поведении случайного процесса в какой – либо другой момент времени. Более полные сведения о случайном процессе даёт двумерная плотность вероятностей p[x(t₁) ,x(t₂) ] , которая позволяет вычислить совместную вероятность того , что значение случайного процесса приt₁находится в пределах отx(t₁) доx(t₁) +dx(t₁) , а приt₂- в пределах отx(t₂) доx(t₂) +dx(t₂). Фиксируяx(t) в момент времениt₁ по функцииp[x(t₁) ,x(t₂) ] , можно найти плотность вероятности любого значенияx(t) в момент времениt₂, т.е. с помощью двумерной плотности вероятностей можно установить наличие и величину статистической связи между значениями случайного процесса в два момента времени.

Часто интересуются лишь линейной статистической связью между значениями процесса. Мерой линейной статистической связи между значениями одного и того же случайного процесса в два различных момента времени служит функция автокорреляции [ 1 , 2 ] , определяемая путём усреднения по ансамблю

(1)

где m(t₁) ,m(t₂) - средние по ансамблю значения процесса в моменты времениt₁ и t₂ соответственно.

Аналогично линейная статистическая связь между двумя процессами x(t) иy(t) в два момента времени характеризуется функцией взаимной корреляции

(2)

Если рассматриваемые процессы стационарные или стационарно – связанные, то средние значения m(t₁) ,m(t₂) (аналогичноm_x(t₁) ,m_y(t₂) ) не зависят от времени, а корреляционные функции (1 ) и (2) будут зависеть лишь от величины=t₂ -t₁ .

(3)

(4)

Для стационарных случайных процессов, обладающих эргодическим свойством, среднее по ансамблю равно среднему по времени, и вычисление корреляционных функций таких процессов можно производить путём усреднения по времени

(5)

Свойства корреляционных функций.

1. Значения автокорреляционной функции большинства случайных процессов убывают с ростом аргумента . Максимального значения автокорреляционная функция достигает при= 0, и оно равно дисперсииK_x ( 0 ) =² по определению. Часто используются понятия времени или интервала корреляции₀ , определяемые из условия, что при₀ [k() /k(0) ] становится меньше заданной величины, например, меньше 0,05. При₀ процессы обычно считают некоррелированными (рис. 1 ).

Рис. 1

2. Корреляционная функция K_y () суммы стационарных случайных процессовx_i(t), гдеi= 1 , 2 , . . . ,n, определяется формулой

(6)

где - автокорреляционная функция процессаx_i(t) ;

- взаимно корреляционная функция процессов x_i(t) иx_j(t).

Если процессы x_i(t) иx_j(t) ,ijне коррелированны, то формула (6) упрощается

(7)

2. Автокорреляционная функция периодического процесса периодична и имеет такой же период, как и исходный процесс. Например, имеется случайный процесс

x ( t ) = cos(₀t +  ), (8)

где ₀ - несущая частота ( известна ) ;

 - начальная фаза ( является случайной величиной, равномерно распределённой на интервале 2,p() = 1 / 2при -).

Для этого процесса, обладающего свойством эргодичности,

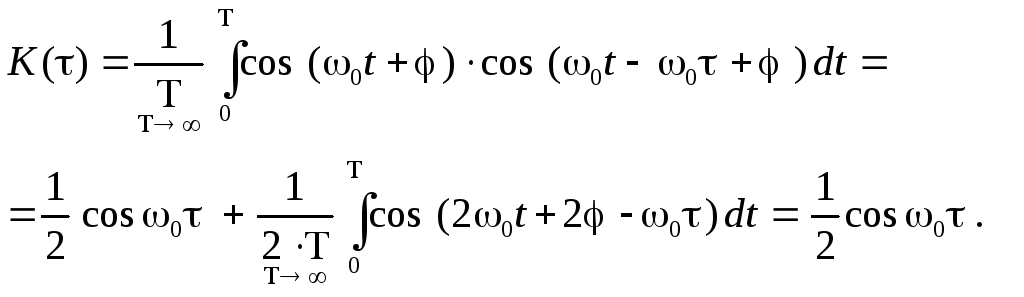(9)

Мы видим, что в данном случае автокорреляционная функция с ростом не стремится к нулю, а её значения меняются с частотой₀ - частотой изменения исходного сигнала. Этот факт можно использовать для обнаружения слабого периодического сигнала на фоне флюктуационной помехи, автокорреляционная функция которой спадает практически до нуля с ростомпри₀. Действительно, если имеется сумма независимых между собой периодического сигналаx(t) и шумаn(t) :y(t) =x(t)+n(t) , то автокорреляционная функция суммы согласно (7)

причём K_n() при_0n, где_0n - интервал корреляции шума, приближённо равна нулю. Следовательно,

Ответ на вопрос о наличии или отсутствии в колебании y(t) периодического сигналаx(t) можно получить из анализа корреляционной функцииK_y() . Если при_0n корреляционная функция периодична, то вy(t) присутствует сигнал и можно даже определить частоту сигнала, сравнивая (8) и (9).

2. Понятие корреляционной функции распространяется и на детерминированные (неслучайные) сигналы.

Значения корреляционных функций зависят не только от величины статистической связи между случайными процессами, но и от величины дисперсий этих процессов. Поэтому для количественной характеристики линейной статистической связи случайных функций вводятся нормированные авто – и взаимнокорреляционные функции

(10)

(11)

называемые также коэффициентами авто- и взаимной корреляции соответственно.

Свойства коэффициента автокорреляции :

1. свойство чётности : R (  ) = R ( -  ) ;

2. абсолютное значение R() при любомне может превышать значения

R(0) = 1;

3) для большинства практически интересных стационарных случайных процессов

Коэффициент взаимной корреляции не обладает этими свойствами. Заметим, что R_xy() =R_yx( -).

Стационарные случайные функции x(t) иy(t), для которых коэффициент взаимной корреляцииK_xy() равен нулю при любом значении, называются некоррелированными, т.е. линейно независимыми. Для коэффициента корреляции также применимо понятие интервала корреляции₀.

Экспериментальное определение функции корреляции эргодического случайного процесса основывается на формуле (5) , причём интегрирование производится по конечному промежутку времени T-.

(12)

Обычно T, и формула (12) упрощается

(13)

Функциональная схема коррелометра - устройства для измерения корреляционной функции - в соответствии с (13) приведена на рис. (2).

Рис. 2.Функциональная схема коррелометра.

Среднеквадратичная погрешность _ измерения функции корреляции нормальных случайных процессов, возникающая из-за конечности времени усреднения Т, определяется [ 3 ] соотношением

(14)

где ₀ - интервал корреляции.

Это соотношение позволяет оценить точность, с какой выполняется тот или иной эксперимент. За ₀берётся такое значение, при котором К (₀) можно пренебречь по сравнению с К(0).

В тех случаях, когда интервал корреляции ₀ представляет очень малую величину, возникает трудность непосредственного определения К(). Тогда используют взаимосвязь между спектральной плотностью мощностиG(f) (энергетическим спектром) стационарного случайного процесса и корреляционной функцией для определения последней. Эта связь даётся преобразованиями Фурье

(15)

(16)

В соответствии с (15) и (16) , чем шире энергетический спектр случайного процесса, тем быстрее с ростом  спадает К().

Так, например, корреляционная функция белого шума, спектральная плотность которого равномерна на всех частотах, представляет собой - функцию.

Если же взять два узкополосных случайных процесса с различной шириной энергетического спектра, то получим корреляционные функции с различным интервалом корреляции (рис. 3).

Рис. 3. Корреляционная функция двух узкополосных случайных процессов с различной шириной энергетического спектра.

Интервал корреляции внутриприёмного шума приблизительно равен величине, обратной полосе пропускания приёмника,

f₀1. (17)

Корреляционные функции широко используются для описания сигналов и помех.

При выборе вида сигнала, используемого в радиосистеме, с помощью автокорреляционной функции сигнала оцениваются точность и разрешающая способность системы по дальности и скорости (т.е. по временному положению и частотеF). Обычно анализируют модуль нормированной совместной (поиF) автокорреляционной функции модуляции используемого сигнала

(18)

называемой функцией неопределённости, где

- энергия сигнала ; u(t) - комплексная амплитуда сигнала.

Функция (18) показывает относительную величину отклика оптимального фильтра на сигнал, сдвинутый по времени на и по частоте наF. Функция

 R(,F)позволяет оценить все характеристики сигнала, определяющие его выбор. Совместная разрешающая способность по задержкеи сдвигуFнесущейf₀определяется формой поверхностиR(,F)(в основном формой главного максимума), величиной и расположением побочных максимумов (боковых лепестков). Точность измерения скорости и дальности в радиолокации зависит от крутизны спадания поверхности главного лепестка по осямиF.

Рис. 4. Функция неопределённости прямоугольного радиоимпульса

длительностью .

На рис. 4 представлена функция неопределённости прямоугольного радиоимпульса длительностью _u .

Понятие функции неопределённости распространяется как на одиночные сигналы, так и на их последовательности. В импульсной радиолокации обычно принимается от цели не одиночный сигнал, а пачка отражённых сигналов, состоящая из нескольких импульсов. В зависимости от свойств цели и характеристик РЛС амплитуды импульсов в пачке могут флюктуировать.

Различают :

1. сигналы с некоррелированными флюктуациями амплитуд, если амплитуды от импульса к импульсу меняются независимо (рис. 5, а ) и коэффициент

корреляции между амплитудами двух соседних импульсов равен нулю

(R_{i j}= 0);

2. частично коррелированные по амплитуде флюктуирующие сигналы, если коэффициент корреляции для двух соседних импульсов не равен нулю

( 0  R _{i j}  1)(рис. 5, б) ;

3. полностью коррелированные флюктуирующие пачечные сигналы, если внутри пачки амплитуды импульсов равны, т. е. R_{i j}= 1 , а от пачки к пачке амплитуды флюктуируют (рис. 5, в).

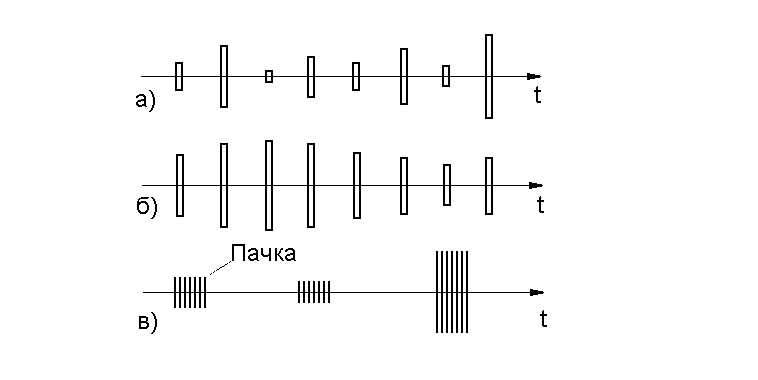Рис. 5

При обнаружении сигналов цели на фоне ряда помех предпочтителен приём сигнала с некоррелированными флюктуациями амплитуд, поэтому применяются методы разрушения корреляции, например, изменения частоты передатчика от импульса к импульсу. Пассивная помеха характеризуется кратковременным и череспериодным коэффициентом корреляции.

Кратковременный коэффициент корреляции вычисляется по одной зафиксированной реализации пассивной помехи, имеет интервал корреляции ₀, приблизительно равный длительности зондирующего сигнала_u. Действительно, при распространении энергии зондирующего сигнала вдоль отражающей поверхности в течение времени, равного_u, происходит полная смена всех элементарных отражателей, и сигналы, отражённые от участков, отстоящих по дальности на, а по времени на_u, оказываются статистически независимыми, т.е.R(_u ) = 0.

Череспериодный коэффициент корреляции характеризует статистическую связь огибающих пассивной помехи, взятых для одной и той же точки дальности в соседние периоды повторения. Значения череспериодного коэффициента корреляции пассивной помехи изменяются значительно медленнее, чем кратковременного. Интервал корреляции ₀в этом случае составляет несколько десятков миллисекунд и, конечно, зависит от свойств отражающей поверхности и вида применяемого сигнала.