1.9. Теоретические законы распределения

Как уже указывалось, функции f(x), F(x), P(x) и (x) полностью характеризуют распределение случайной величины. Обычно эти функции задаются аналитическими выражениями (формулами). Существует несколько таких основных типов формул и соответствующих им типов распределений. В рамках одного типа распределения могут отличаться друг от друга параметрами. Для задания распределения случайной величины необходимо указать как тип, так и параметры распределения. Если у двух случайных величин совпадают и тип распределения, и параметры, то говорят, что они одинаково распределены. Рассмотрим основные распределения, встречающиеся в теории надежности.

1.9.1. Закон нормального распределения (закон Гаусса)

Этот закон является одним из наиболее распространенных законов распределения погрешностей. Уравнение кривой нормального распределения имеет следующий вид:

. (1.25)

Функция распределения имеет вид:

. (1.26)

График плотности нормального распределения называется нормальной кривой или кривой Гаусса (рис.1.14). Отметим смысл характеристик этой кривой:

• –центр группирования, характеризует распределение размеров;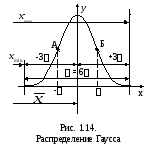

• 

   –характеризует кучность распределения размеров (погрешностей) около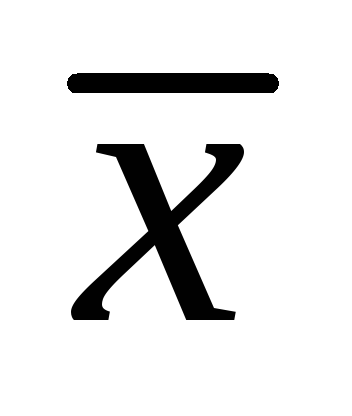 ; чем меньше s, тем кучнее распределяются размеры около .

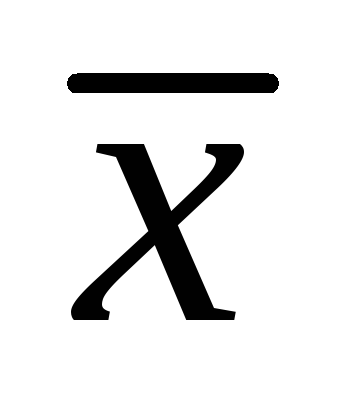Кривая Гаусса имеет следующие особенности.

1. Кривая симметрична относительно .

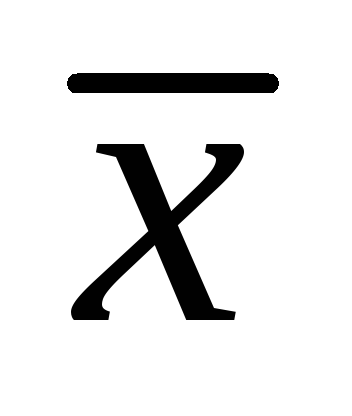2. При 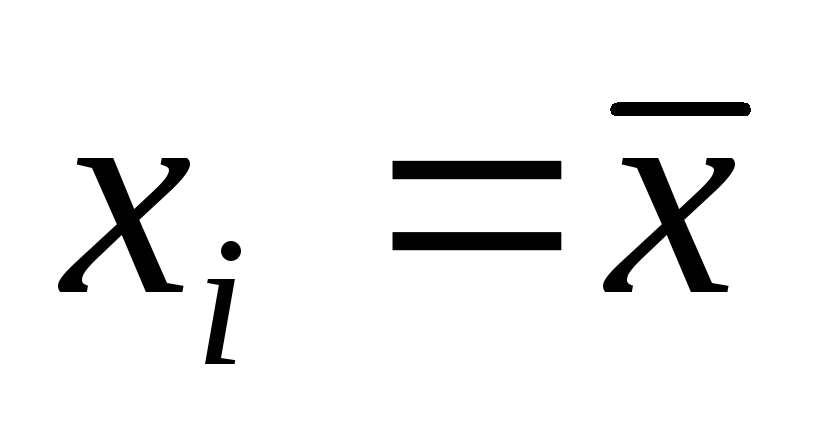, кривая имеет максимум, равный:.

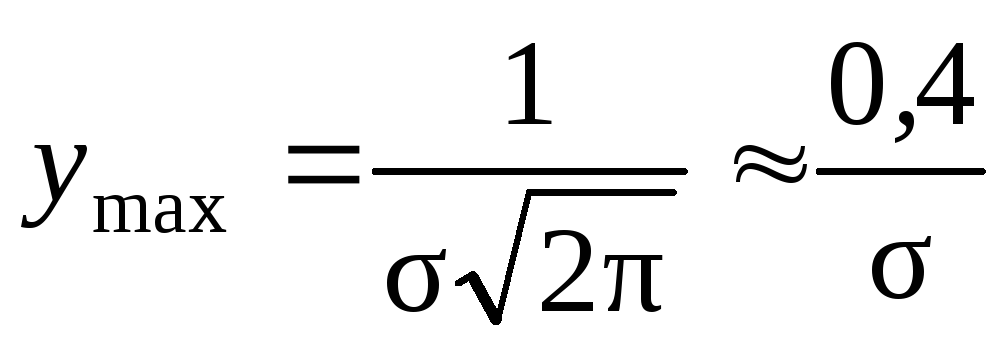3. На расстоянии ± σ от вершины кривая имеет две точки перегиба А и Б, координаты которых равны: .

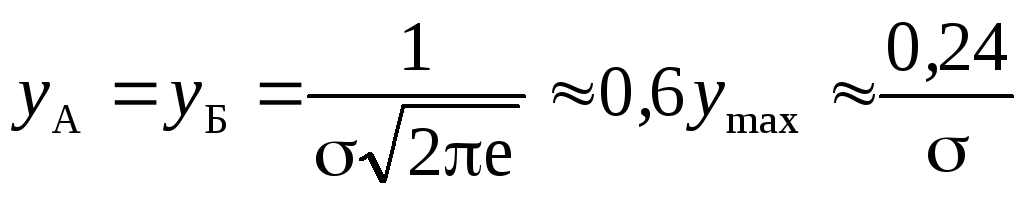4. На расстоянии ± 3 σ от вершины кривой ее ветви так близки к оси абсцисс, что в пределах ± 3σ 99,73 % всей площади ограничивается кривой. Практически принято считать, что на расстоянии ± 3 σ от вершины кривой ее ветви пересекаются с осью абсцисс и в этих пределах заключена вся площадь кривой, т.е. 100,0 %. Погрешность в этом случае составляет 0,27 %, что допустимо при решении многих задач производства.

5. 

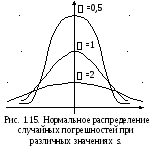
   σ – это мера рассеяния, мера точности. При различных значениях средних квадратических отклонений кривые Гаусса представлены на рис. 1.15. На основании п.4 справедливо утверждение, что поле рассеяния равно

ω ≈ 6 σ. (1.27)

При определении s по данным непосредственных измерений заготовок и расчетов по формуле (1.10) погрешность определения среднего квадратического, обозначаемого в этом случае буквой S, зависит от общего количества N измеренных заготовок и в отдельных случаях весьма значительно. Учитывая это обстоятельство, для предотвращения воз­мож­ного появления брака целесообразно при использовании формулы (1.27) при­нять соотношение

σ = k_×S,

где k_  коэффициент, учитывающий погрешность определения среднего квадратического; S – среднее квадратическое, определяемое по формуле (1.10). Максимальная погрешность (D S) определения S выбирается по табл. 1.5.

Таблица 1.5

Значения максимальной погрешности  S определения S

N, шт.	S, %	kσ	N, шт.	S, %	kσ
25	42,4	1,40	200	15,0	1,15
50	30,0	1,30	300	12,2	1,12
75	25,0	1,25	400	10,6	1,11
100	21,2	1,20	500	10,0	1,10

В тех случаях, когда поле рассеяния параметров (размеров) превосходит поле допуска (ω > δ), условие обработки без брака не выполняется и брак является возможным.

Вероятный процент брака вычисляется следующим образом. При рассеянии размеров, соответствующих закону нормального распределения Гаусса, оценка точности принимается с погрешностью не более 0,27 %, что все детали партии имеют действительные размеры в пределах поля рассеяния

6 σ = x_max – x_min,

где x_max, x_min – максимальное и минимальное значения параметра (размера). При этом площадь, ограниченная кривой нормального распределения и осью абсцисс, равна единице и определяет 100% заготовок партии. Площадь заштрихованных участков (рис. 1.16) представляет собой количество деталей, выходящих по своим размерам за пределы допуска.

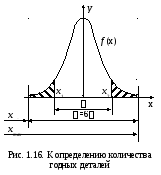
Для определения количества годных деталей необходимо найти площадь, ограниченную кривой и осью абсцисс на длине, равной допуску δ. При симметричном расположении поля рассеяния относительно поля допуска следует найти значение интервала, определяющего половину площади, ограниченной кривой Гаусса и абсциссой х₁ (х₂).

Функция распределения для нормального закона имеет вид:

. (1.28)

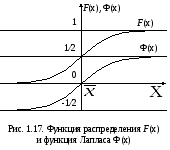
Для случая, когда распределение называют стандартным и функция распределения (1.28) имеет вид (см. рис. 1.17.):

. (1.29)

Таким образом, если случайная величина Х следует закону нормаль­ного распределения, то вероятность появления случайной погрешности определяется площадью, ограниченной кривой f(x) и ее частью и осью абсцисс:

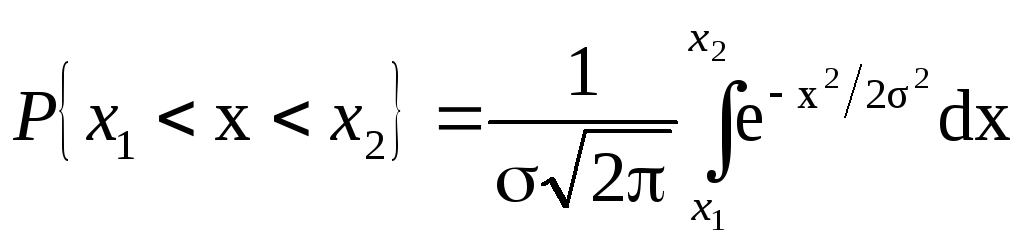. (1.30)

Подынтегральное значение есть элемент вероятности, равный площади прямоугольника с основанием dx и абсциссами x₁ и x₂, называемыми квантилями.

Произведем замену переменной: t = x / s , dx = s×dt

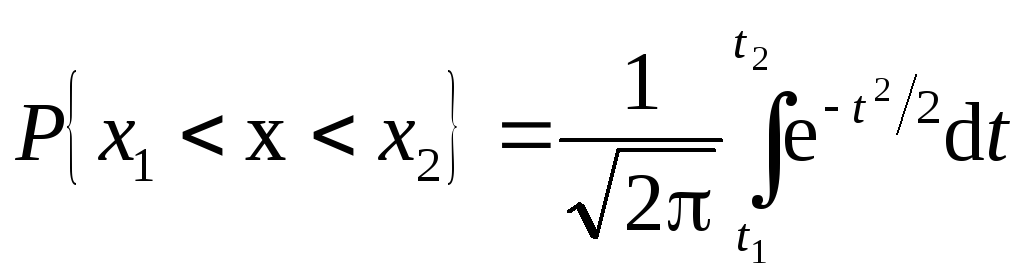. (1.31)

Представим правую часть в виде суммы двух интегралов:

.

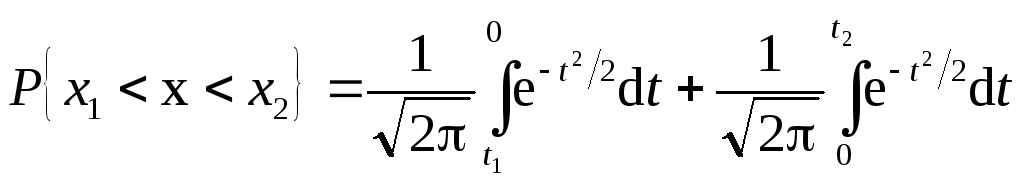Интеграл вида

(1.32)

носит название нормальной функции Лапласа. Значения этого интеграла сведены в табл. (П.3). Таким образом, указанная вероятность (1.30) сводится к разности нормальных функций Лапласа

Р { x₁ < x < x₂ } = Ф (t₂) – Ф (t₁) . (1.33)

Расчет количества годных деталей сводится к установлению величины t и определению Ф(t) по таблице с последующим пересчетом полученных величин в проценты или в число штук изделий.

В общем случае, когда , имеем следующую вероятность появления случайных погрешностей:

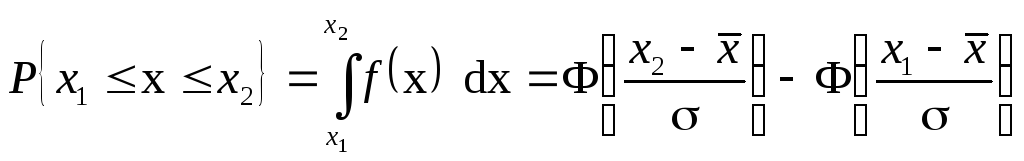. (1.34)

Отметим свойства функции Лапласа: Ф(0) = 0; Ф(–х) = –Ф(х) (функция нечетная); Ф()=1/2. Из рис. 1.17 видно, что кривыеF(х) и Ф(x) эквидистантны.

Если в равенстве (1.34) положить х₁ = –, то

, (1.35)

так как Ф(–}= –Ф()= –1/2. Положив в соотношении (1.34)х₂ =,находим:

. (1.36)

Пример 1.3. При измерении сопротивлений делителя напряжения установлено, что среднее значение этого сопротивления = 5,5 кОм, а среднее квадратическое отклонение = 1,5 кОм. Принимая нормальный закон распределения, найти вероятность появления сопротивлений свыше 10 кОм.

Решение. По равенству (1.36) и из таблиц (П3) находим:

Р(R>10) = 1/2 – Ф[(10 – 5,5)/1,5] = 0,5 – 0,4986 = 0,0014.

Пример 1.4. Определить количество бракованных и годных деталей, если допуск на обработку δ = 0,10 мм. Среднее квадратическое отклонение S = 0,02 (получено по результатам замеров 75 штук). Общее количество обработанных деталей – 300 шт.

Решение. 1. Определяем расчетное значение σ = k_×S = 1,25×0,02 = 0,025 мм.

2. Поле фактического рассеяния ω = 6×σ = 6×0,025 = 0,15 мм превосходит поле допуска δ = 0,1 мм; следовательно, условие обработки без брака не выполнено и появление брака возможно.

3. x = δ/2 = 0,1/2 = 0,05; t = x/σ = 0,05/0,025 = 2,0. Ф(t) = 0,4772, что соответствует 47,72% годных деталей для половины партии. Для всей партии количество годных деталей – 95,44 % или 286 шт., а бракованных 4,56% или 14 шт.

Метод оценки точности на основе кривых распределения универсален и позволяет объективно оценить точность механической обработки, сборочных, контрольных и других операций. Недостаток метода – невозможность выявить изменение изучаемого параметра во времени, т.е. последовательности обработки заготовок, что не позволяет осуществить регулирование хода технологического процесса. Кроме того, переменные систематические погрешности нельзя отделить от случайных; это затрудняет выявление и устранение причин погрешностей. От этих недостатков свободен метод статистического регулирования технологического процесса.