4. Некоторые наиболее важные законы распределения случайных величин

1. Равномерное распределение вероятностей

Для него вероятность того, что с.в. Х попадет в интервал Х:

Prob(Х)=(-)/(b-a).

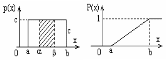
Функция распределения ,a<x<b.

Функция плотности распределения (вероятности):

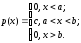
М.о. и дисперсия: .

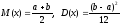2. Нормальное распределение

Плотность распределения: 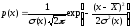(45.4).

Точки перегиба кривой плотности распределения: 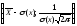и.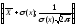

Функция распределения:

(46.4),

где 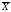- м.о.,(х) – стандарт.

Чем больше (х), тем ниже и шире кривая плотности распределения.

Плотность n-мерного нормального распределения: 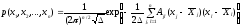, где - определитель корреляционной матрицы , аA_jl – алгебраическое дополнение элемента k_jl-того определителя.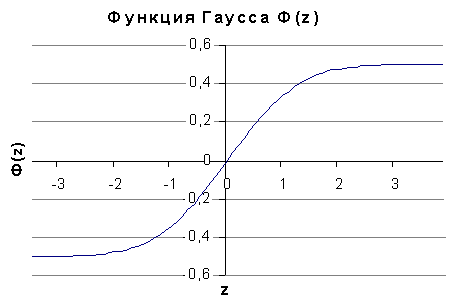

Р(х) можно выразить через интеграл вероятности Гаусса

, (47.4)

(48.4).

Функция (47) – нечетная (Ф(-z) = - Ф(z)), имеются таблицы ее значений.

Вероятность попадания с.в. Х в интервал (a,b) –

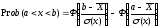(49.4).

Если b-a =6 (X), то вероятность того, что с.в. Х окажется в интервале 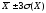равна 0.9973. Линейные функции с.в., подчиняющиеся нормальным законам распределения, имеют также нормальный закон распределения.

Как показал Ляпунов в случае, если число n безгранично увеличивается, кривая плотностей вероятностей суммы не зависит от кривых плотностей вероятностей, слагаемых при некоторых предположениях, и представляет собой нормальную кривую (45.4).

Условия: слагаемые величины х=х₁+х₂+...+х_n (x_i, i=1, 2...n) в среднем одного порядка и одного порядка некоторые характеристики слагаемых - вторые и третьи моменты. Т.о. если с.в. образуется из суммы большого числа независимых, неограниченных случайных переменных факторов, то ее закон - близок к нормальному, т.е. в действительности многие переменные представляют собой результат простого суммирования многих независимых факторов.

Закон больших чисел:

.

3. Усеченный нормальный закон

Если известны границы возможных значений с.в. (a,b), то

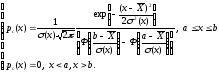(50.4).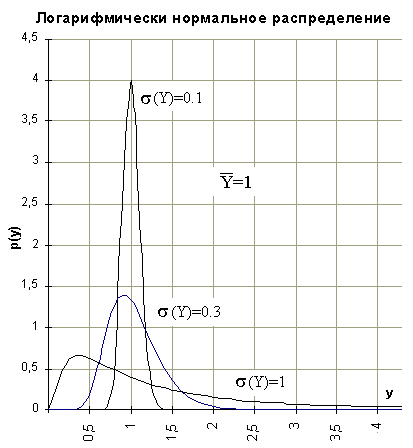

Закон используется для описания реальных величин, распределенных нормально (например, не могущих принимать отрицательные значения).

4. Логарифмически нормальное распределение

Если некоторая с.в. Х распределена по нормальному закону (45.4), то ее экспоненциальная функция

Y=exp(X) (51.4)

(X=ln(Y)) распределится по закону (используем (40.3)):

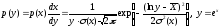(52.4).

М. о. и дисперсия:

, (53.4).

Коэффициент вариации: 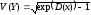. ИзменениюХ по нормальному закону (45.4) в пределах (-,) соответствует изменение Y по закону (52) в пределах (0,+).

5. Распределение Вейбулла

В теории хрупкого разрушения и других отраслях техники нашло применение распределение Вейбулла. Интегральная кривая распределения:

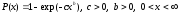(54.4).

Плотность распределения:

(55.4).

В выражения для числовых характеристик распределения Вейбулла входит гамма-функция

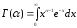(56.4),

которая табулирована в математических справочниках.

6. Распределение Гумбеля (двойное экспоненциальное распределение)

Используется при статистическом анализе снеговых и ветровых нагрузок на сооружения. Функция распределения (интегральная):

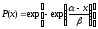(57.4)

Значению x= соответствует вероятность непревышения , равная

P()=exp(-exp0))=exp(-1)=1/e=0.36788.

Значению x=0 соответствует вероятность непревышения 0, равная P(0)=exp[-exp(/)].

Плотность распределения:

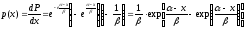(58.4).

В (58) ‑<x<, ‑<<, >0.

Если возвести в n-ную степень (57), то интегральная кривая не изменит своего вида, а только сместится вдоль оси на величину ln(n):

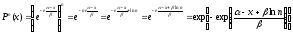(59.4).

Параметры  и  связаны с м.о. и дисперсиейD(x):

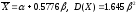(60.4).