
- •Шумилов к. А. Козлова е. М. Вероятностные методы в строительной механике
- •Часть 1
- •Оглавление
- •Задачи теории вероятностей в строительстве. Понятие надежности и ее свойства
- •Основные положения теории вероятностей используемые для решения задач теории надежности строительных конструкций
- •3. Характеристики распределения случайных величин
- •3.1 Одномерная случайная величина
- •3.2 Случайная векторная величина двух измерений
- •3.3 Числовые характеристики распределения системы двух случайных величин
- •Некоторые наиболее важные законы распределения случайных величин
- •4.7 Распределение максимумов случайных величин
- •5. Случайные функции
- •5.1 Характеристики случайных функций
- •5.2. Выбросы случайной функции за заданный уровень
- •Подстановка (82) и (81) в (80) даст для временной плотности вероятности выброса
- •В случае нестационарной функции
- •6. Приближенные методы нахождения распределения функций с.В.
- •7. Вероятность редких событий (появление случайного события a за время t)
- •8. Простейшие модели надежности
- •8.1 Последовательное соединение элементов
- •8.2 Параллельное соединение элементов
- •Литература
- •Приложение
3.3 Числовые характеристики распределения системы двух случайных величин
М.о.
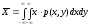 ,
, (32.3)
(32.3)
или
в общем виде
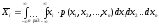 (32.3).
(32.3).
Геометрически
точка
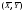 является проекцией на плоскостьXOY
центра тяжести объема, ограниченного
поверхностью распределения p(x,y).
является проекцией на плоскостьXOY
центра тяжести объема, ограниченного
поверхностью распределения p(x,y).
Дисперсия:
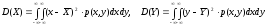 (33.3).
(33.3).Корреляционный момент с.в. X и Y:
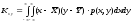 (34.3).
(34.3).
Корреляционный
момент характеризует стохастическую
зависимость между с.в. а также рассеивание.
Корреляционный момент - м.о. произведения
отклонений двух с.в. от их мат. ожиданий
 ,
при
,
при .
.
Корреляционный момент - достоверная величина.
Если зависимости между X и Y нет, то Kxy=0, но из того, что Kxy=0 не следует независимость X и Y.
С.в. могут быть:
1) Независимы, т.е. не коррелированы Kxy=0;
2) Зависимы и коррелированы Kxy0;
3) Зависимы и не коррелированы Kxy=0 (если поверхность плотности распределения симметрична относительно осей координат OX и OY, т.е. M(X)=M(Y)=0).
Коэффициент корреляции:
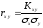 ,
(35.3)
,
(35.3)
где
 - стандарт.
- стандарт.
-1 rxy 1 - характеризует степень тесноты линейной зависимости между с.в. rxy=1 при Y=aX+b (линейная функциональная стохастическая связь).
При нелинейной функциональной связи rxy<1. При отсутствии стохастической связи rxy=0 - необходимое, но недостаточное условие независимости X и Y.
Систему n
с.в. можно охарактеризовать n
м.о.
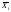 ,n
дисперсиями
,n
дисперсиями
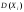 иn(n-1)
корреляционными моментами KXiYj
с i
j
(при этом KXiYj=KXjYi).
иn(n-1)
корреляционными моментами KXiYj
с i
j
(при этом KXiYj=KXjYi).
Функции случайных величин
Функция с.в. будет также случайной величиной Y=(X). Ее распределение соответствует распределению аргумента, но с измененной шкалой абсцисс. P(y)=Prob(Y<y)=Prob((X)<y).
 (36.3)=(17.3),
(36.3)=(17.3),
где (y) - функция обратная (х) (замена подинтегрального выражения x=(y), dx=(y)dy).
Если Y=(X), где (X) - монотонная функция своего аргумента, то распределение Y определяется тем, что вероятность нахождения y в пределах y1<Y<y2 равна вероятности неравенства х1<X<x2,
где y1=(x1) и y2=(x2).
М.о. и дисперсия с.в. Y:
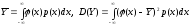 (37.3)=(20.3) и
(22.3).
(37.3)=(20.3) и
(22.3).
Доказательство
(37.3):

Для линейной функции Y=aX+b из (37.3) и (18.3) следует
 и D(Y)=a2D(X)
(38.3).
и D(Y)=a2D(X)
(38.3).
Доказательство
(38):
 .
.
Для функции Z=(X,Y)
двух случайных аргументов м.о. и дисперсия
 (39.3).
(39.3).
Если Z=(X,Y)=X+Y
и X
и Y
- независимы, то м.о.
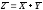 и
дисперсия суммы независимых с.в. величинD(Z)=D(X)+D(Y).
и
дисперсия суммы независимых с.в. величинD(Z)=D(X)+D(Y).
Плотность распределения непрерывной с.в. Y, связанной монотонной функциональной зависимостью Y=(X) с непрерывной с.в. Х:
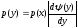 или
или
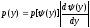 (40.3),
(40.3),
где x=(y) - функция обратная y=(x).
Для линейной функции y=ax+b из (40) следует
p(y)=(1/a)p(x) (40.3).
Если Y=(X/R)
и p(x/r)
- условная плотность вероятности с.в.
Х,
входящей в систему (X,R),
то условная плотность вероятности с.в.
Y
-
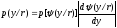 ,
,
где (y/r) - функция обратная Y=(X/R), а безусловная плотность вероятности с.в. Y:
 ,
,
где p(r) - плотность вероятности с.в. R.
Если имеются функции с.в. U=U(X,Y) и V=V(X,Y), то, зная совместную плотность распределения p(x,y), совместная плотность распределения U и V:
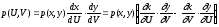 (41.3)
(41.3)
(в
скобках - Якобиан
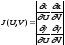 ).
).
Матожидания:
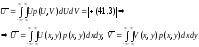 (42.3),
(42.3),
дисперсия
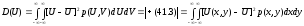 ,
,
корреляционный
момент
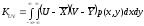 .
.
В случае линейного
преобразования U=a1X+b1Y+c1
и V=a2X+b2Y+c2
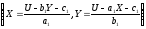 по (41.3) и (42.3) имеем:
по (41.3) и (42.3) имеем:
 (43.3),
(43.3),
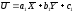 и
и
 (44.3).
(44.3).
Дисперсия
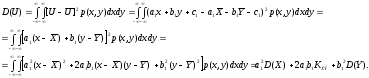
Доказательство (44)
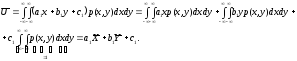
Запишем еще раз дисперсии и корреляционные моменты:
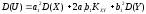 ,
,
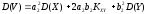 ,
,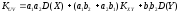 (доказать самостоятельно).
(доказать самостоятельно).
Зная плотность
распределения p(U,V),
где U=U(X,Y)
и V=V(X,Y),
можно определить плотность распределения
p(U)
или p(V):
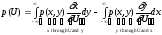 .
.
Пример (стр.23 [7]). Стержень нагружен изгибающим моментом Mb и крутящим моментом Mt, и есть их совместная плотность вероятности pq(Mb,Mt). Кроме того, моменты Mb и Mt стохастически независимы и подчиняются центрированному нормальному распределению:
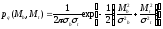 ,
,
где b и t – стандарты Mb и Mt.
Опасное состояние
стержня достигается при превышении
некоторой функцией этих моментов
предельного значения Mr>Mr,lim,
зависящего от свойств материала и
геометрии сечения стержня. Например,
для стержня круглого сечения из
пластического материала эта функция
может быть взята в виде
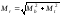 ,
гдеMr
– приведенный момент, определенный в
соответствии с критерием текучести,
основанном на наибольших касательных
напряжениях.
,
гдеMr
– приведенный момент, определенный в
соответствии с критерием текучести,
основанном на наибольших касательных
напряжениях.
Касательное
напряжение от крутящего момента
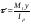 ,
гдеI
- полярный момент круглого сечения, y
– радиус окружности, содержащей
рассматриваемую точку,
= max
при y=r
(r
– радиус стержня). Нормальное напряжение
от изгибающего момента
,
гдеI
- полярный момент круглого сечения, y
– радиус окружности, содержащей
рассматриваемую точку,
= max
при y=r
(r
– радиус стержня). Нормальное напряжение
от изгибающего момента
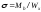 .
Для расчета надежности стержня необходимо
знать плотность вероятностиpu(Mr)
приведенного момента Mr.
.
Для расчета надежности стержня необходимо
знать плотность вероятностиpu(Mr)
приведенного момента Mr.
Перейдем к полярным
координатам, положив
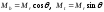 ,
где 02.
Согласно (41.3) совместная плотность
распределения с. в. Mr
и :
,
где 02.
Согласно (41.3) совместная плотность
распределения с. в. Mr
и :
 .
.
Используя
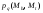 и замечая, что якобиан преобразования
и замечая, что якобиан преобразования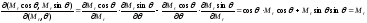 ,
,
найдем

Плотность
распределения вероятности pu(Mr)
определяется интегрированием полученной
формулы по углу :
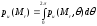 .
Используя формулу анализа
.
Используя формулу анализа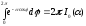 ,
где
,
где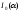 - функция Бесселя мнимого аргумента
нулевого порядка, получим окончательно
- функция Бесселя мнимого аргумента
нулевого порядка, получим окончательно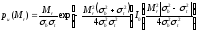 .
.
Если дисперсии
моментов Mb
и Mt
одинаковы, т.е. b=t=,
то I0(0)=1
и
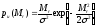 .
При этом приведенный момент подчиняется
распределению Рэлея.
.
При этом приведенный момент подчиняется
распределению Рэлея.
