Анықталмаған интегралдар кестесі:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

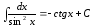
15.

16.

17.

18.

19. [2].

Интегралды табуда мынадай жағдайларды ескеру керек:

1. Интегралды табуды тікелей кестелік интегралды пайдаланып есептеуге болады.

2. Анықталмаған интегралдың қасиеттерін пайдалану нәтижесінде интегралды есептеуді бір немесе бірнеше кестелік интегралдарды есептеуге алып келуге болады.

3. Интеграл таңбасы астындағы функцияны түрлендіру және интеграл қасиеттерін пайдалану нәтижесінде бір немесе бірнеше интегралдар есептеуге тура келеді.

Егер болса, ондаорындалады.

Мұнда аргументі жаңааргументімен ауыстырылған. Интеграл берілген күйінде кестелік интегралға келмейтін кезде көптеген жағдайларда, интеграл астындағы өрнекті түрлендіру арқылы оны кестелік интегралға келтіруге болады. Мұндай жағдайда қандай түрлендіру жүргізу керек екенін білу қажет.

Егер интеграл түрінде беріліп,теңдігі орындалса, онда интегралды кестелік интегралға келтіруге болады, яғни

4. Анықталмаған интеграл. Бөліктеп интегралдау әдістері. Рационалды функцияларды интегралдау. Тригонометриялық функцияларды интегралдау. Анықталған интеграл және оның қасиеттері.

Дифференциалдау мен интегралдау амалдары өзара кері амалдар. Функцияның алғашқы функциясын табу операциясын интегралдау деп атайды.

Анықтама: Кез келген жиынында өзгеретінүшінтеңдігі орындалса ондафункциясынфункциясының алғашқы функциясы дейді.

Алғашқы функция анықтамасын қолданып есептер шығаруға мысалдар қарастырайық:

1-есеп:

функциясы аралығындафункциясы үшін алғашқы функция болатынын көрсетейік.

теңдігін қолдансақ:

мұндағы ; дәлелдеу керегі осы болатын.

2-есеп: функциясы үшін графигінүктесі арқылы өтетін алғашқы функцияны анықтаңыз.

Шешуі: функциясы үшін алғашқы функцияболады.

Себебі 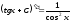(1) теңдіккемәндерін қойып:

теңдеуінен С мәнін анықтаймыз.

. Сонымен алғашқы функция болады.

Анықтама: функцияларының барлық алғашқы функцияларының жиынтығыберілген функциясының анықталмаған интегралы деп аталады.

Мынадай түрде жазылады:

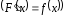(1)

Мұндағы - интегралдау белгісі,х –интегралдау айнымалысы, –ті интеграл таңбасы астындағы функция, ал- интеграл таңбасы астындағы өрнек дейді,- алғашқы функцияның жалпы түрі,- кез келген тұрақты сан,-тің дифференциалы.

Есептерді шешуде функциясы бойынша алғашқы функциялардыңжалпы түрін табу қойылады.–ты негізгі алғашқы функция дейді.

Анықталмаған интегралдың қасиеттері:

1. -тұрақты сан.

2.

3.

4. [1].

Бөліктеп интегралдау

осы көбейтудің дифференциалының формуласын екі жағын интегралдап, келесі бөліктеп интегралдау формуласын аламыз:

Бұл формулада интегралын зерттеуде мынаинтегралды есептеуге келеді. Мұнда бастапқы интегралды есептеу соңғы интегралды есептеуден қиынырақ болғандықтан осы формуланы пайдаланып шығарамыз.

интегралын есептеу үшін интеграл астындағы өрнекті u және dv деп белгілеп алу керек. dv ретінде көбінесе туынды алынбайтын функцияларды аламыз, мысалы үшін .

Мысал.

Рационал функцияларды интегралдау

Рационал функциялар әрқашанда элементар функцияларда интегралданады. , мұндажәнеP(x) көпмүшелер, бөлшекті рационал функцияның интегралын барлық уақытта интегралдауға болатын қосылғыштарға жіктеу арқылы табуға болады.

Алымының дәрежесі бөлімінің дәрежесінен үлкен не тең болатын бұрыс рационал бөлшекті алымын бөліміне бөлу арқылы, яғни көпмүшелер мен алымының дәрежесі бөлімінің дәрежесінен кіші болатын дұрыс бөлшектін қосындысы түрінде жазуға болады.

Дұрыс рационал бөлшекті әрқашанда келесі екі интегралданатын бөлшектің қосындысы түрінде элементар бөлшектерге жіктеуге болады:

мұнда m және n –бүтін оң сан.

1. бөлімін қарапайм нақты көбейткіштерге жіктейміз. Жалпы жағвдайда, алгебраның негізгі теоремаларына сүйене отырып, бұл жіктеудің құрамында сызықты және квадраттық көбейткіштер бар болады:

б) Берілген бөлшекті келесідей түрде элементар бөлшектердің қосындысы түрінде жіктей аламыз:

мұнда ,…,,…,,…,,…,,…,,..., -кейбір тұрақтылар. Бұл тәсілде бөлшектің бөліміндегі көбейткіштердің дәрежесіне байланысты сонша элементар бөлшектердің қосындысы түрінде жазылады. Ал бөлшектің алымы бөлімінің сызықты не квадратты функция болатындығына сәйкес тұрақты не сызықты функция болады.

в) Теңдіктің екі бетінде -ке көбейтіп, бөлшек бөлімінен құтыламыз.

г) Енді алымдарының теңдігінен коэффициенттерін теңестіріп, теңдеулер жүйесін аламыз.

д) Жүйені шешіп, табылған коэффициенттерді элементар бөлшектердің қосындысына апарып қоямыз.

Осы алынған элементар бөлшектерді интегралдаймыз. Яғни кез келген дұрыс рационал бөлшекті интегралдауда элементар бөлшектердің қосындысына жіктеуден кейін келесі түрдегі интегралдарды табу керек болады:

және .

кезде интегралы келесідей шығады: