matan27-30 by Erbolat
.docx27. Properties of Function Defined by Power Series.
We know the properties of functions defined by Power series. Henceforth, we consider only power series with non-zero radius of convergence.
Theorem
3.
A power series
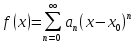 (1) with R>0 is continuous and differentiable in its interval of
convergence, and it's derivative can be obtained by differentiating,
term by term; that is
(1) with R>0 is continuous and differentiable in its interval of
convergence, and it's derivative can be obtained by differentiating,
term by term; that is
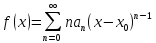 (2) which can also be written as
(2) which can also be written as
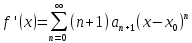 (3)
(3)
This series also has radius of convergence R.
Proof:
First, the series in (2) and (3) are came, since the after is
obtained by shifting the index of summation in the former. Since
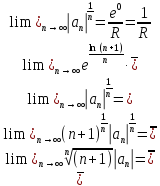
the
radius of convergence of the power series in (3) is R. Therefore,
the power series, in (3) convergence
uniformly
in every interval [x0-r,
x0+r]
such that 0<r<R and (3)
 (x0-R,
x0+R).
(x0-R,
x0+R).
Theorem
4. A
power series
 R>0, has derivative of all orders in it's interval of convergence,
which can be obtained by repeated term by term differentiation, thus
R>0, has derivative of all orders in it's interval of convergence,
which can be obtained by repeated term by term differentiation, thus

Corollary.
If
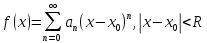 then
then

28. Uniqueness of Power Series
Theorem
5.
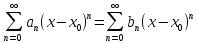 (1) for all x in so me interval (x0-r,
x0+r),
then an=bn
(2)
(1) for all x in so me interval (x0-r,
x0+r),
then an=bn
(2)
Proof:
Let
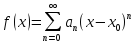 and
and
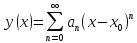
From
corollary ( if
 then
then
 )
)
 and
and
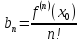 (3)
(3)
From
(1),
 in (x0-r,
x0+r).
Therefore,
in (x0-r,
x0+r).
Therefore,
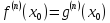 n≥0. This and (3) imply (2).
n≥0. This and (3) imply (2).
Theorem
6. If
x1 and x2 are in the interval of convergence of
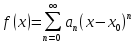 (4) then
(4) then
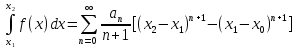 (5) that is a power series may be integrated term by term between
any the points in it's interval convergence.
(5) that is a power series may be integrated term by term between
any the points in it's interval convergence.
29.Taylor's series.
A
function
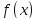 must have derivatives of all orders in some neighborhood(окрестность)
of x0
and the only power series in (x-x0)
can be possibly coverge to such neighborhood is
must have derivatives of all orders in some neighborhood(окрестность)
of x0
and the only power series in (x-x0)
can be possibly coverge to such neighborhood is
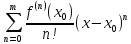 (1)
(1)
This
is called the Taylor's series of
 about
about
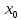 (also Maclouzin series of
(also Maclouzin series of
 if
if
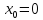 )
)
The n-th partial sum of (6) is the Taylor polynomial

If
 is infinitely differentiable on (a,b) and x and x0
are in (a,b), then for every integer n≥0
is infinitely differentiable on (a,b) and x and x0
are in (a,b), then for every integer n≥0
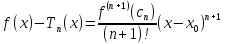 there cn
between x and x0
there cn
between x and x0
 for
all x in (a,b), is iff
for
all x in (a,b), is iff
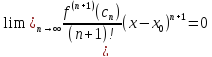
Thorem.
Suppose that
 infinitely differentiable on an interval G and
infinitely differentiable on an interval G and
 (2)
(2)
Then,
if
 the Taylor series
the Taylor series
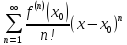 uniform convergence
uniform convergence
 in
in
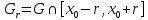
Thorem.
If
 (3)
(3)
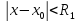
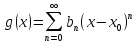 (4)
(4)
 and α and β constants, then
and α and β constants, then
 ,
,
 where
where
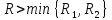
Thorem.
If
 and
and
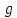 are given by (3)
and (4)
then
are given by (3)
and (4)
then
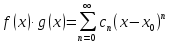 (5)
(5)
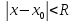 where
where
 and
and
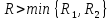
30. Abel's theorem.
We
know that a function
 defined by a convergent power series
defined by a convergent power series
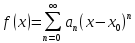 (1)
(1)
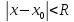 is
continuous in the open interval (
is
continuous in the open interval (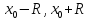 )
)
The
next theorem concerns the behavior(поведение)
of
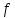 as x approaches an endpoint of the interval of convergence.
as x approaches an endpoint of the interval of convergence.
Theorem Abel's.
Let
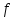 be defined by a power series (1) with finite radius of convergence R
be defined by a power series (1) with finite radius of convergence R
a)
If
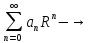 ,
then
,
then
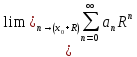
Proof:
We
consider a simpler problem first. Let
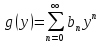 and
and
 (finite) we will show that
(finite) we will show that
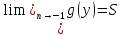 (2)
(2)
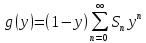 (3),
where Sn=b0+b1+...+bn
(3),
where Sn=b0+b1+...+bn
Since
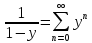 and therefore
and therefore
 (4)
(4)
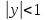 we can multiply through by S and write
we can multiply through by S and write
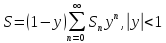 . Subtracting this from (3) yields
. Subtracting this from (3) yields
 .
.
if
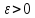 choose N so that
choose N so that
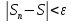 ,
if n>N+1.
,
if n>N+1.
Then, if 0<y<1
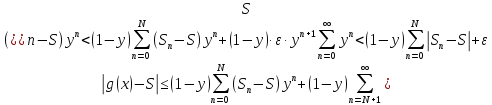 because
of the second equality in (4).
because
of the second equality in (4).
Therefore,
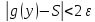 ,
if
,
if
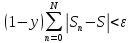 this proves (2).
this proves (2).
to
obtain (a) from this, let
 and
and
 ;
;
to
obtain (b)
 and
and