1.Тізбектер және оның шегі. Жинақты тізбектер және олардың қасиеттері.Тізбек жинақтылығының Коши критериі.

Натурал сандар жиынында анықталған 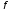функциясының мәндерін сан тізбегі немесе тізбек деп атайды.

Егер 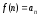тізбегі берілсе, оны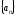символымен белгілейді немесе былай жазад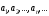ы:

Мысалы, 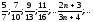тізбектің шегін табу керек.

Шешімі. 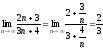болады.

Анықтама. Шегі бар тізбекті жинақты деп, шегі жоқ тізбекті жинақсыз деп атайды. Егер тізбектің шегі бар болса, онда тізбек шектелген болады. Жинақты тізбектің бір ғана шегі бар. Жоғары (төменгі) жағынан шектелген өспелі (кемімелі) тізбектің шегі бар.

Теорема 4. Егер 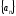және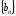тізбектері жинақты болса, онда

1) ;

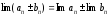2) ;

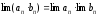3) ;

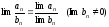4) .

Егер 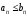, онда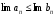

Коши критерийі  

Х_n тізбегі R жиынында жинақты болу үшін Хn тізбегінің фундаментальді болуы қажетті және жеткілікті

Қажеттілік айталық х_nтізбегі жинақты және оның шегі а болсын сонда мұның фундаментальді екенін көрсетейік

∃nϵN=>| x_n-a| =а. Демек n+p>n_a үшін де фундаментальді Хn функционалды тізбек

2. Бір айнымалы функциялар түсінігі. Функциялар шегі

Бір айнымалы ф-я да тәуелсіз айнымалы жалғыз болады. Ф-яға түсінік беріп кетейін: ф-я дегеніміз тәуелсіз айнымалының бір мәніне тәуелді айнымалыныі бір ғана мәні сәйкес келетін бейнелеуді айтады. Бірақ тәуелді айнымалының бір мәніне тәуелсіз айнымалының бірнеше мәні сәйкес келуі мүмкін.

( Eki domalak syzu)

P мен q әріптерінің әрқайсысы c(c-нақты сан) , c+0,c-0, ∞,+∞ және -∞ символдарының бірі, f функциясы X нақты сандар жиынында анықталып, p сол жиынның шектік нүктесі болсын. Егер әрбір ε оң саны үшін f функциясының p- ның белгілі бір ойылған δ(ε)- маңайында қабылдайтын міндердің бәрі де q- дің маңайында жатса, онда x p – ға ұмтылғанда f(x) функциясының шегі бар және q- ға тең дейді де , 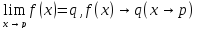немесе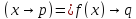символдармен белгіленеді.

Бұл жағдайды басқаша

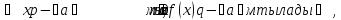
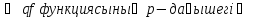деп те атайды.

Дәлірек p=a, p=a+0, p=a-0 болғанда 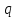-ді f функциясының a нүктесіндегі сәйкес жай (екі жақты) , оң жақты және сол жақты шегі деп, ал q=b, q=b+0, q=b-0 болғанда f функциясы сәйкес b-ға, b-ға жоғарыдан, b-ға төменнен ұмтылады дейді.

Шектің анықтамасы кванторлар тілінде былай жазылады:

Коши критерийі.

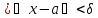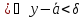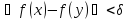f функциясы X жиынында анықталып, a нақты саны сол жиынның шектік нүктесі болсын. Онда f функциясының a нүктесінде нақты мәнді шегі бар болуы үшін, әрбір ε оң саны бойынша X жиынынан алынған 0және 0теңсіздіктерін қанағаттандыратын кез келгенx,y сандары үшін теңсіздігі орындалатындай δ оң саны табылуы қажетті және жеткілікті.

Кванторлар тілінде бұл теорема былай жазылады:

f- тің а нүктесінде нақты ()()()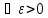

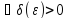мәнді шегі бар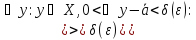

:ε. (1)

(1)- нің оң жағында жазылған шарт Коши шарты деп аталады.

Сонымен Коши критерийін былай айтуға болады: 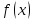функциясының а нүктесінде нақты мәнді шегі бар болуы үшін сол нүктеде Коши шарты орындалуы қажетті және жеткілікті.

3. Үзіліссіз функциялар түсінігі. Үзіліссіз функциялардың арифметикалық операциялары. Элементар функциялардың үзіліссіздігі.

Үзіліссіздіктің анықтамасы жөнінде жалпы ескертулер жасайық.

1.Үзіліссіздіктің анықтамасы келесі екі шарттың орындалуын талап етеді: біріншіден, x x₀-ге ұмтылғанда f(x)-тің y₀ нақты санына шегі бар, екіншіден y₀ саны f функциясының x₀ нүктесінде қабылдайтын мәні болатын f(x₀) санына тең.

2.Үзіліссіздік-локальді ұғым.

3. Жалпы жағдайда функцияның әрбір жеке алынған нүктеге сәйкес мәнінің қалған нүктелерде қабылдайтын мәндерімен ешқандай байланысы жок. Мысалаы:

f(x)=

сәйкестігі функция болады. Сонымен бірге ноль нүктесінде мәні басқа мәндермен ешқандай байланысы жоқ,себебі 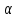=f(0) санына нақты болуынан өзге шарт қойылмаған.

Ал үзіліссіз функция үшін жағдай мүлде басқа: 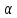нүктесінде f функциясы үзіліссіз болса, онда f(а) саны f функциясының а-ның «қасындағы» нүктелерде қабылдайтын мәндері арқылы табылады. Дәл айтқанда f(а) саны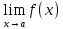шегіне тең, ал сол шектің анықтамасында f функциясының а нүктесінде қабылданатын мәні қатыспайды,тіпті бар болуы да қажетті емес.

4.болғандықтан үзіліссіздіктің анықтамасындағы 1- теңдікті былай да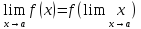жазуға болады.

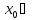5Үзіліссіздіктің x→f(x) →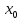түріндегі анықтамасын үзіліссіздіктің x→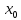символының екі жағын даережесін қолданғанда , сондағы ұмтылу сақталатынын белгілейді деп түсінуге болатынын көрсетеді.

Үзіліссіз функциялар шарттарды қанағаттандырады,сондықтан аталған теоремалардан салдар ретінде үзіліссіз функциялардың келесі маңызды қасиеттері шығады:

1-теорема. Әрбір функцияның үзіліссіздік нүктесі локальді шенелу нүктесі болды.

2-теорема. Егер f функциясы 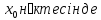үзіліссіз болып, сол нүктеде қабылданған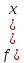) мәні оң (теріс) болса, онда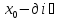белгілі бір маңайындамәндері де оң (теріс) болады.

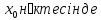Салдар. Егер функциясыүзіліссіз болып,оның белгілі бір ойылған маңайындағы барлық нүктелерде қабылданатын мәні нольге тең болса не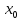-дің кез келген ойылған маңайында оң және теріс таңбалы мәндерді қатар қабылдаса, онда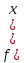)=0 болады.

4. Туынды функция және оның геометриялық, физикалық мағынасы. Қосындыны, айырманы, туынды, бөлікті дифференциалдау ережелері.

Туынды анықтамасы. функциясы І аралығында анықталынсын. Егер x₀ÎІ үшін ақырлы шегі бар болса, онда ол шектіфункциясының x₀ нүктесіндегі туындысы деп, символымен белгілейді.

Туынды табу амалын функцияны дифференциалдау дейді. Сонымен, анықтама бойынша

.

Басқаша сөзбен анықтама былай айтылады: Егер функцияның өсімшесінің өзінің пайда болуына себепші болған тәуелсіз айнымалының өсімшесіне қатынасының соңғы өсімше нольге ұмтылғанда ақырлы шегі бар болса, онда функцияны дифференциалданатын деп, сол шекті функцияның туындысы деп атайды.

Дәл осы сияқты, функциясыныңх₀ нүктесіндегі сәйкес сол және оң жақты туындыларының анықтамасына келеміз:

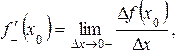
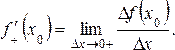
Демек, функциясыныңх₀ нүктесінде туындысы бар болуы үшін, оның ол нүктеде сол және оң жақты туындылары бар болып, олар өзара тең болуы қажетті және жеткілікті.

2. Дифференциалдау ережелері. жәнефункциялары дифференциалданатын, алс түрақты сан болса, онда келесі дифференциалдау ережелері орындалады:

 

1.

2.,

3. ,

4. ,

5. .

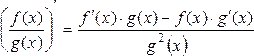
Туындының геометриялық және механикалық мағынасы. функциясыныңх₀ нүктесiндегi туындысының бар болуы, оның графигiнiң нүктесiнде жанаманың бар болуымен бара бар. Бұл жағдайда,жанаманың бұрыштық коэффициентi -қа тең. Туындының геометриялық мағынасы осы.функциясы графигiненүктесiнде жүргiзiлгенжанаманың теңдеуi

болады. нүктесiнен жанамаға перпендикуляр болып өтетiн түзудiфункциясы графигiне, осы нүктеде жүргiзiлгеннормаль деп атайды, оның теңдеуi

болады.

Егер материалдық нүктенiң қозғалыс заңы функциясы арқылы берiлсе, онда оның уақыт бойынша алынған туындысы жылдамдықты, ал екiншi реттi туындысы үдеудi анықтайды. Бұл бiрiншi реттi және екiншi реттi туындының механикалық мағынасы болып табылады.

Мысал. қисығына абсциссасыболатын нүктеде жүргiзiлген жанама мен нормальдiң теңдеуiн жазайық.

Шешуi:Нүктенiң ординатасын табамыз

.

Туындысын анықтайық: ; Сонда жанаманың бұрыштық коэффициентi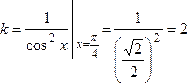болады.

Сонымен, жанаманың теңдеуi , ал нормальдiң теңдеуiболады екен.

4. Бір айнымалы функцияны дифференциалдау. Күрделі функцияларды дифференциалдау ережелері.

Туынды анықтамасы. функциясы І аралығында анықталынсын. Егер x₀ÎІ үшін ақырлы шегі бар болса, онда ол шектіфункциясының x₀ нүктесіндегі туындысы деп, символымен белгілейді.

Туынды табу амалын функцияны дифференциалдау дейді. Сонымен, анықтама бойынша

.

Басқаша сөзбен анықтама былай айтылады: Егер функцияның өсімшесінің өзінің пайда болуына себепші болған тәуелсіз айнымалының өсімшесіне қатынасының соңғы өсімше нольге ұмтылғанда ақырлы шегі бар болса, онда функцияны дифференциалданатын деп, сол шекті функцияның туындысы деп атайды.

Дәл осы сияқты, функциясыныңх₀ нүктесіндегі сәйкес сол және оң жақты туындыларының анықтамасына келеміз:

Демек, функциясыныңх₀ нүктесінде туындысы бар болуы үшін, оның ол нүктеде сол және оң жақты туындылары бар болып, олар өзара тең болуы қажетті және жеткілікті.

функцияларды дифференциалдау

 1. (1)

тепе-теңдiгi кез келген мәндерiнде орындалса, ондафункциясыаралығындаайқындалмаған түрде теңдеуiмен берiлдi дейдi.функциясының туындысын табу үшiн (1) тепе-теңдiктiң сол жағынх айнымалысының күрделi функциясы деп, х бойынша дифференциалдап, алынған өрнектен - тi табу керек.

2. (2)

функциялары берiлсiн.

Егер аралығындафункциясыныңкерi функциясы бар болса, онда

. (3)

Функция (2)-нi параметрлiк қатынастар түрiнде берiлген деп атайды.

Керi функцияның дифференциалдау ережесi бойынша (3) функцияны х бойынша дифференциалдасақ

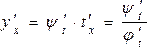
немесе өрнегiн аламыз. Бұл параметрлiк теңдеулер түрiнде берiлген функцияныдифференциалдау ережесi деп аталынады.

4. Алғашқы функция. Анықталмаған интеграл. Анықталмаған интегралдың негізгі қасиеттері.

Дифференциалдау мен интегралдау амалдары өзара кері амалдар. Функцияның алғашқы функциясын табу операциясын интегралдау деп атайды.

Анықтама: Кез келген 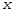жиынында өзгерет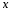інүшін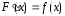теңдігі орындалса ондафункциясын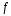функциясының алғашқы функциясы дейді.

Алғашқы функция анықтамасын қолданып есептер шығаруға мысалдар қарастырайық:

1-есеп:

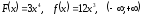
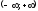функциясы аралығындафункциясы үшін алғашқы функция болатынын көрсетейік.

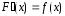теңдігін қолдансақ:

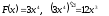мұндағы 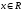; дәлелдеу керегі осы болатын.

2-есеп: функциясы үшін графигі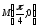нүктесі арқылы өтетін алғашқы функцияны анықтаңыз.

Шешуі: 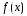функциясы үшін алғашқы функция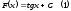болады.

Себебі 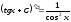(1) теңдікке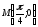мәндерін қойып:

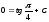теңдеуінен С мәнін анықтаймыз.

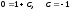. Сонымен алғашқы функция болады.

Анықтама: 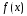функцияларының барлық алғашқы функцияларының жиынтығыберілген функциясының анықталмаған интегралы деп аталады.

Мынадай түрде жазылады:

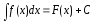
(1)

Мұндағы 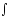- интегралдау белгісі,х –интегралдау айнымалысы, 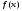–ті интеграл таңбасы астындағы функция, ал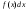- интеграл таңбасы астындағы өрнек дейді,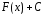- алғашқы функцияның жалпы түрі,- кез келген тұрақты сан,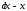-тің дифференциалы.

Есептерді шешуде функциясы бойынша алғашқы функциялардың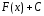жалпы түрін табу қойылады.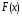–ты негізгі алғашқы функция дейді.

Анықталмаған интегралдың қасиеттері:

1. 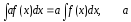-тұрақты сан.

2.

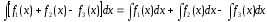
3.

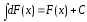
4. 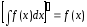[1].