Событие наз. случайным, если оно может появится или не появится при данном комплексе условий.

Событие называется достоверным, если при заданном комплексе условий оно обязательно наступает. Все достоверные события обозначаются буквой U.

Событие называется невозможным, если при заданном комплексе условий оно наступить не может. Все невозможные события обозначаются буквой V.

События А1,А2,…,Аn называется несовместными, если появление одного из этих событий исключает появление любого другого в одном и том же испытании.

События А1,А2,…,Аn называются единственно возможными, если при реализации заданного комплекса условий обязательно должно наступить хотя бы одно из этих событий.

События А1,А2,…,Аn образуют полную группу событий, если эти события единственно возможные и несовместные.

Два события і , образующие полную группу, называются противоположными.

События А1,А2,…,Аn называются равновероятными или равновозможными, если при проведении испытания все они объективно имеют одинаковую возможность на появление.

Простір елементарних подій – усі єдино можливі, рівноможливі та несумісні події, які неможливо поділити на більш прості події.

Імовірність події A дорівнює: P(A)= m/n

де n - число (кількість) подій у просторі елементарних подій,

а m - число наслідків (із простору елементарних подій), які сприяють появі події A.

Означення. Нехай проводиться n випробувань (які можна повторювати при незмінних умовах необмежено). Частотою m(A) називається кількість випробувань (із n), в яких з’явилась подія A. Частістю (відносною частотою або

1. Означення. Імовірність події дорівнює:

де - число (кількість) подій у просторі елементарних подій,

а - число наслідків (із простору елементарних подій), які сприяють появі події .

Властивості:

1. Для довільної події : ;

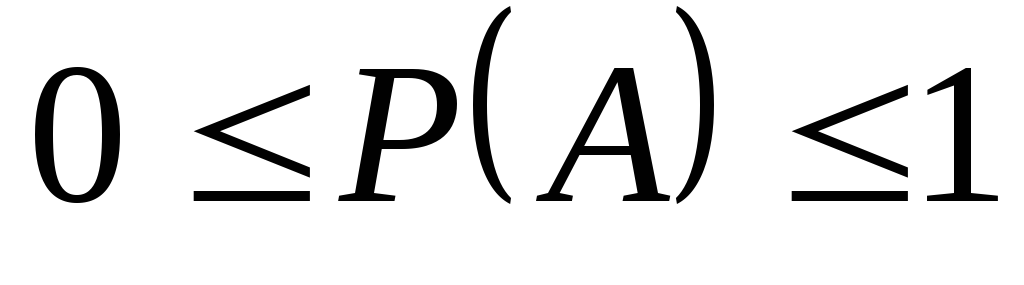2. Для достовірної події : .

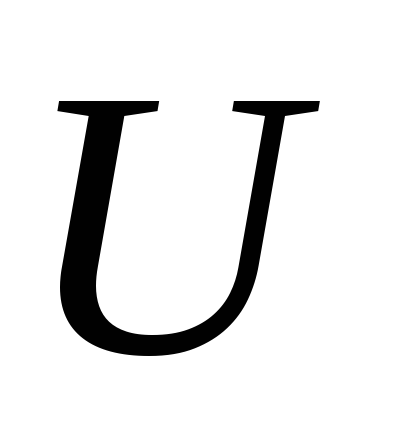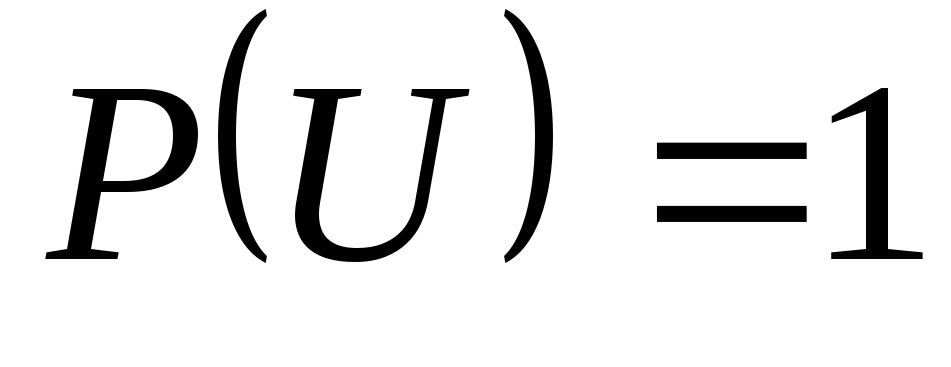3. Для неможливої події : .

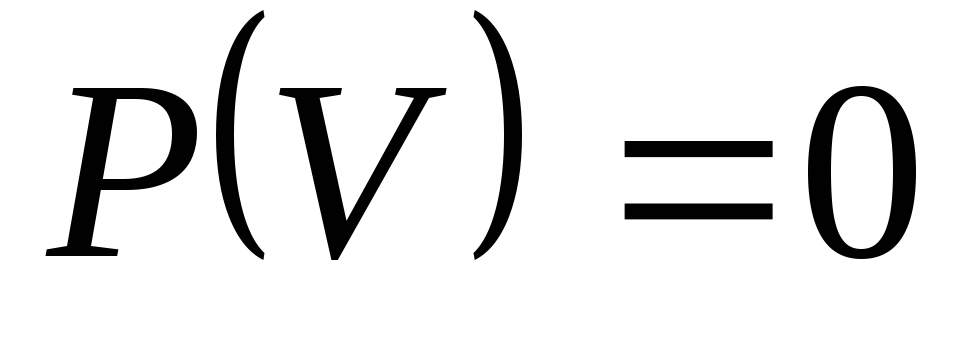Теорема (добутку імовірностей). Імовірність добутку двох подій і дорівнює добутку імовірності однієї з них на умовну імовірність іншої, при умові, що настала перша подія:

Доведення. Нехай - кількість подій (елементарних наслідків) у просторі елементарних подій, з яких подій сприяють появі , - сприяють появі , а - сприяють появі

За класичним означенням імовірності:

.

Аналогічно доводиться, що .

Теорема легко розповсюджується на випадок фіксованої кількості співмножників-подій. Наприклад, для трьох подій:

.

Наслідок 1 (формули визначення умовних імовірностей). Якщо імовірності подій відмінні від нуля, то

Зауважимо, що теорема добутку справедлива навіть у випадку нульових імовірностей подій.

Наслідок 2. Якщо подія не залежить від події , то і навпаки, подія не залежить від події , тобто вони взаємно незалежні.

Доведення.

Наслідок 3. Із незалежності подій і випливає незалежність пар подій : і , і , і .

Наслідок 4. Імовірність добутку двох незалежних подій дорівнює добутку їх імовірностей:

.

Наслідок легко розповсюджується на випадок фіксованої кількості співмножників-подій.

2. Теорема. Імовірність суми двох подій і дорівнює сумі імовірностей цих подій без імовірності їх добутку. Іншими словами, імовірність появи хоча б однієї із двох подій дорівнює сумі їх імовірностей без імовірності їх сумісної появи:

Доведення. Для доведення скористуємось діаграмою теореми добутку (див.вище). За класичним означенням :

Зауважимо, що теорема досить важко розповсюджується на випадок скінченної кількості доданків-подій. Так, наприклад, для трьох подій:

Наслідок 1. Імовірність суми двох несумісних подій дорівнює сумі їх імовірностей:

.

Наслідок легко розповсюджується на випадок фіксованої кількості несумісних подій-доданків.

Наслідок 2. Сума імовірностей подій , що утворюють повну групу, дорівнює одиниці:

.

Наслідок 3. Для взаємно протилежних подій і :

Наслідок 4 . Імовірність появи хоча б однієї із подій дорівнює:

.

Зокрема, якщо події незалежні в сукупності, то:

3.Теорема. Нехай подія може настати лише сумісно з хоча б однією із подій-гіпотез , які утворюють повну групу. Тоді імовірність (повна імовірність) події дорівнює:

тобто сумі добутків імовірностей гіпотез на умовні ймовірності події, при умові, що настала відповідна гіпотеза.

Доведення. За умовою А=А(Н₁+Н₂+…+Н_n)=A*H₁+A*H₂+…+A*H_n

P(A)=P(H₁*A+H₂*A+…+H_n*A)= [за теоремою суми] = P(H₁*A)+P(H₂*A)+…+P(H_n*A) = [за теоремою добутку] = P(H₁)*P_H1(A)+…+P(H_n)*P_Hn(A)

4.Формули Байєса.

Теорема. Нехай подія може настати лише сумісно з хоча б однією із подій-гіпотез , які утворюють повну групу. Якщо подія настала, то умовні (уточнені) імовірності гіпотез дорівнюють:

де повна імовірність

Доведення. Зазначимо, що виконуються усі умови теореми – формули повної ймовірності. Розглянемо одну із подій і скористуємось теоремою добутку:

Звідси:

де - повна імовірність.

Зауваження. Доведені формули називають формулами переоцінки гіпотез. В них приймають участь апріорні (до випробування) імовірності гіпотез та їх апостеріорні (після випробування) ймовірності , тобто формули дають можливість переоцінити ймовірності гіпотез після настання події.

8. У багатьох практичних задачах немає необхідності мати закон розподілу ВВ, а достатньо знати лише деякі її числові характеристики: математичне сподівання, дисперсію, середнє квадратичне відхилення, початкові та центральні моменти.

Означення. Математичним сподіванням (середнім значенням або центром розподілу) ДВВ називається сума добутків всіх її значень на відповідні ймовірності, тобто

Зауваження. Для будь-якої ДВВ із скінченною множиною значень математичне сподівання існує (і є невипадковим, сталим числом) і має таку саму розмірність, що й сама ДВВ. У випадку нескінченної зліченої множини значень ДВВ її математичне сподівання (МС) визначається як сума ряда, який може розбігатись, і тому МС може не існувати.

Означення. Дисперсією ДВВ називається МС квадрата відхилення ВВ від свого МС, тобто:

Дисперсія (якщо вона існує) має розмірність квадрата ВВ, є невипадковою сталою невід’ємною величиною, що характеризує розсіювання значень ВВ від центру розподілу – МС.

Для того, щоб мати аналогічну характеристику такої ж розмірності як сама ВВ, розглядають середнє квадратичне відхилення (стандарт): .