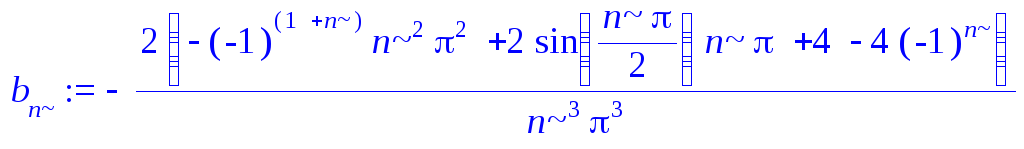5.4. Построение графиков частичных сумм степенного ряда

Разложение функций в ряд Тейлора или в ряд Маклорена является одной из важных задач в курсе высшей математики. При этом частичные суммы таких рядов аппроксимируют функцию в окрестности точки. Различие между ними при удалении от центра разложения можно определить визуально, построив график самой функции и графика частичных сумм.

Пример 5.6.Найти несколько членов разложения в ряд Маклорена функциии построить графики функции и частичных сумм.

Решение.Решение задачи проведем в программе Maple

Классическое окно	Стандартное окно
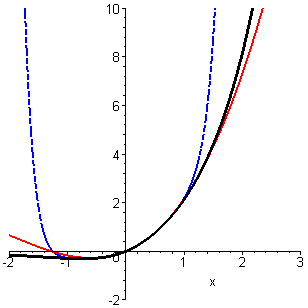
> f:=x->exp(x)*arctan(x); > S[3]:=convert(series(f(x),x=0,4),polynom); > S[10]:=convert(series(f(x),x=0,11),polynom); > plot([f(x),S[3],S[10]],x=-2..3,view=[-2..3,-2..10], color=[black,red,blue],thickness=[3,2,2], linestyle=[solid,dash,dash]);

Рисунок 5.7 – График функции и частичных сумм

Из графиков видно, что частичные суммы хорошо аппроксимируют функцию на отрезке [-1; 1], а дальше уже существенно отличаются.

5.5. Построение графиков периодических функций и графиков частичных сумм ряда Фурье

Построение графиков периодических функций, которые выражаются через периодические тригонометрические функции, выполняется стандартными методами построения графиков. Другое дело если периодическая функция представляет собой периодическое распространение на всю числовую ось произвольного выражения, заданного на каком-то промежутке. В этом случае построение графиков таких периодических функций сводится к заданию функции на этом промежутке и дальнейшего распространения графика данной функции на этом промежутке на всю числовую ось. В результате получается последовательность одинаковых графиков, смещенных на период.

Пример 5.7.Построить график периодической функции, заданной условиями

Решение.Сначала зададим функцию на промежутке [- 2; 2) с помощью функции piecewise , которая определяет кусочно заданные функции

Классическое окно	Стандартное окно
> f:=x->piecewise(x<-2,0,x<-1,2,x<0,-2*x,x<2,x^2,0);
Далее задаем значение периода и определяем необходимое для отображения число периодических построений в виде последовательности графиков P[k].
> T:=4: for k from -3 to 3 do P[k]:=plot(f(x+T*k), x=-2-T*k..2-T*k,discont=true,thickness=2): od:
Отображаем графики в одном окне (рисунок 5.8)
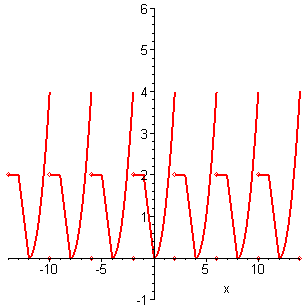
> display(seq(P[k],k=-3..3),view=[-14..14,-1..6]);

Рисунок 5.8 – График периодической функции

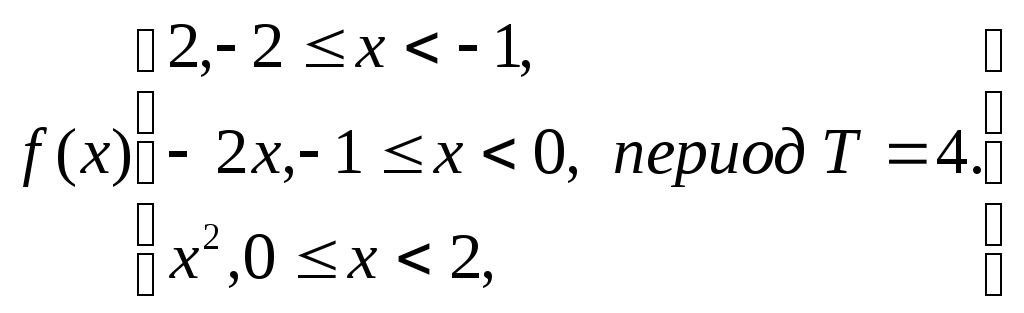
Периодические функции раскладываются в ряд Фурье по тригонометрической системе функций. Ряд Фурье для функций с периодом T=2l имеет вид

,

где коэффициенты ряда Фурье рассчитываются по формулам

.

Пример 5.8. Найти коэффициенты ряда Фурье периодической функции из предыдущего примера и построить в одном окне график функции и частичной суммыполученного ряда Фурье.

Решение.Используя задание функции в предыдущем примере, найдем коэффициенты ряда Фурье по записанным выше формулам.

Классическое окно	Стандартное окно
> assume(n,integer): > a[0]:=1/2*int(f(x),x=-2..2); > a[n]:=simplify(1/2*int(f(x)*cos(n*Pi*x/2),x=-2..2)); > b[n]:=simplify(1/2*int(f(x)*sin(n*Pi*x/2),x=-2..2));

Определяем графический объект P0 в виде последовательности графиков периодической функции, определенных в предыдущем пункте

Классическое окно	Стандартное окно
> P0:=seq(P[k],k=-3..3):
Находим частичную сумму и строим график периодической функции и этой частичной суммы (рис.5.9)
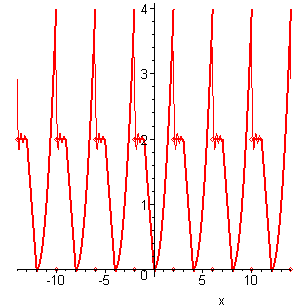
> S[10]:=a[0]/2+sum(a[n]*cos(n*Pi*x/2)+b[n]*sin(n*Pi*x/2), n=1..10): P1:=plot(S[10],x=-14..14): display(P0,P1);

Рисунок 5.9 – График периодической функции и частичной суммы

Из графика видно, что частичная сумма хорошо аппроксимирует периодическую функцию вдали от точек разрыва. Для точек, близких к точкам разрыва, необходимо брать частичные суммы с большим числом слагаемых.