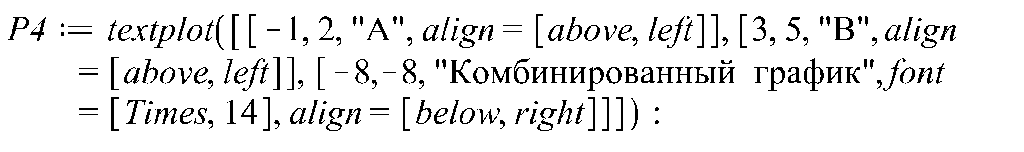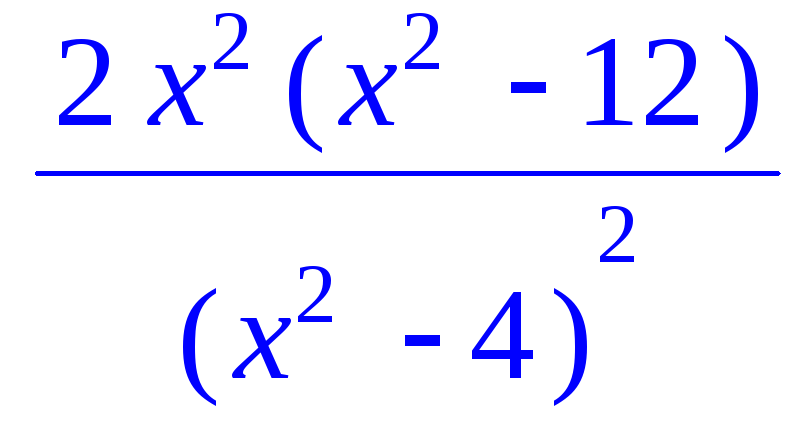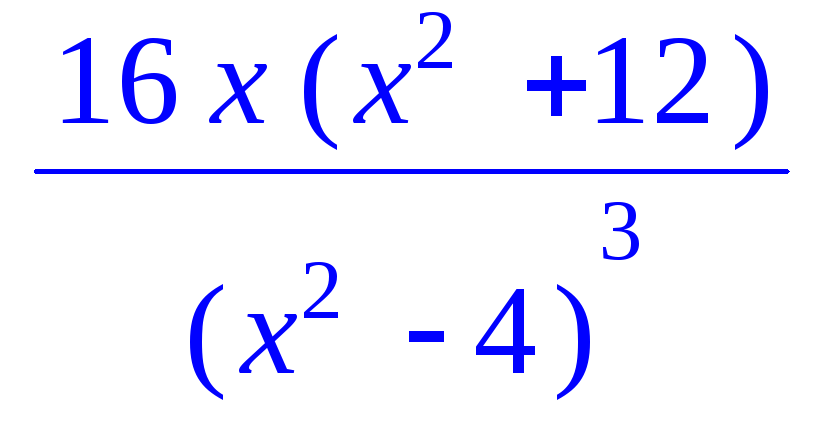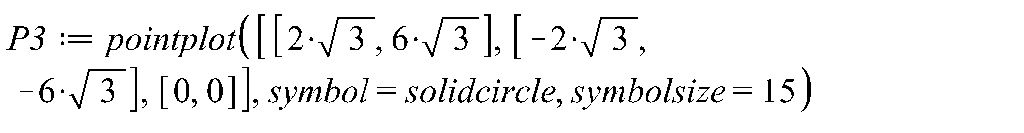4.3. Комбинированные графики
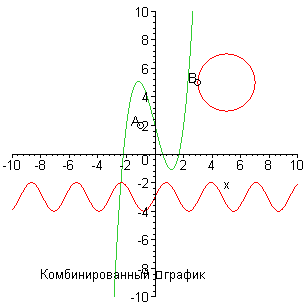
Часто на одном графике нужно отобразить несколько кривых, точек, текстовых фрагментов. Для этого сначала нужно создать отдельно каждый график со всеми характерными опциями, присваивая ему имя, то есть создать графический объект. Затем все созданные графические объекты отображаем на одном графике с помощью команды display пакета plots.
Пример 4.3.Построить в одном окне:
1) графики функций
и
;
2) график окружности
;
3) изображение точек A(-1,2) , B(4,5) . Поместить
внизу текст «Комбинированный график».
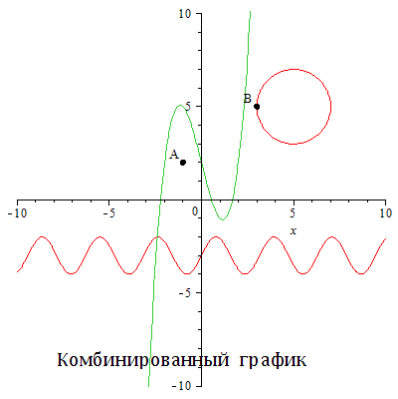
Решение.Создадим четыре графических объекта и поместим их на один график (рисунок 4.3)
|
Классическое окно |
Стандартное окно |
|
> P1:=plot([sin(2*x)-3,x^3-4*x+2],x=-10..10): P2:=implicitplot((x-5)^2+(y-5)^2=4,x=-10..10, y=-10..10, numpoints=10000): P3:=pointplot([[-1,2],[3,5]],style=point, symbol=solidcircle, symbolsize=15): P4:=textplot([[-1,2,"A",align=[above,left]], [3,5,"B", align=[above,left]],[-8,-8,"Комбинированный график", align=[below,right]]]): display(P1,P2,P3,P4,view=[-10..10,-10..10]);
|
>
>
>
>
>
>
|
Рисунок 4.3 – Комбинированный график
5. Графические построения при решении задач дисциплины «Математика»
При изучении дисциплины «Математика» имеется ряд задач прямо или косвенно связанных с построением графиков функций и других геометрических объектов. Например, при изучении раздела «Функции одной переменной» стандартной задачей является задача на исследование свойств функций и построение их графиков, в задачах на приложения интегралов требуется строить области интегрирования на плоскости или в пространстве. Данные задачи можно решать в Maple, сочетая вычислительные и графические возможности программы.
5.1. Исследование функций и построение их графиков
План исследования функций и построения их графиков включает в себя следующие основные пункты
1. Найти область определения функции и определить ее поведение на границах области определения; найти горизонтальные и вертикальные асимптоты.
2. Найти наклонные асимптоты.
3. Найти интервалы возрастания и убывания функции, экстремумы и вычислить значения функции в точках экстремума.
4. Найти интервалы выпуклости и вогнутости графика, точки перегиба и вычислить значения функции в точках перегиба.
5. Построить график функции.
Пример 5.1.Провести полное исследование
функции
и построить ее график.
Решение.Будем решать данный пример в программе Maple.
|
Классическое окно |
Стандартное окно |
|
1) Определим функцию в программе с помощью оператора f:=x->f(x), где f(x) некоторое выражение от переменной | |
|
> f:=x->2*x^3/(x^2-4);
|
>
|
|
Найдем точки разрыва функции с помощью функции discont(f(x),x) | |
|
> discont(f(x),x);
|
>
|
|
Таким образом,
область определения функции есть
объединение трех промежутков
| |
|
> Limit(f(x),x=-infinity)=limit(f(x),x=-infinity);
> Limit(f(x),x=-2,left)=limit(f(x),x=-2,left);
> Limit(f(x),x=-2,right)=limit(f(x),x=-2,right);
> Limit(f(x),x=2,left)=limit(f(x),x=2,left);
> Limit(f(x),x=2,right)=limit(f(x),x=2,right);
> Limit(f(x),x=infinity)=limit(f(x),x=infinity);
|
>
>
>
>
>
|
.
Исследуем поведение функции на
границах области определения с
помощью функции limit(f(x),x=a).
Следовательно,
– если
,
– если
,
– если
,
– если
2
x слева, то y -¥,
– если
2
и,
– если
.
Поэтому горизонтальных асимптот нет, вертикальные асимптоты:
x = -2 и x = 2.
2) Проверим существование наклонных асимптот y=kx+b по формулам
|
Классическое окно |
Стандартное окно |
|
> k:=limit(f(x)/x,x=-infinity); b:=limit(f(x)-k*x, x=-infinity);
|
>
|
|
– y= 2x – наклонная
асимптота при | |
|
> k:=limit(f(x)/x,x=infinity); b:=limit(f(x)-k*x, x=infinity);
|
>
|
|
– y=2x – наклонная
асимптота при
| |
.
.
3) Найдем первую производную
|
Классическое окно |
Стандартное окно |
|
> f1:=x->diff(f(x),x); normal(f1(x));
|
>
|
|
Приравнивая производную к нулю, найдем ее корни | |
|
> z:=[solve(f1(x)=0,x)];
|
>
|
Всего получилось три корня, из которых корень x =0 имеет кратность 2.
Корни записаны в индексированный
список z[i],i= 1,2,3,4, так чтоz[1]=z[2]= 0,z[3]=
,z[4]=
.
Определим изменения знака производной
при переходе через корни:
|
Классическое окно |
Стандартное окно |
|
а) корень x =0 | |
|
> subs(x=z[1]-0.1,f1(x)); subs(x=z[1]+0.1,f1(x));
|
>
|
|
Знак производной не меняется, поэтому x = 0 не является точкой экстремума. б) корень x= | |
|
> evalf(subs(x=z[4]-0.1,f1(x))); evalf(subs(x=z[4]+0.1,f1(x)));
|
>
|
|
Знак производной
меняется с + на -, поэтому точка x= | |
|
> f(z[4]); evalf(%);
|
>
|
|
в) корень x =
| |
|
> evalf(subs(x=z[3]-0.1,f1(x))); evalf(subs(x=z[3]+0.1,f1(x)));
|
>
|
|
Знак производной
меняется с - на+, поэтому точка x =
| |
|
> f(z[3]); evalf(%);
|
|
|
Определим участки возрастания и убывания функции. | |
|
> solve(f1(x)>0,x);
|
>
|
|
– на интервалах ( | |
|
> solve(f1(x)<0,x);
|
>
|
|
– на интервалах ( | |
является точкой локального максимума.
Значение функции в этой точке равно
является точкой локального минимума.
Значение функции в этой точке равно
)
и (
) функция возрастает.
), (-2;2) и (
)
функция убывает.
4) Найдем вторую производную
|
Классическое окно |
Стандартное окно |
|
> f2:=x->diff(f(x),x,x);normal(f2(x));
|
>
|
|
Найдем корни второй производной | |
|
> u:=[solve(f2(x)=0,x,real)];
|
>
|
|
Получился всего один корень x =0 . Проверим изменение знака второй производной при переходе через этот корень. | |
|
> evalf(subs(x=u[1]-0.1,f2(x))); evalf(subs(x=u[1]+0.1,f2(x)));
|
>
|
|
Знак меняется, следовательно, точка x =0 является точкой перегиба. Значение функции в точке перегиба равно 0: | |
|
> f(0);
|
>
|
|
Определим участки выпуклости вниз (вогнутости) и выпуклости вверх (выпуклости) графика функции. | |
|
> solve(f2(x)>0,x);
|
>
|
|
на интервалах (-2;0)
и (2;+
| |
|
> solve(f2(x)<0,x);
|
>
|
|
– на интервалах
( | |
)
график функции является выпуклым
вниз (вогнутым).
;-2)
и ( 0; 2) график функции является выпуклым
вверх (выпуклым).
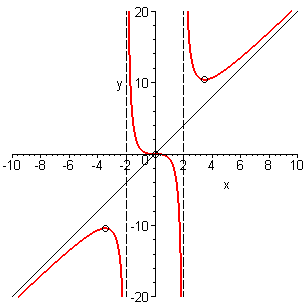
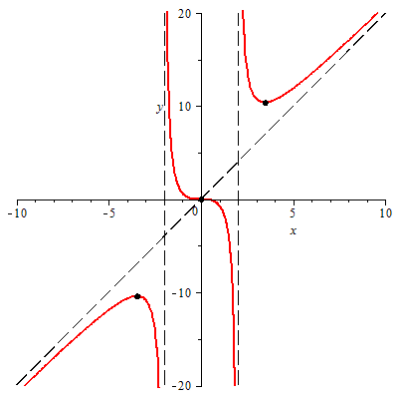
По данным исследования строим график функции. Представим его в виде графика самой функции, графиков асимптот и графиков точек экстремума (рисунок 5.1).
|
Классическое окно |
Стандартное окно |
|
> with(plots): > P1:=plot(f(x),x=-10..10,y=-20..20,discont=true, color=red,thickness=2): |
|
|
– график самой функции; | |
|
> P2:=implicitplot([x=-2,x=2,y=2*x],x=-10..10, y=-20..20,color=black,thickness=1,linestyle=dash): |
|
|
– графики асимптот; | |
|
> P3:=pointplot([[2*sqrt(3),6*sqrt(3)],[-2*sqrt(3), -6*sqrt(3)],[0,0]],symbol=solidcircle,symbolsize=15): |
|
|
– графики точек экстремума и точки перегиба | |
|
> display(P1,P2,P3);
|
|
Рисунок 5.1 – График функции
