
1 (1)
.docx11. дифференциалые уравнения высших порядков .начальные условия.
F
(x;
y;
y’;…;
y(n))
– дифференциальное уравнение n
– порядка или y(n)
= f(x;
y;
y’;
…; y(n-1))
Общим решением этого уравнения является:
y
= j(x;
c1;
c2;…;
cn)Для
дифференциального уравнения n
– порядка имеет место теорема Коши о
существовании и единственности частного
решения уравнения при данных n
– начальных условиях. Например для
дифференциального уравнения второго
порядка.
Теорема Коши: y``=f(x,y,y`)начальные
условия: x=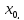 y(
y(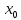 )=y0,
y`(x0)=y`0.
Если
f(x,y,y`)непрерывна
в точке (x0,y0,y`0)и
в этой точке непрерывна частная
производная f`y`,
то существует, причём единственное
частное решение, удовлетворяющее данным
начальным условиям .y*=
φ
(x,C*1,C*2)
)=y0,
y`(x0)=y`0.
Если
f(x,y,y`)непрерывна
в точке (x0,y0,y`0)и
в этой точке непрерывна частная
производная f`y`,
то существует, причём единственное
частное решение, удовлетворяющее данным
начальным условиям .y*=
φ
(x,C*1,C*2)
12.теорема существования и единствености решения дифференциалые уравнения высших порядков .
Теорема существования и единственности решения задачи Коши.
Задачей Коши для ДУ n -го порядка называется задача отыскания его частного решения у = у(х), которое удовлетворяет начальным условиям:y(x0)=y0;y`(x0)=y`0;y``(x0)=y``0;…;y(n-1)0(x0)=y(n-1), где x0, y`0.y``0….. y(n-10 заданные числаТаким образом, решение задачи Коши для ДУ n -го порядка сводится к нахождению интегральной кривой, проходящей через точку M0(x0, y0,y`0.y``0….. y(n-10 ) из области определения (D ) функции f(x,y,y`0,y``,..,y(n-1))
Теорема. Задача Коши для ДУ n -го порядка имеет единственное решение, если:
-
f(x,y,y`0,y``,..,y(n-1)) непрерывна в области D ;
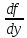 ,
,
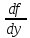 ,
,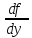 ,…,
,…,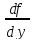 непрерывны в области
D
.
непрерывны в области
D
.
В этом случае решение ДУ n -го порядка проходит через заданную точку M0(x0, y0,y`0.y``0….. y(n-10 )
13. методы понижения порядка уравнения
1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.Рассмотрим уравнения вида F(x,y(k),y(k-1),…,y(n))=0 (1≤k≤n).С помощью замены y(k)=u(x), где u - новая неизвестная функция, уравнение приводится к уравнению (n-k) -го порядка:F(x,u,u`,…,u(n-k))=0
2. Уравнения, не содержащие явно независимой переменной. Рассмотрим уравнения вида F(y,y`,..,y(n))=0 С помощью замены y`=p,(где p=p(y) - новая искомая функция независимая переменная) порядок уравнения понижается на единицу, так как
Y``=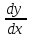 =
=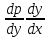 =pp`
=pp`
y```= =
=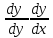 =(p``p+p`2)p
=(p``p+p`2)p
Данная подстановка дает уравнение (n-1) - го порядка относительно новой неизвестной функции p:F1(y,p,p`,..,p(n-1))=0 При осуществлении такой замены возможна потеря решения y=const. Непосредственной подстановкой необходимо проверить наличие у уравнения решений такого вида.
14. понятие первого интеграла. Задача каши. нормальные системы дифференциальных уравнений
Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям .Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при t=0, а решение отыскивается при t>0.От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.Основные вопросы, которые связаны с задачей Коши, таковы:
-
Существует ли (хотя бы локально) решение задачи Коши?
-
Если решение существует, то какова область его существования?
-
Является ли решение единственным?
-
Если решение единственно, то будет ли оно корректным, то есть непрерывным (в каком-либо смысле) относительно начальных данных?
Говорят, что задача Коши имеет единственное решение, если она имеет решение y=f(t)и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки (x0,y0)имеет поле направлений, совпадающее с полем направлений y=f(t). Точка (x0,y0)задаёт начальные условия.
15
Линейные однородные с частными. ур-ие
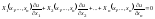 (
(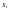 - данные функции аргументов
- данные функции аргументов
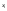 ,
определены в
,
определены в
 ,
,
 - искомая функция) – линейное однородное
с частными. Решением будет дифференцируемая
по
- искомая функция) – линейное однородное
с частными. Решением будет дифференцируемая
по
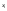 ,
которая при подстановке в исходное
превращает его в тождество. Геометрически
решение: поверхность в пр-ве переменных
x,
u
(интегральная п-ть). Систему обычных
диффуров, соответствующую ур-ию (1)
,
которая при подстановке в исходное
превращает его в тождество. Геометрически
решение: поверхность в пр-ве переменных
x,
u
(интегральная п-ть). Систему обычных
диффуров, соответствующую ур-ию (1)
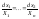 (2) - называют системой в симметричной
форме. (2) в силу условий, наложенных на
коэффициенты (1), можно записать в
нормальной форме
(2) - называют системой в симметричной
форме. (2) в силу условий, наложенных на
коэффициенты (1), можно записать в
нормальной форме
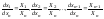 (3). Рассм. в области единственности общее
решение этой системы:
(3). Рассм. в области единственности общее
решение этой системы:
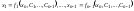 если удаётся разрешить эти ур-ия отн-но
если удаётся разрешить эти ур-ия отн-но
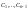 .
Получим
.
Получим
 (4) – каждое из этих ур-ий называется
первым интегралом системы (3), а каждая
из функций
(4) – каждое из этих ур-ий называется
первым интегралом системы (3), а каждая
из функций
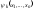 - интегралом этой же системы. Интегральные
кривые системы ур-ий (2) или (3) называют
х-ми ур-ия с частными производными (1).
Связь между решениями ур-ия (1) и интегралами
соответствующей системы обычных диффуров
(3) или (2): Т1.
Если
- интегралом этой же системы. Интегральные
кривые системы ур-ий (2) или (3) называют
х-ми ур-ия с частными производными (1).
Связь между решениями ур-ия (1) и интегралами
соответствующей системы обычных диффуров
(3) или (2): Т1.
Если
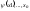 - интеграл системы (2) или (3), то
- интеграл системы (2) или (3), то
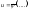 - решение (1). Т2.
Если
- решение (1). Т2.
Если
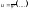 -
решение
(1),
то
-
решение
(1),
то
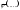 -
интеграл
(3).
Т3.
Общим решением (1), т.е. решением, которое
вмещает все без исключения решения
этого ур-ия, является
-
интеграл
(3).
Т3.
Общим решением (1), т.е. решением, которое
вмещает все без исключения решения
этого ур-ия, является
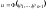 - произвольная дифференцируемая функция.
Задачей Коши для (1) наз-ся задача о
нахождении решения
- произвольная дифференцируемая функция.
Задачей Коши для (1) наз-ся задача о
нахождении решения
 ,
,
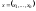 этого ур-ия, которое удовлетворяет
условию
этого ур-ия, которое удовлетворяет
условию
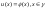 ,
где
,
где
 - гладкая гиперповерхность, а
- гладкая гиперповерхность, а
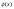 - начальное условие. Построение решения
(1) с нач. условием
- начальное условие. Построение решения
(1) с нач. условием
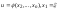 :
1.
находим базис первых интегралов
:
1.
находим базис первых интегралов
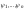 системы в симметричной форме (2),
соответствующей исходному (1). 2.
Составляем систему функциональных
ур-ий
системы в симметричной форме (2),
соответствующей исходному (1). 2.
Составляем систему функциональных
ур-ий
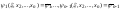 которую
разрешаем относительно
которую
разрешаем относительно
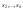 :
:
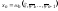 3.
строим функцию
3.
строим функцию
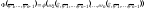 4.
Выписываем искомое решение по формуле
4.
Выписываем искомое решение по формуле
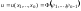 и если возможно проводим аналитическое
упрощение.
и если возможно проводим аналитическое
упрощение.
.
.
