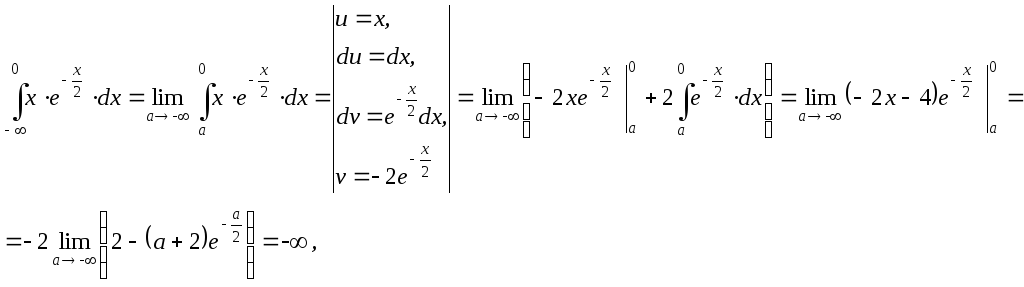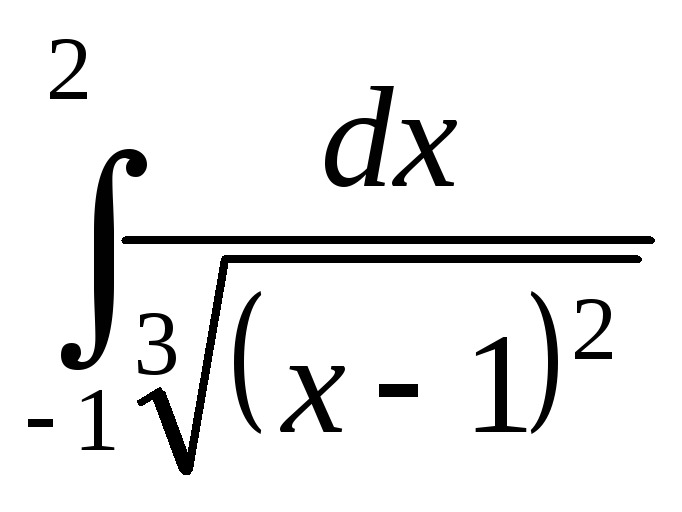- •Тема 1. Неопределенный интеграл
- •Задания для самостоятельного решения
- •Тема 2. Интегрирование рациональных функций
- •Задачи для самостоятельного решения
- •Тема 3. Интегрирование иррациональных функций
- •Задачи для самостоятельного решения
- •Тема 4. Интегрирование тригонометрических функций
- •Задачи для самостоятельного решения
- •Тема 5. Определенный интеграл
- •Задачи для самостоятельного решения
- •Тема 6. Несобственные интегралы
- •Задачи для самостоятельного решения
- •Тема 6. Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур
- •Задачи для самостоятельного решения
- •Тема 8. Приложения определенного интеграла. Вычисление длины дуги кривой
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
Используя формулу Ньютона-Лейбница вычислить интегралы:
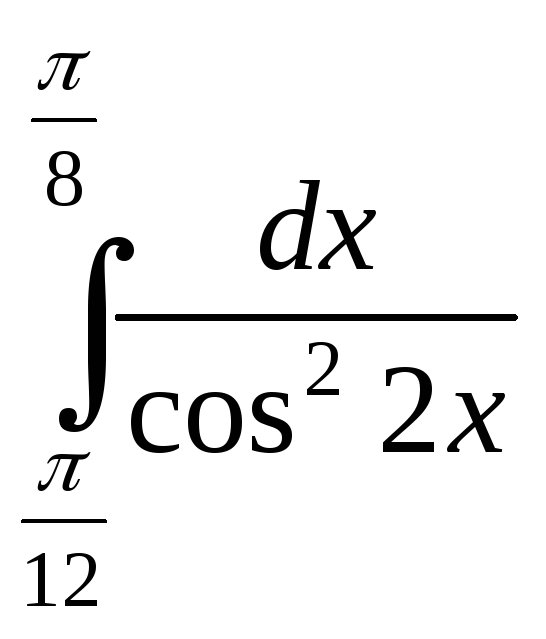 ;
;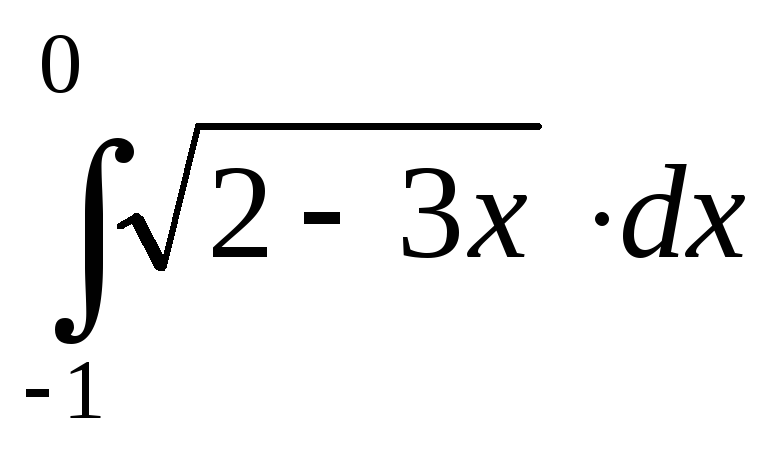 ;
;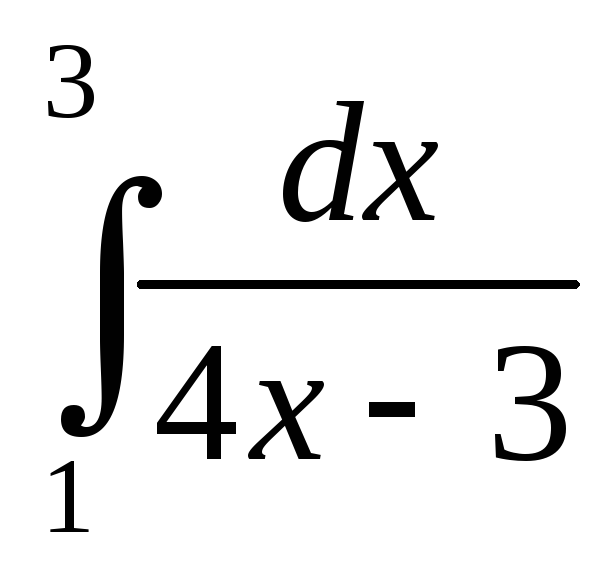 ;
;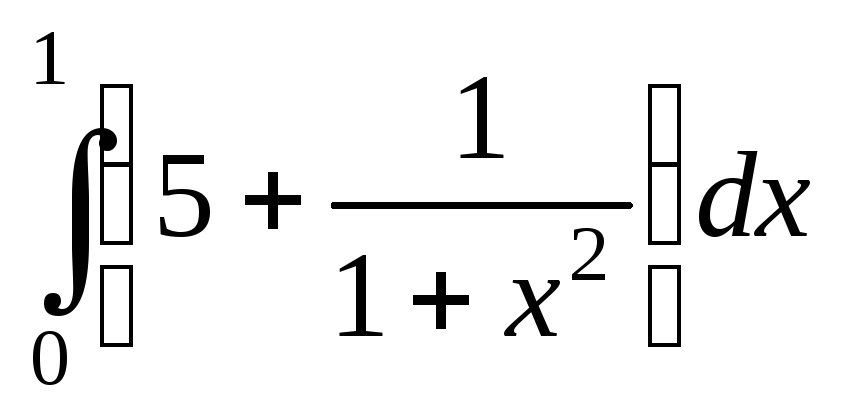 ;
;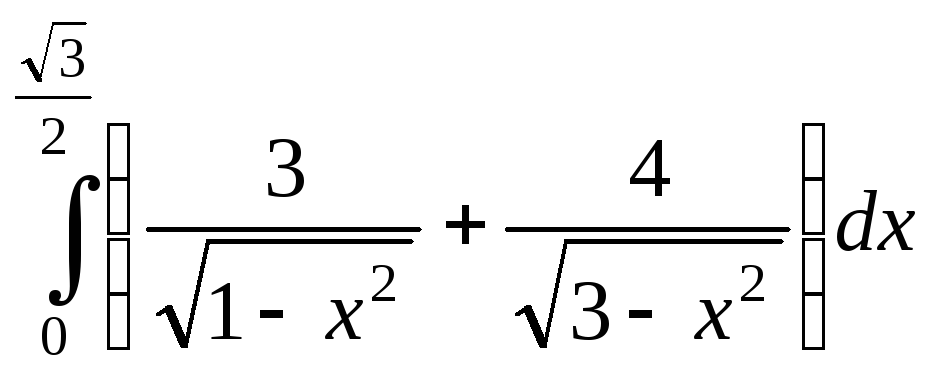
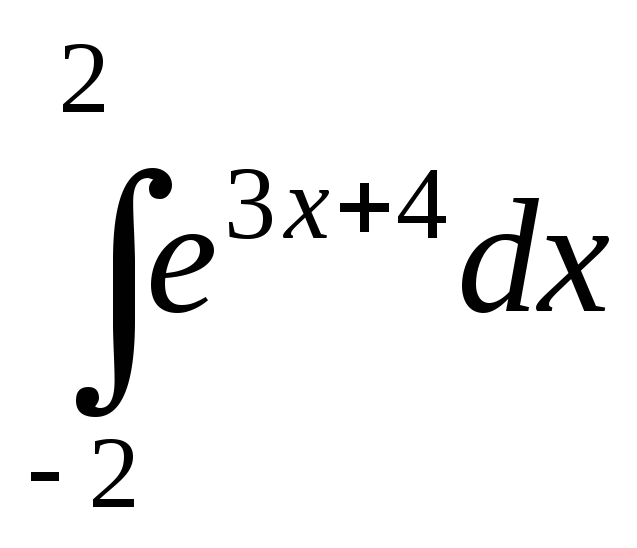 ;
;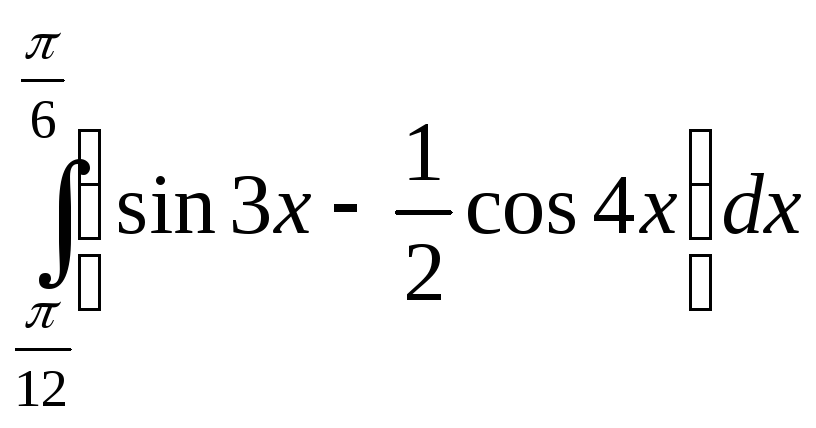 ;
;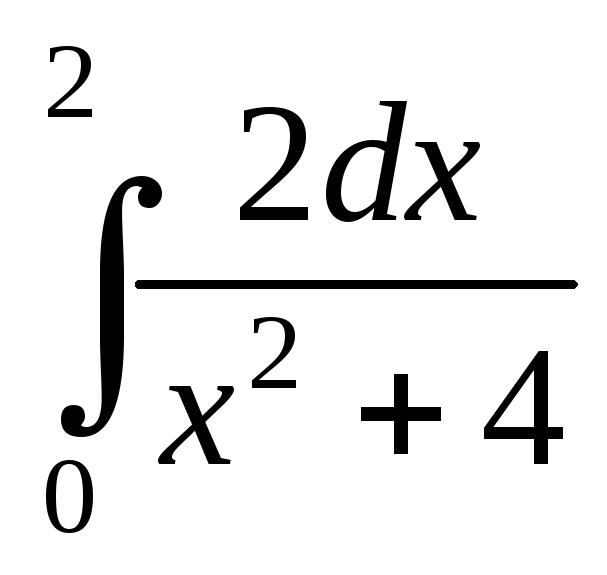 ;
;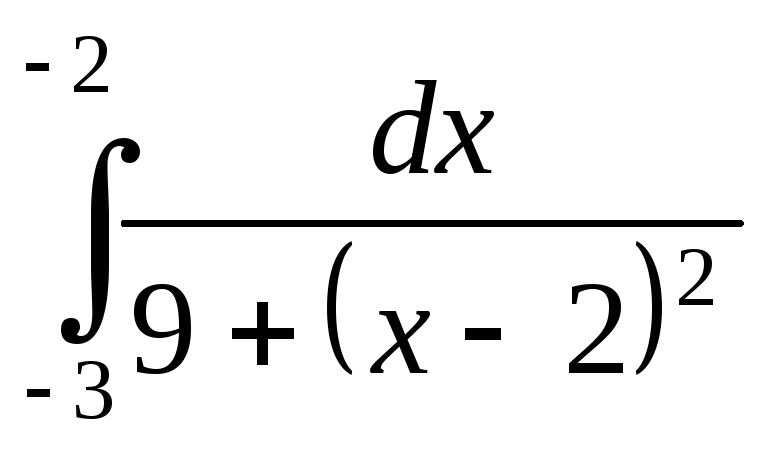 ;
; ;
;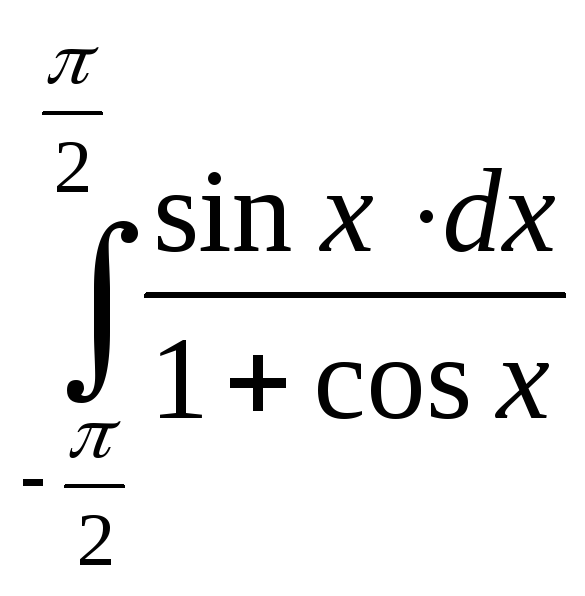 ;
;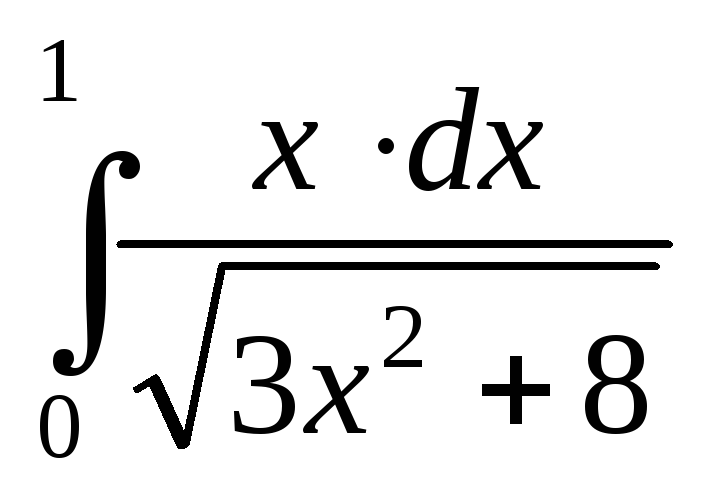 ;
;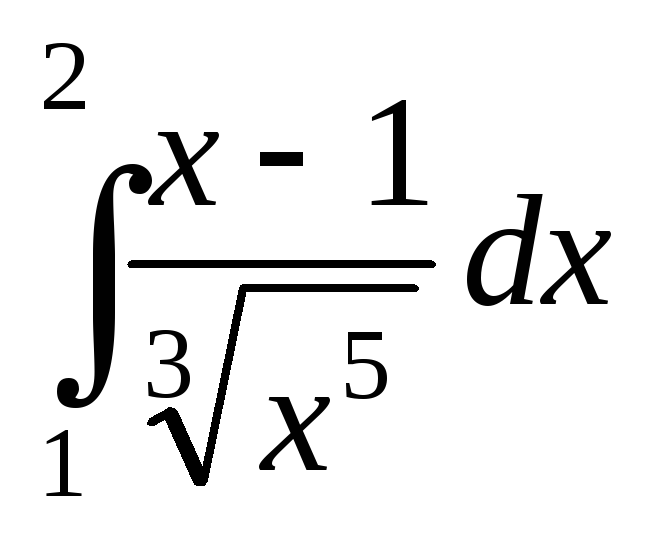 ;
;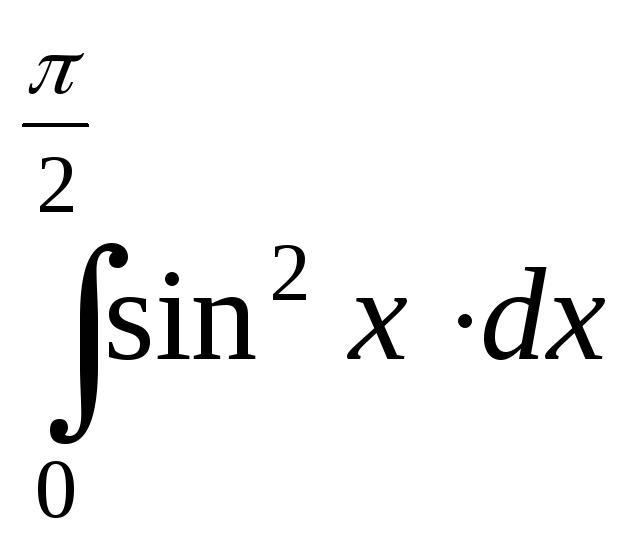 .
.
Вычислить определенные интегралы, используя подходящую замену переменных:
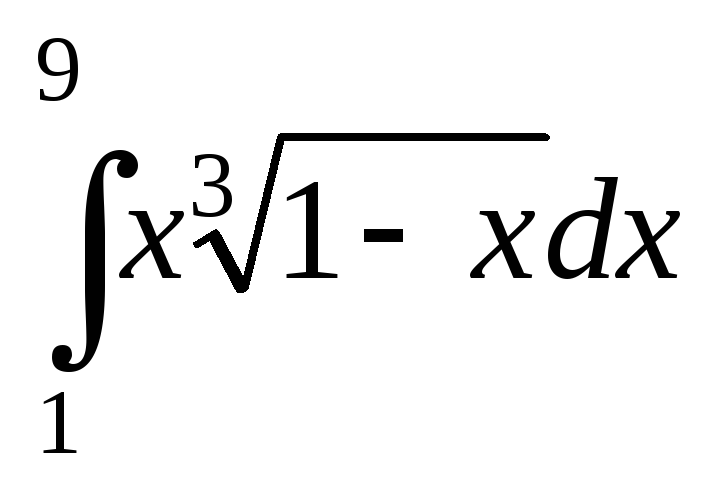 ;
;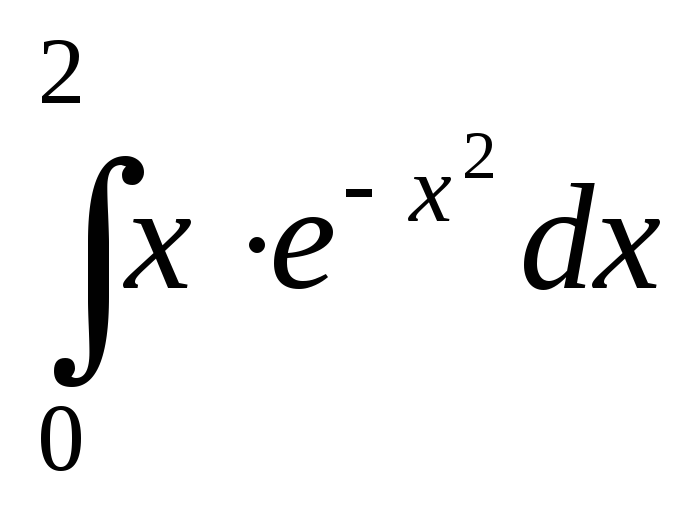 ;
; ;
;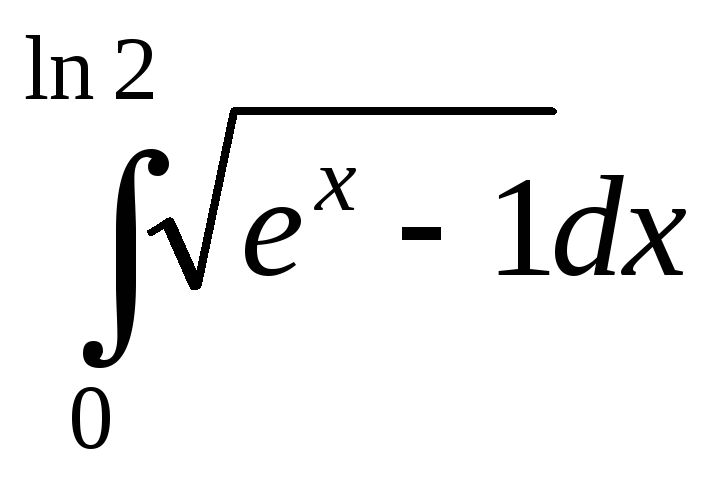 ;
;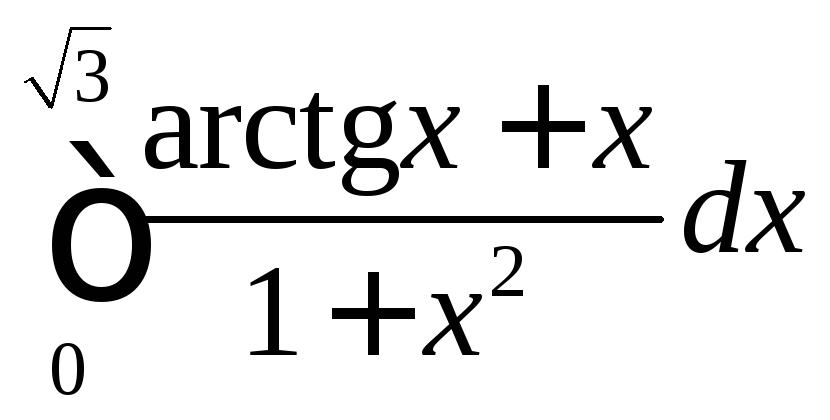 ;
;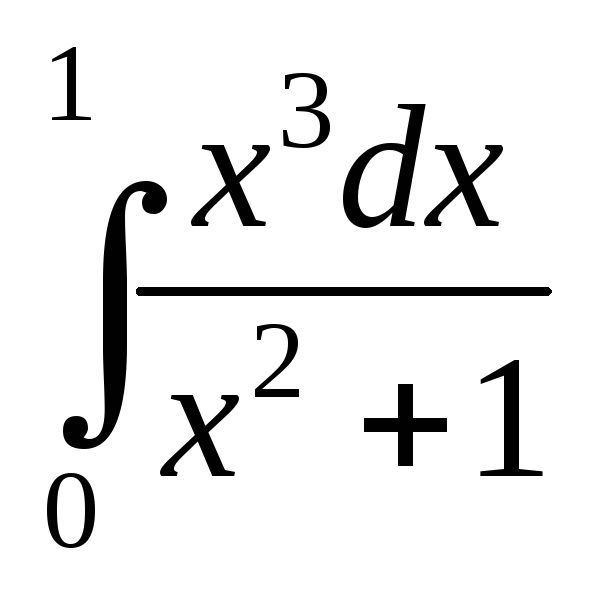 ;
;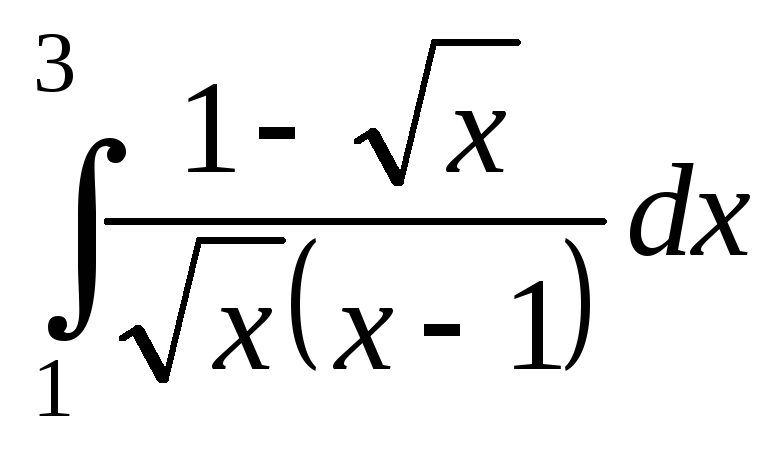 ;
;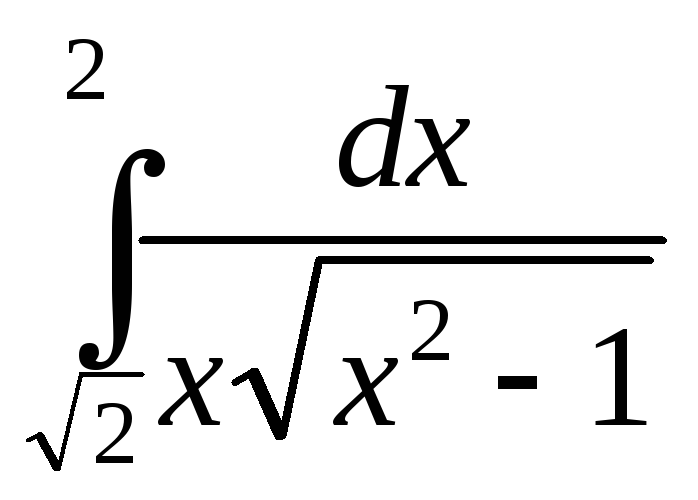 ;
;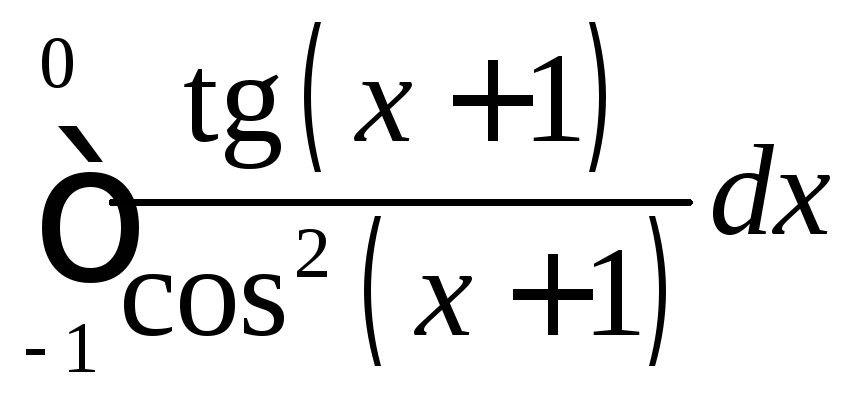 ;
;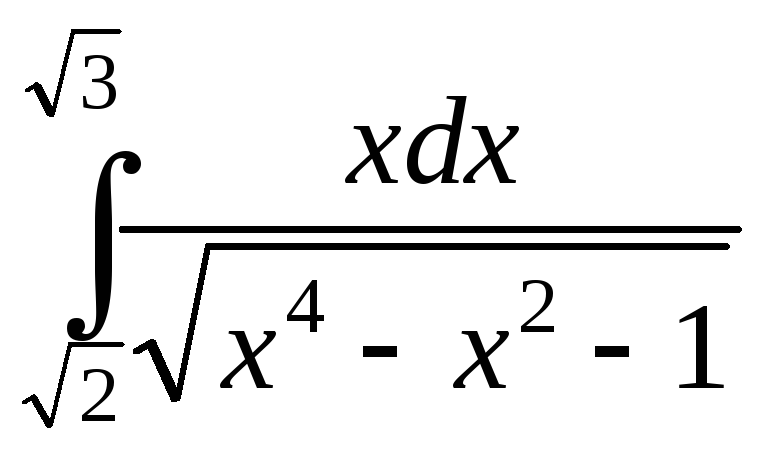
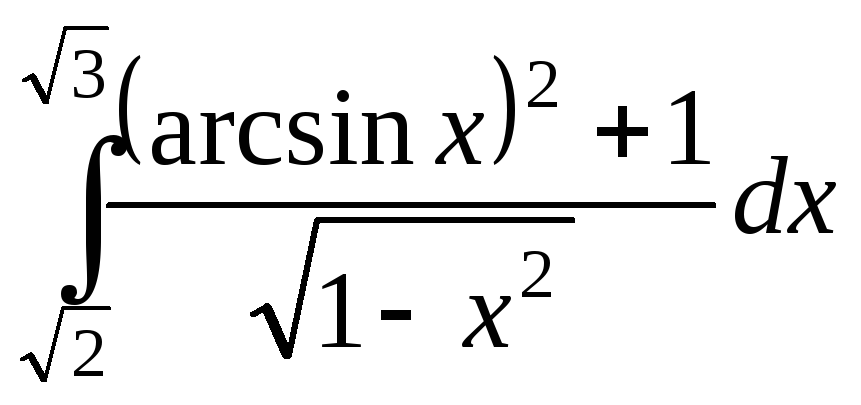 .
.
Используя формулу интегрирования по частям, найти интегралы:
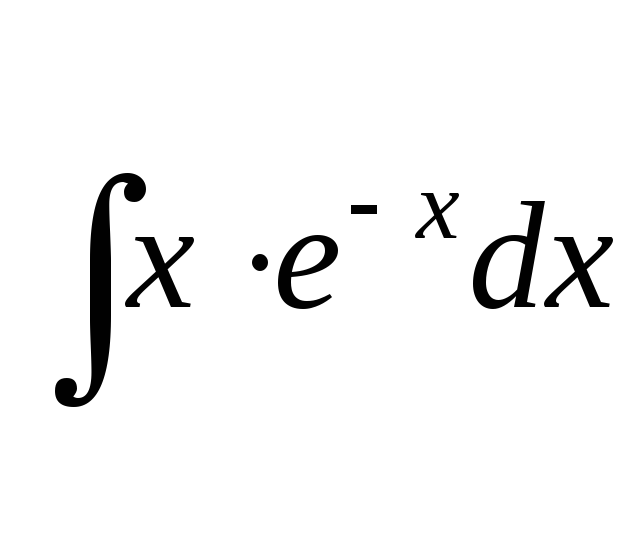 ;
;
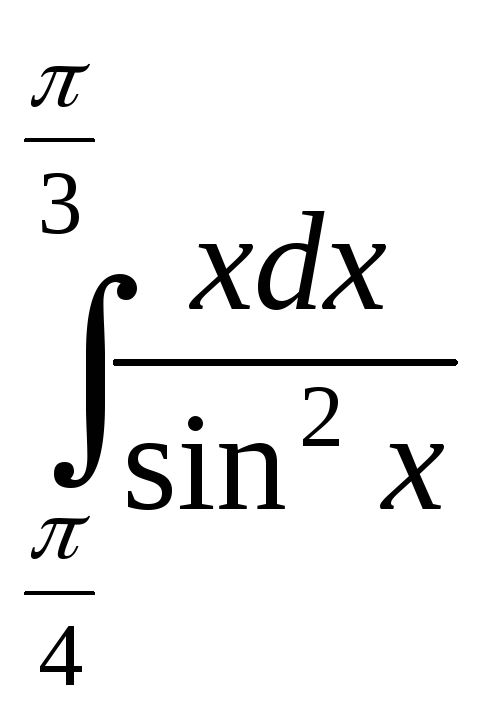 ;
;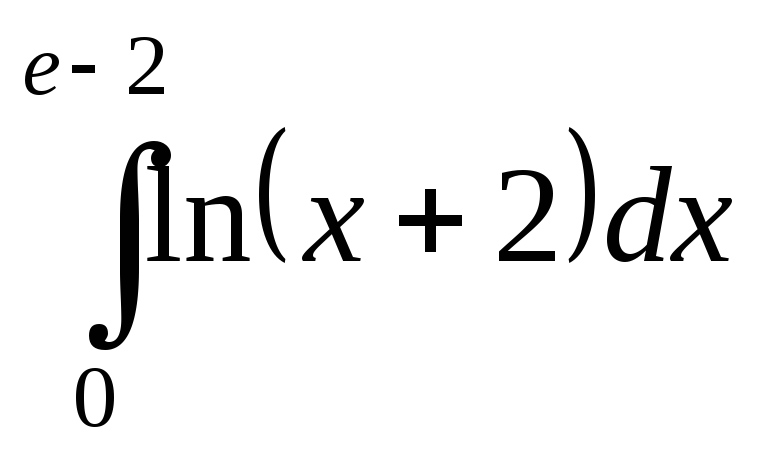 ;
;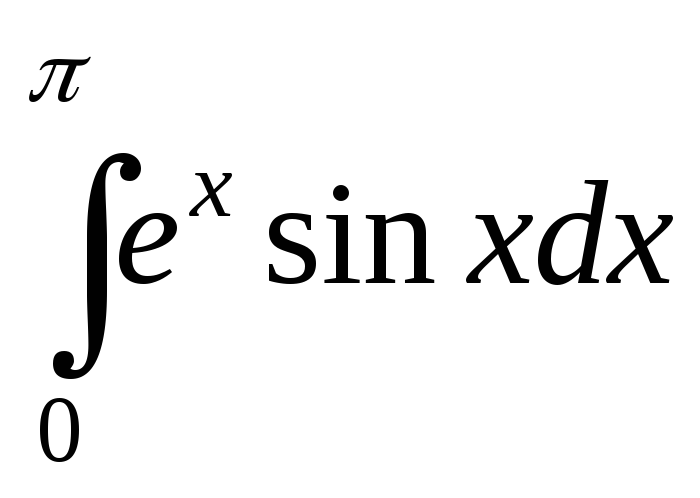 ;
;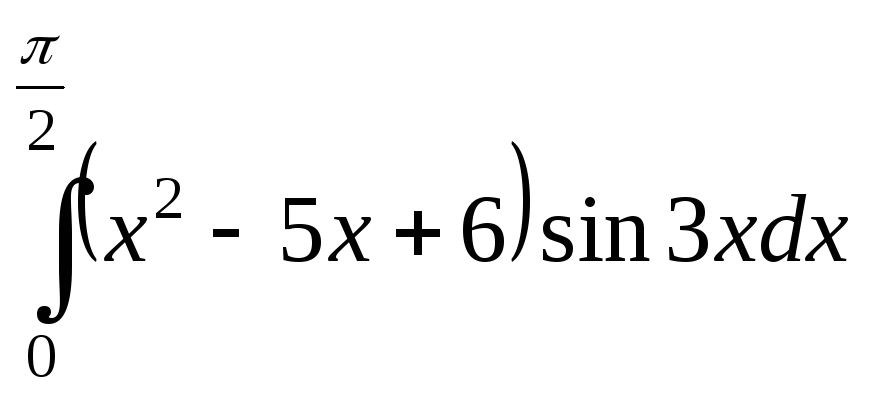 ;
;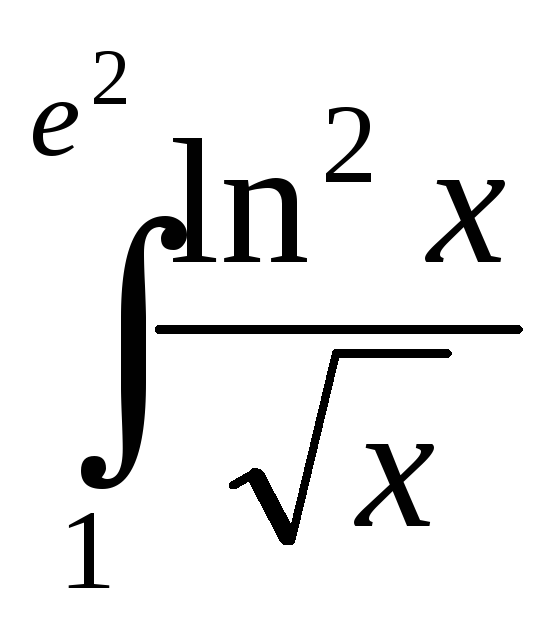 ;
;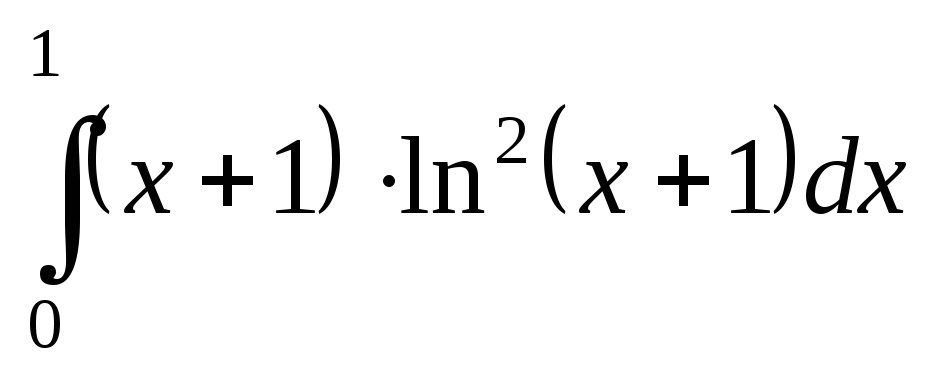 ;
; ;
;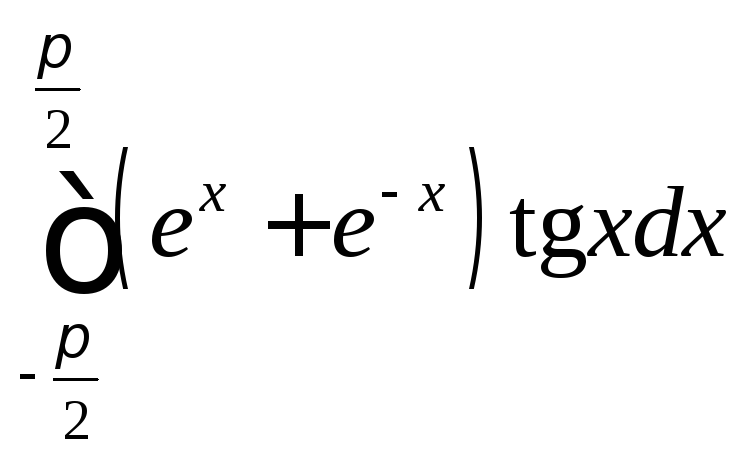 ;
;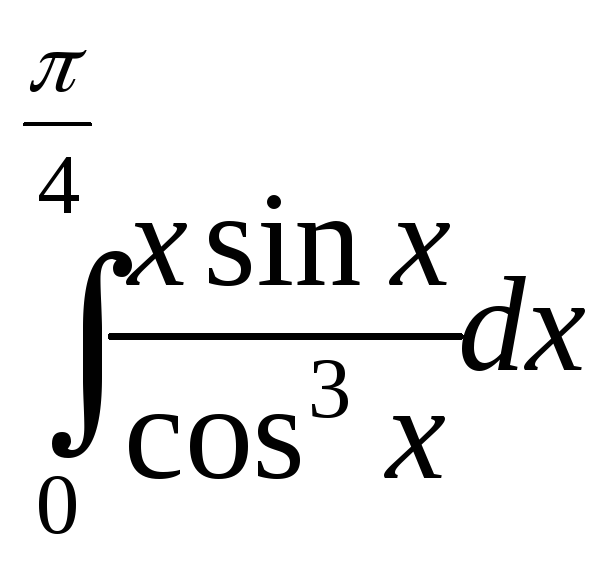 ;
;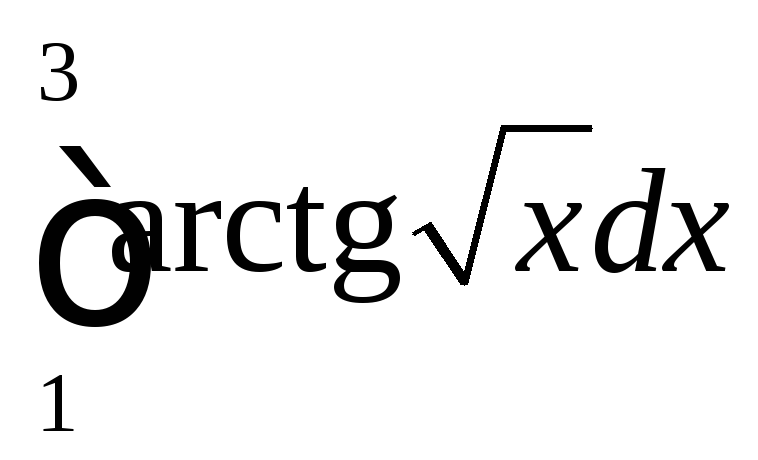 .
.
Тема 6. Несобственные интегралы
Вопросы для повторения:
Вычисление интегралов с бесконечными пределами (Iрода).
Вычисление интегралов от неограниченных функций (IIрода).
Пример 1. Вычислить несобственные интегралы или установить их расходимость:
По определению несобственного интеграла Iрода имеем:
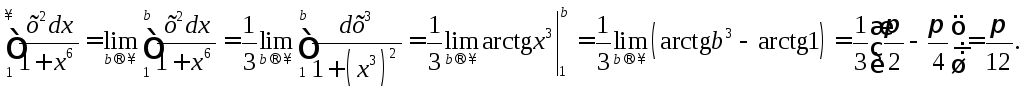
Интеграл сходится.
следовательно, интеграл расходится.
Разбиваем точкой х= 0 промежуток интегрирования на два интервала, а интеграл на два несобственных интеграла.
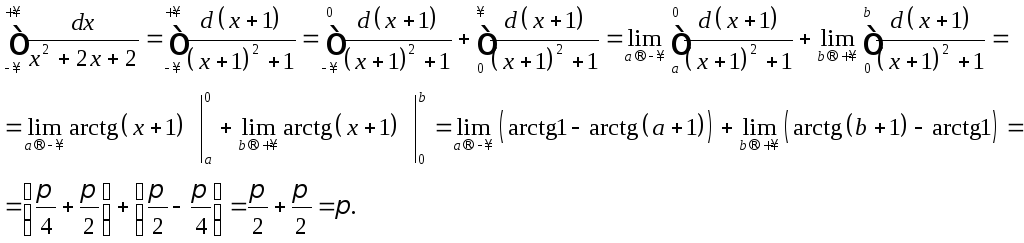
Интеграл сходится.
Пример 2. Вычислить несобственные интегралы или установить их расходимость:
Поскольку в точке х= 1, принадлежащей промежутку [-1, 2], функция терпит разрыв, то по определению несобственного интегралаIIрода получим:

Интеграл сходится.
Подынтегральная функция терпит разрыв в точке х= 1, т.е. на конце промежутке [1, 2]. Следовательно,
![]() Интеграл расходится.
Интеграл расходится.
Подынтегральная функция терпит разрыв при х= 2. Имеем:
![]()
Интеграл сходится.
Задачи для самостоятельного решения
I. Вычислить несобственные интегралы или установить их расходимость:
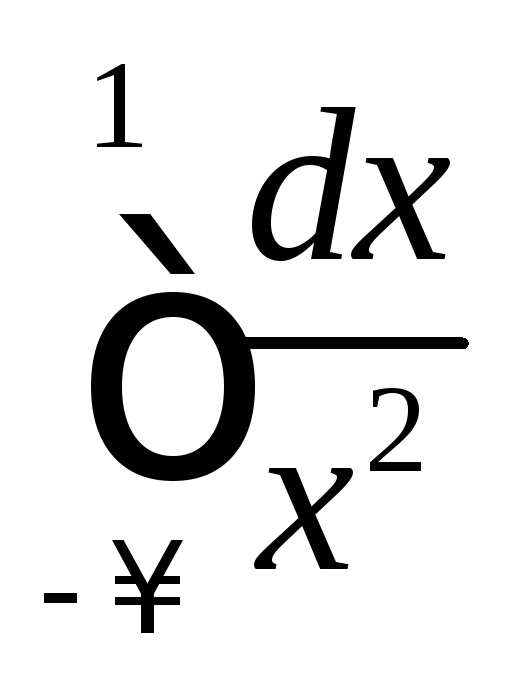 ;
;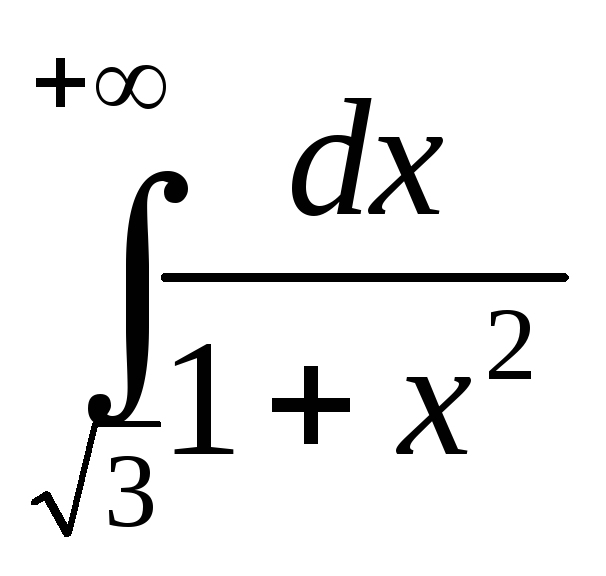 ;
;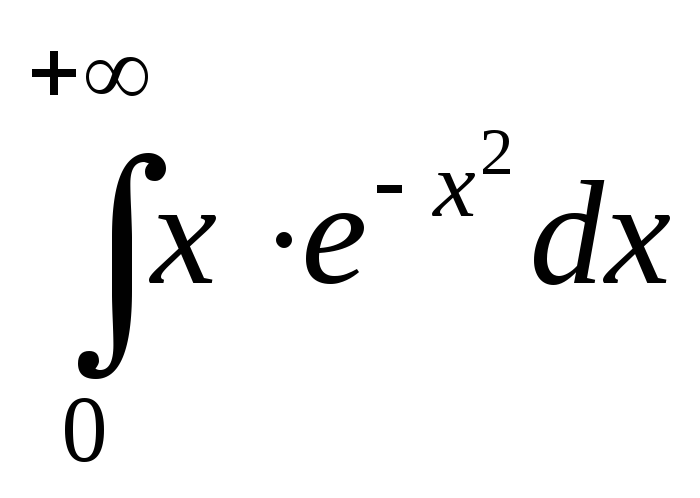 ;
;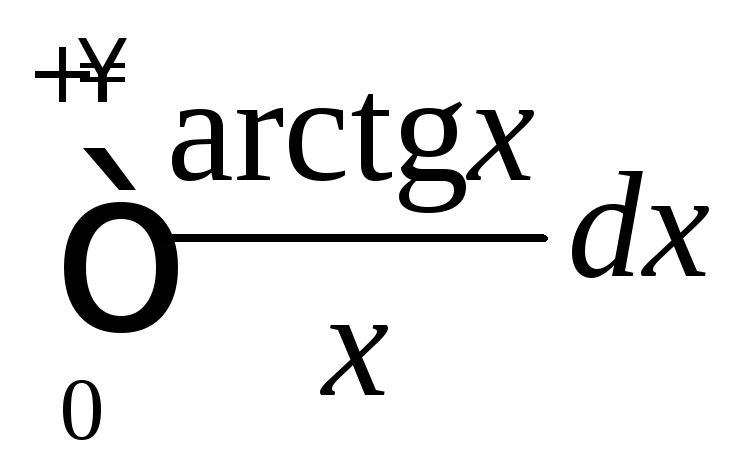 ;
;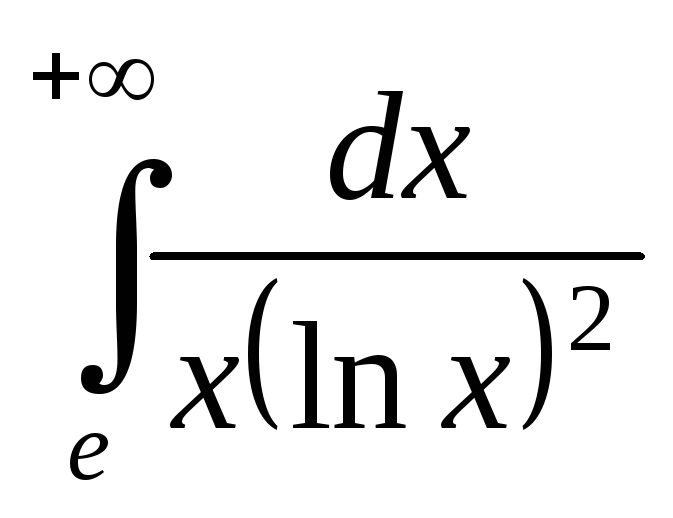 ;
;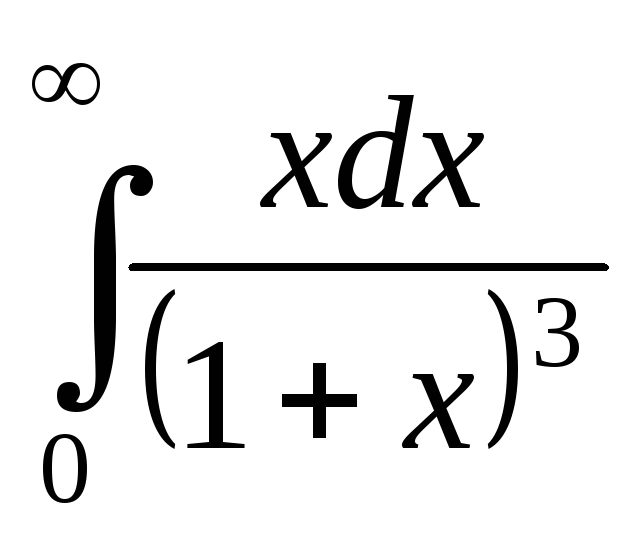 ;
;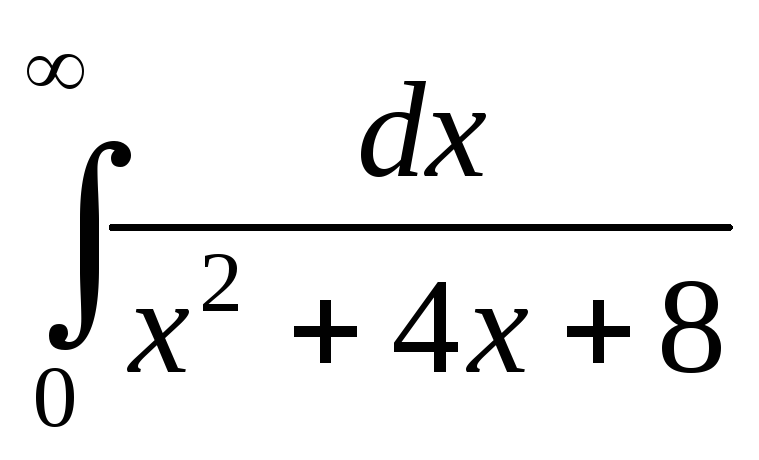 ;
;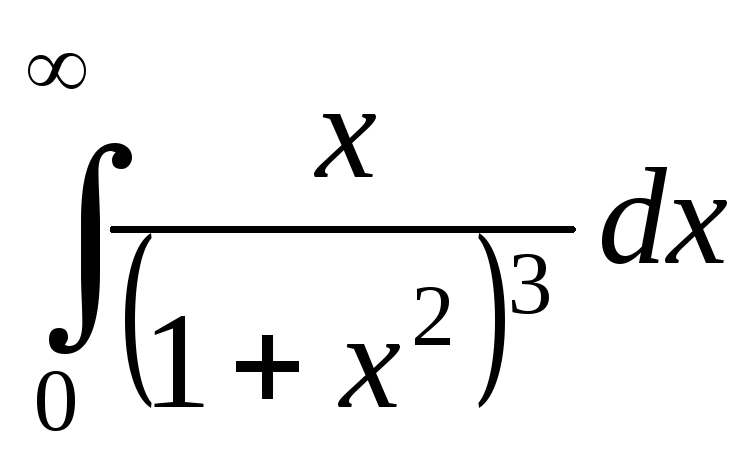 ;
;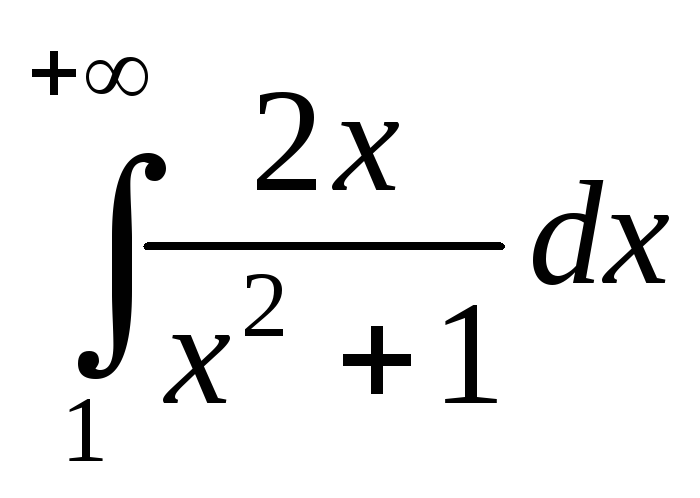 ;
;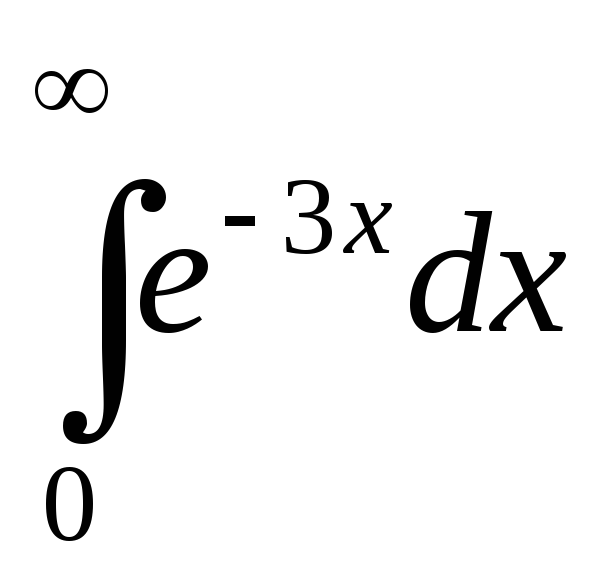 ;
;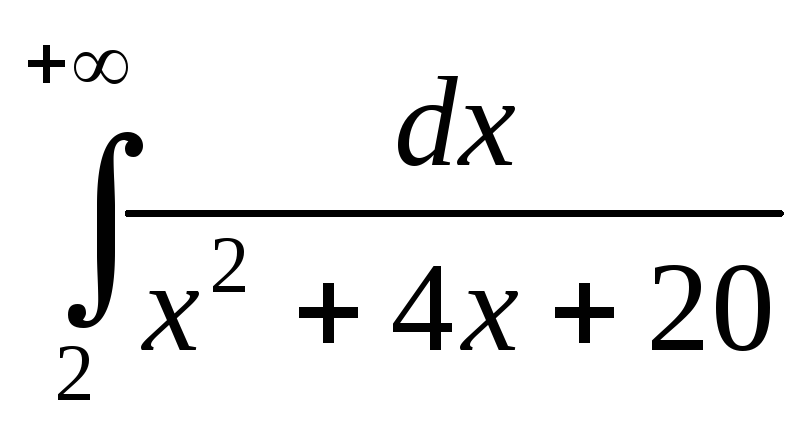 ;
;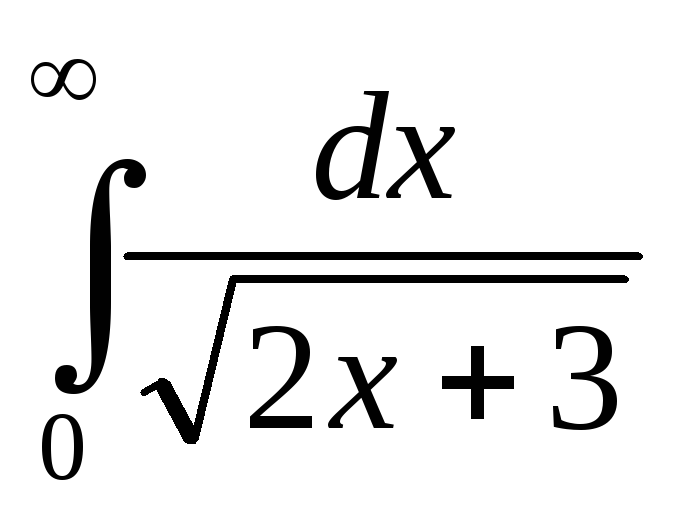 ;
;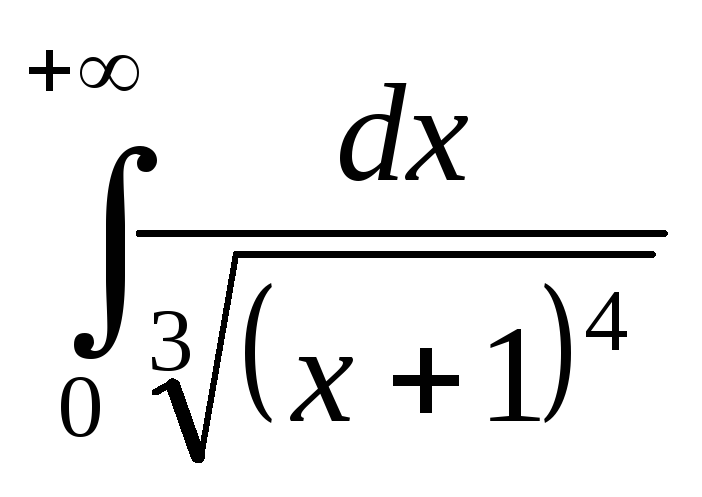 ;
;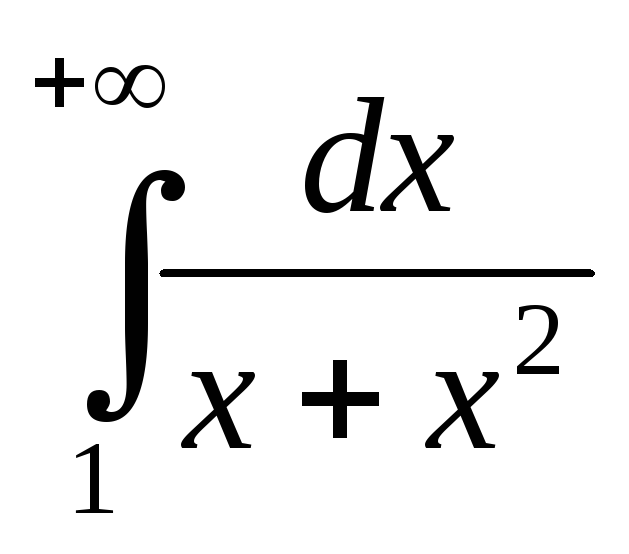 ;
;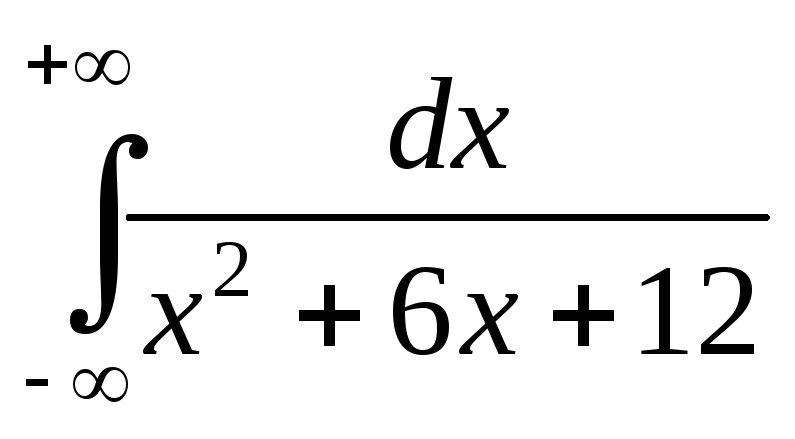 ;
;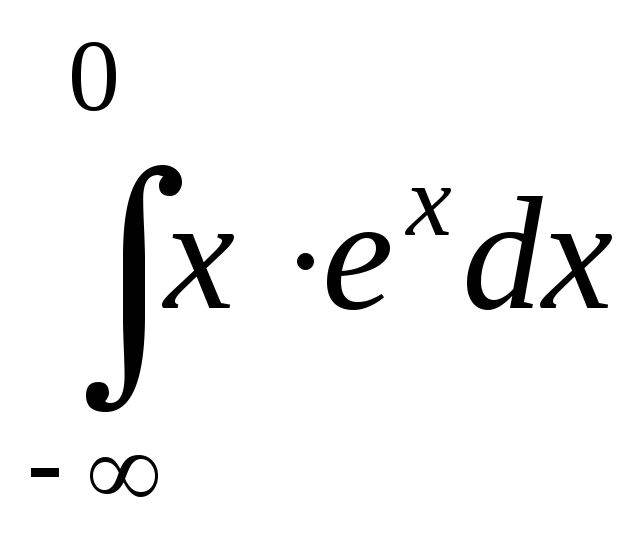 ;
;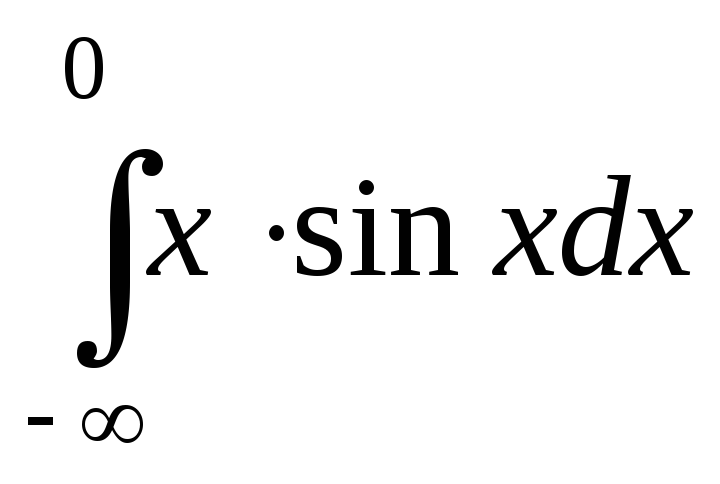 ;
;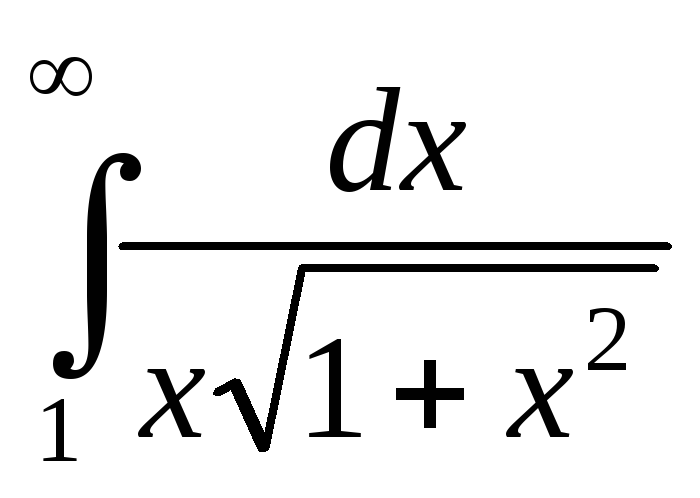 ;
;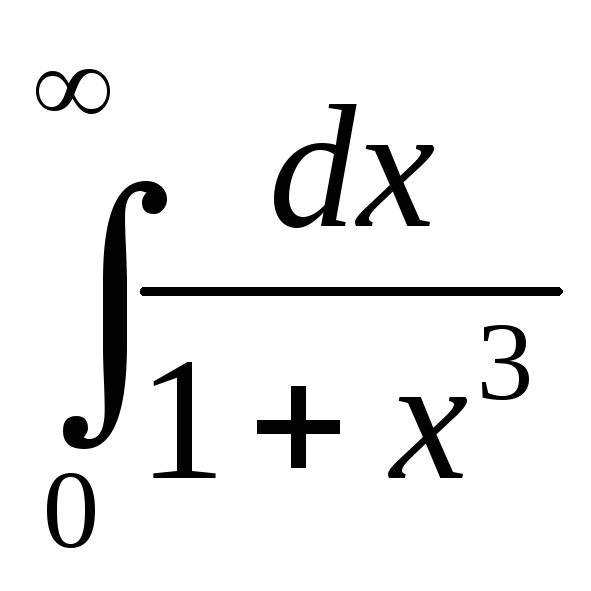 ;
;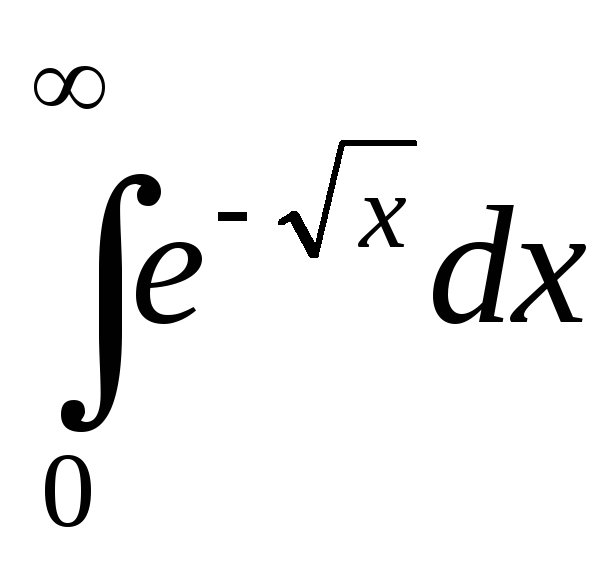 ;
;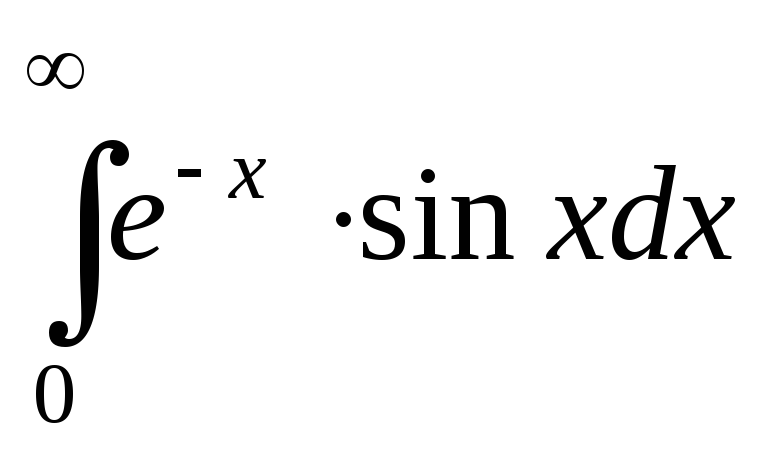 ;
;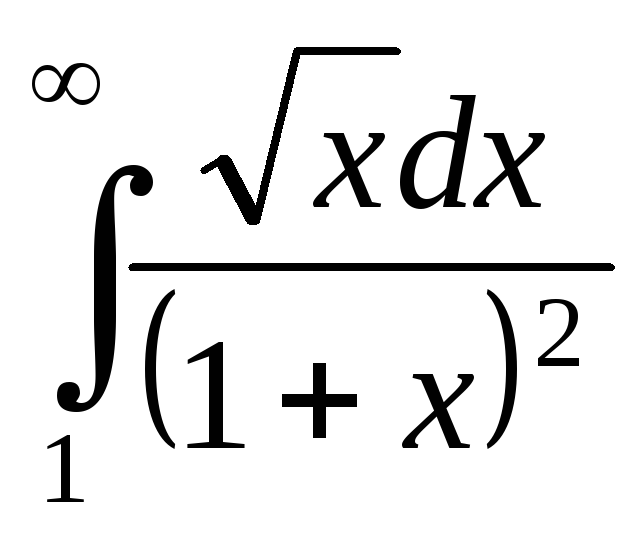 ;
;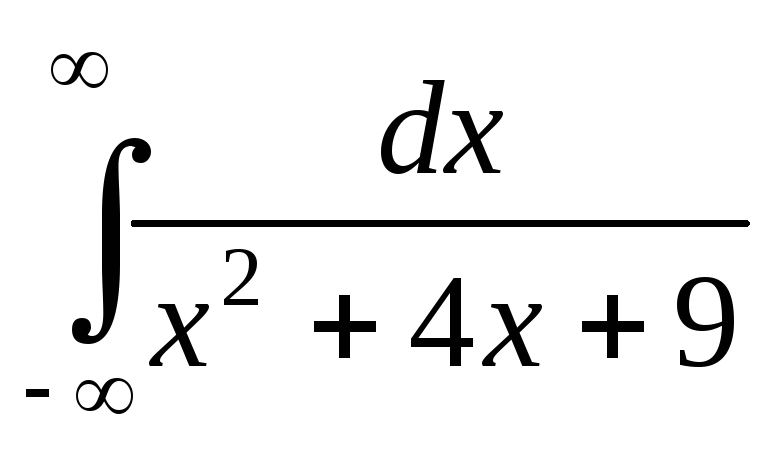 .
.
II. Вычислить интегралы от неограниченных функций или установить их расходимость:
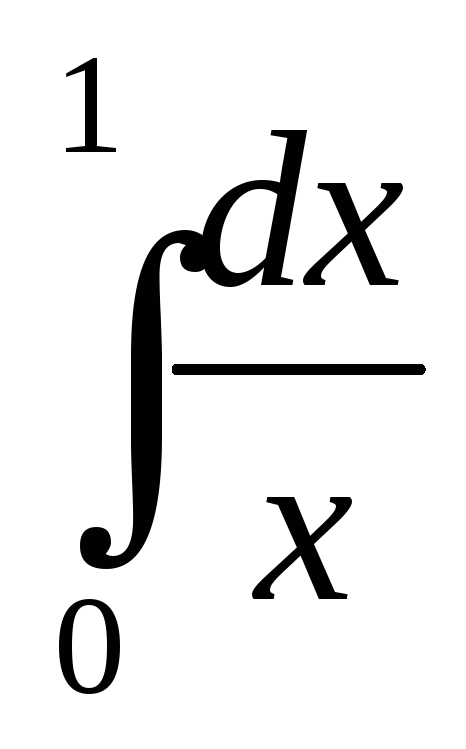 ;
;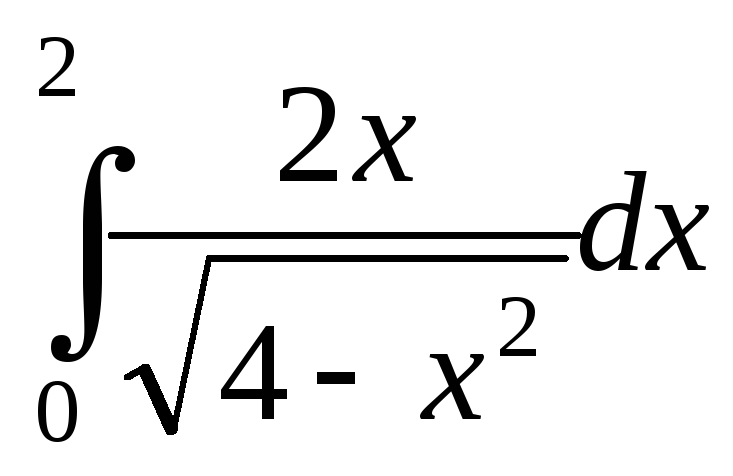 ;
;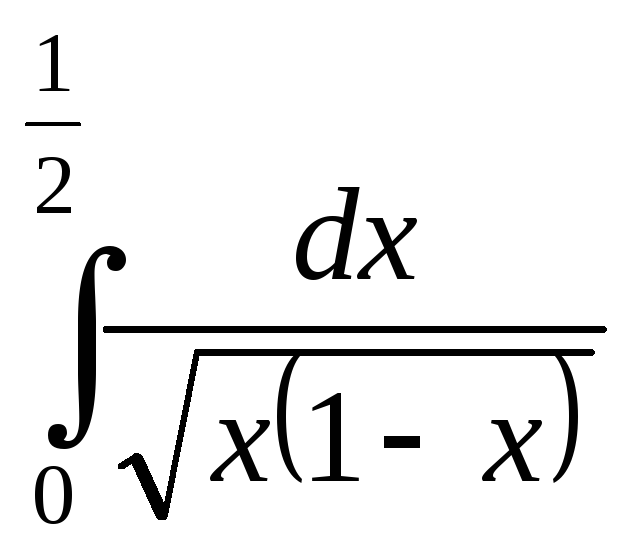 ;
;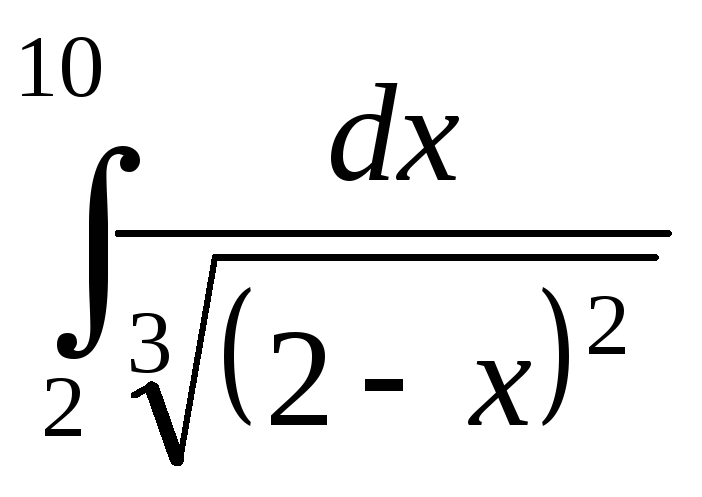 ;
;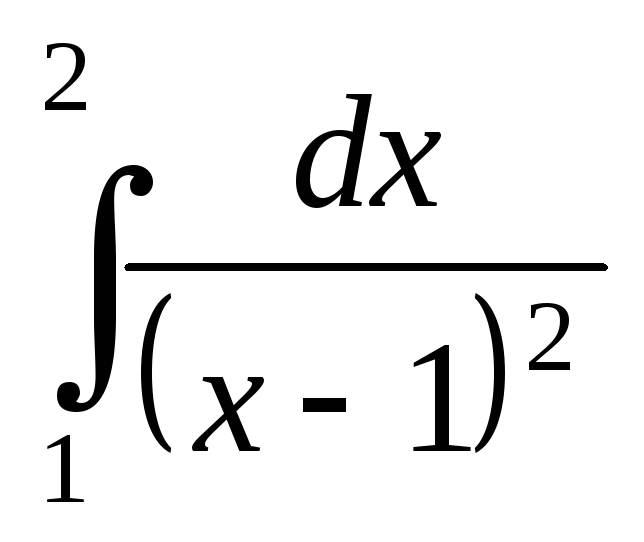 ;
; ;
; ;
;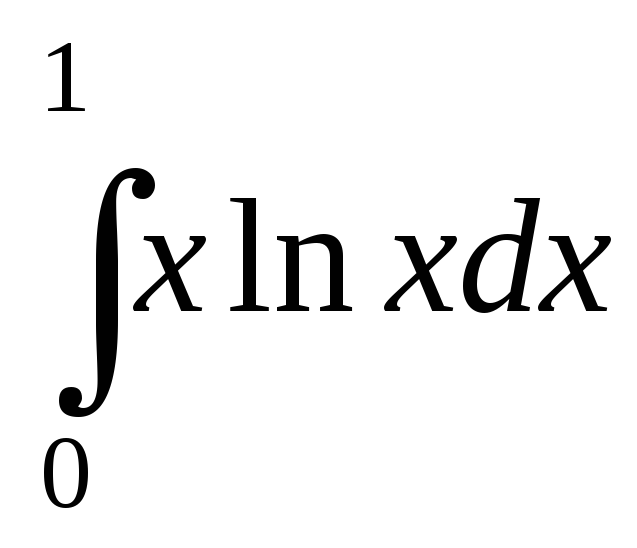 ;
;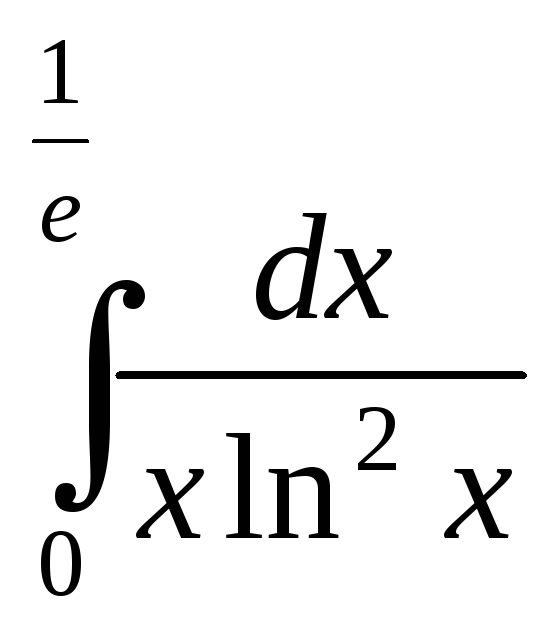 ;
;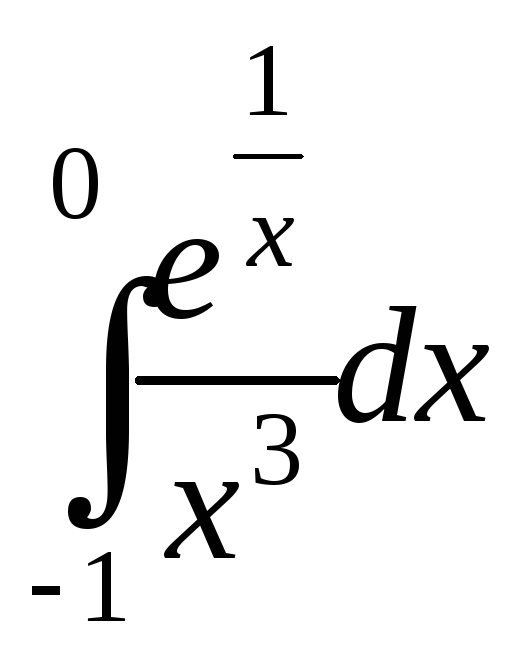 ;
;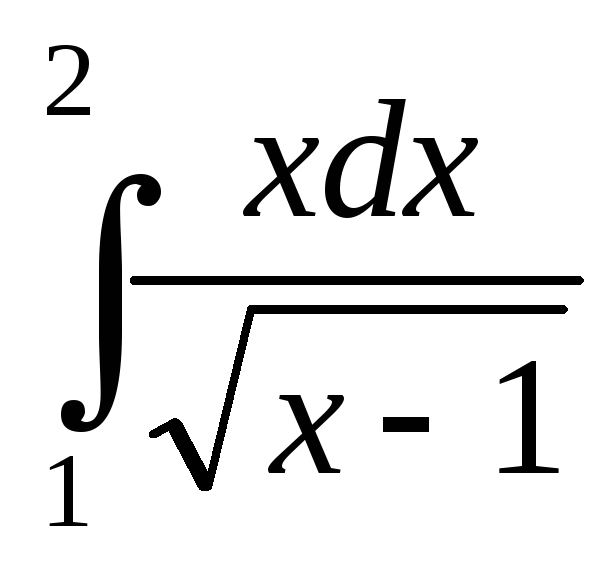 ;
;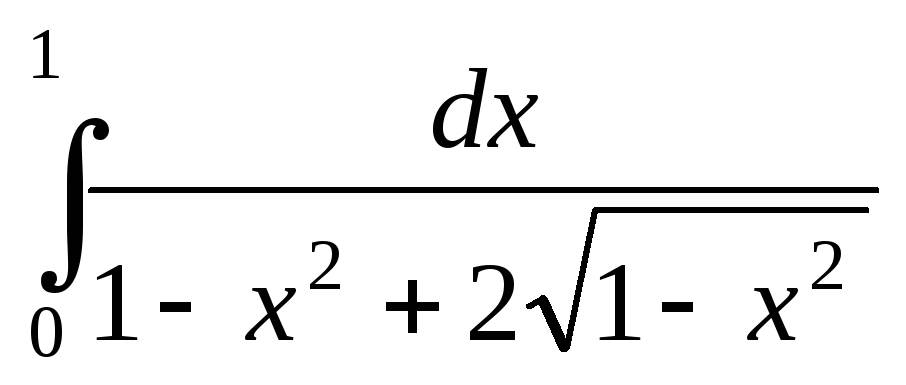 ;
;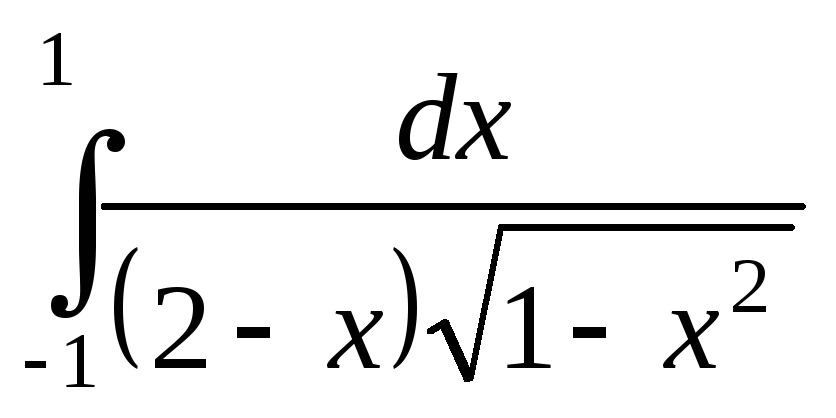 ;
;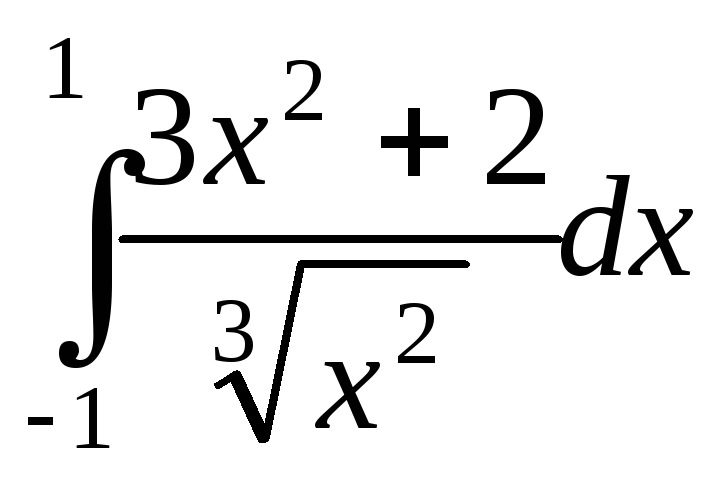 ;
; ;
;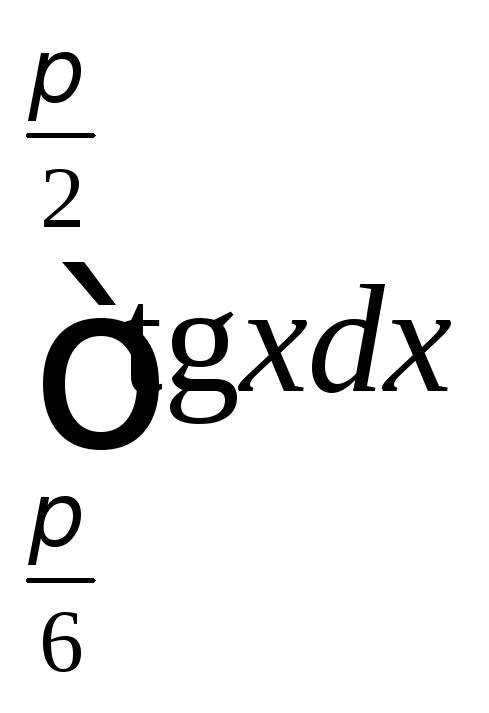 ;
;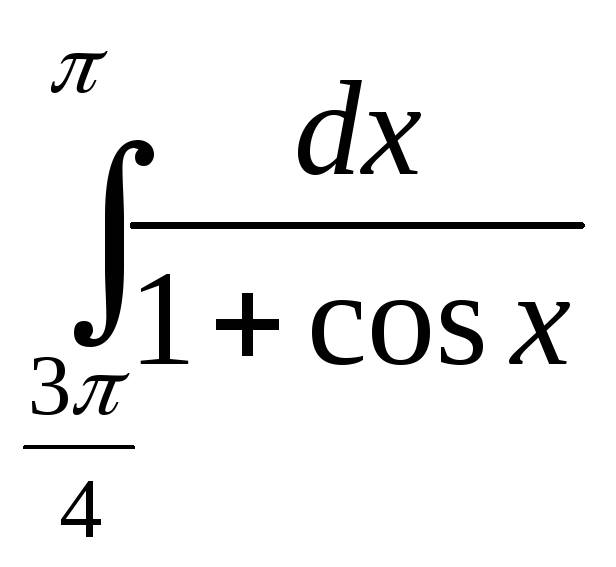 ;
;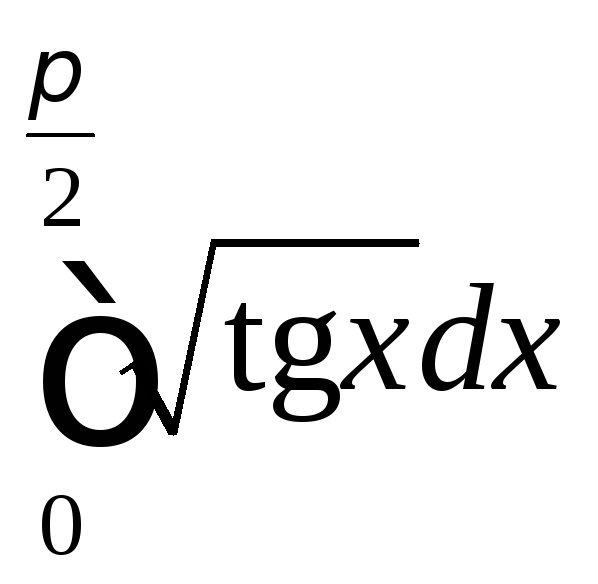 .
.
Тема 6. Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур
Вопросы для повторения:
Площадь криволинейной трапеции в прямоугольной системе координат.
Площадь плоской фигуры в полярной системе координат.
Площадь криволинейной трапеции, ограниченной кривой, заданной в параметрической форме.
Пример 1. Найти площадь фигуры, ограниченной линиями:
y=x+ 2,y2= 9x
Построим графики и найдем точки пересечения этих линий. Для этого решим систему:
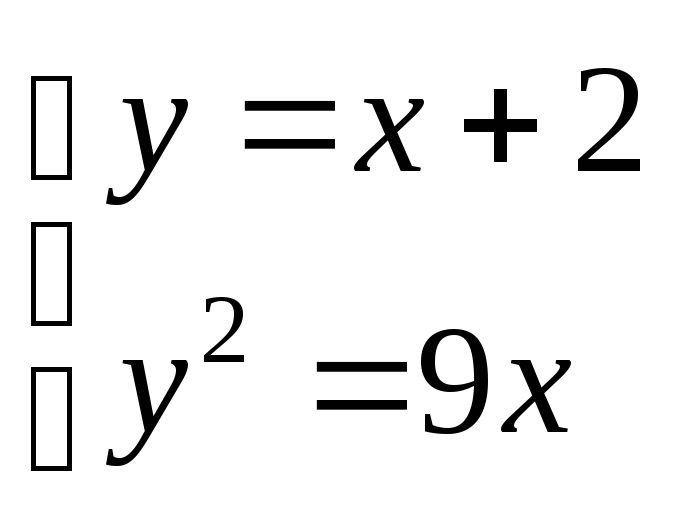 .
.
Откуда
![]() или
или
![]() .
.
Точки пересечения х1= 4,х2= 1.
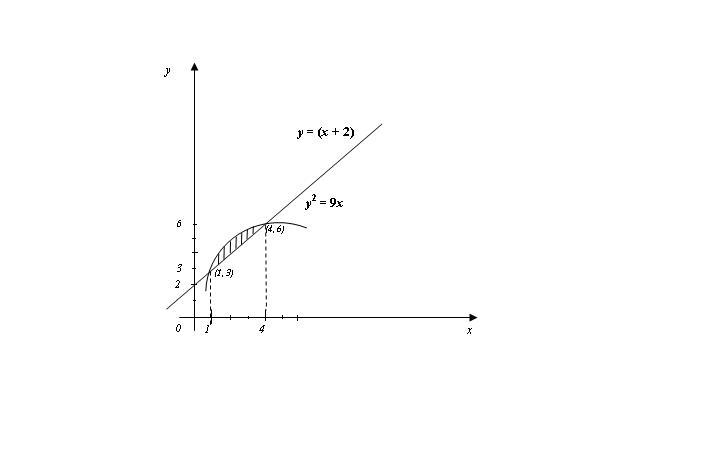
Тогда
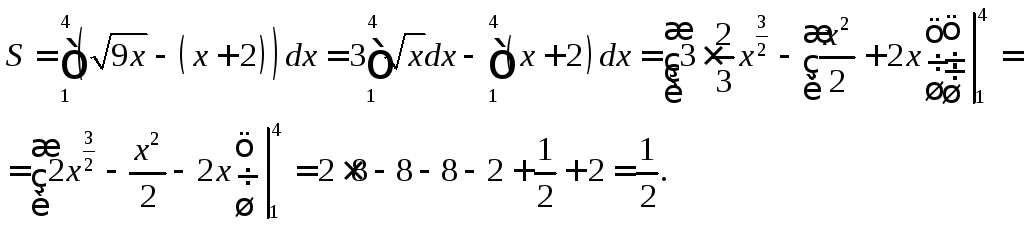
Найдем координаты точки пересечения
гиперболы
![]() и параболы
и параболы![]() ,
решая систему:
,
решая систему:
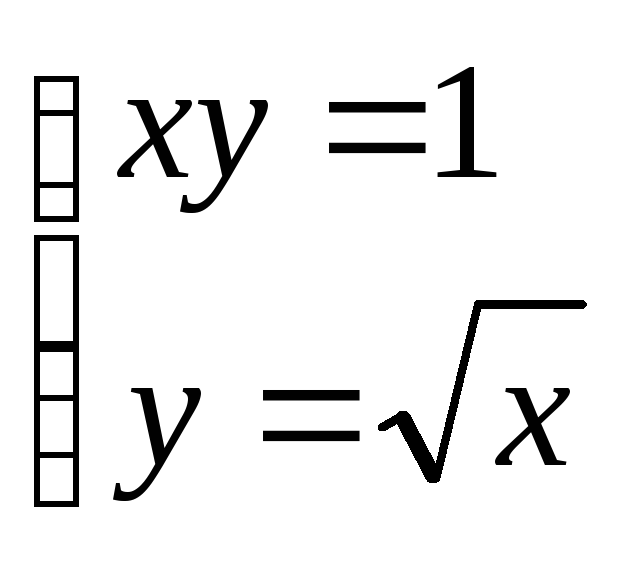 ,
откуда
,
откуда![]() илиx= 1,y= 1.
илиx= 1,y= 1.
Построим график:

Так криволинейная трапеция сверху ограничена разными кривыми, то разобьем промежуток интегрирования на два промежутка: от 0 до 1 и от 1 до 4. Тогда
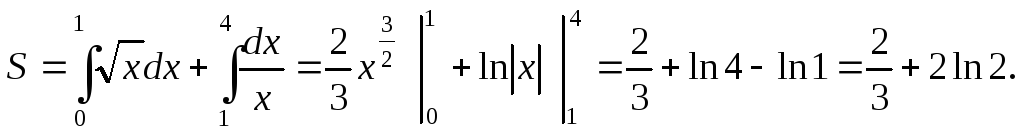
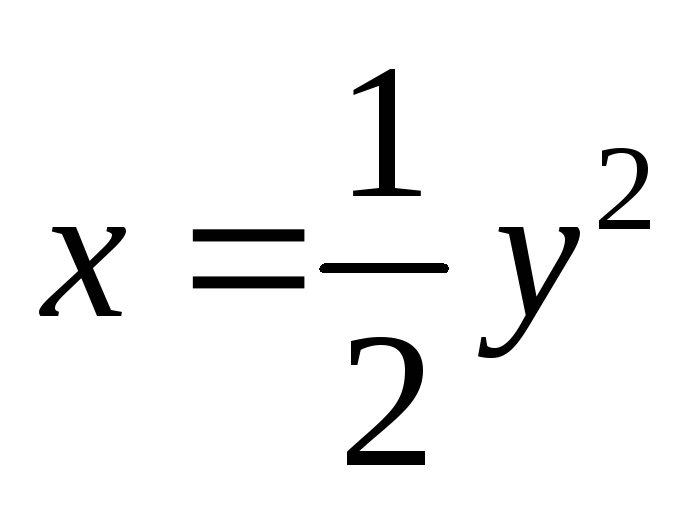 ,
осью ординат и прямымиy= 1,y= -3. Сделаем
чертеж.
,
осью ординат и прямымиy= 1,y= -3. Сделаем
чертеж.
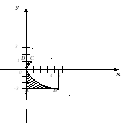
Площадь криволинейной трапеции ABCDбудет:
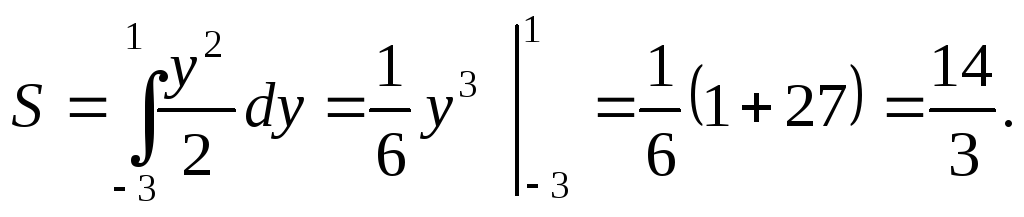
Пример 2. Найти площадь фигуры, заданной параметрически:
эллипсом x = a cos t, y = b sin t

Оси координат делят эллипс на четыре одинаковых части. Найдем площадь, расположенную в первом квадранте:
![]()
Преобразуем интеграл по переменной t.
Прих= 0,![]() ,
а прих=а,t
= 0;
,
а прих=а,t
= 0;![]() .
.
Тогда
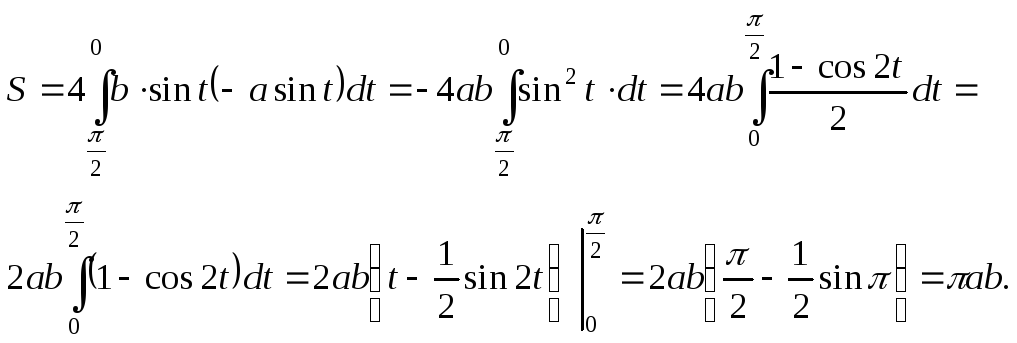
одной аркой циклоиды
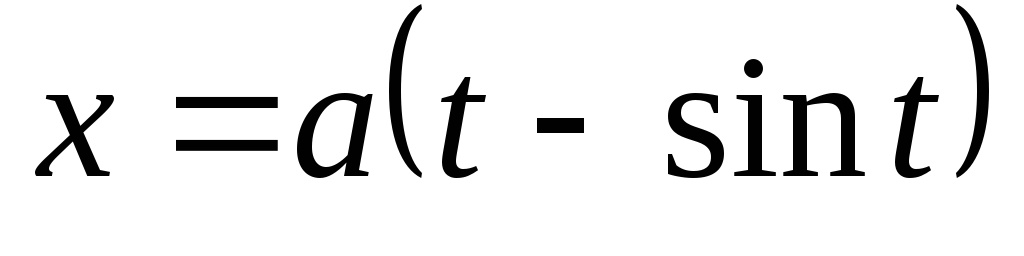 ,
, и осьюох
и осьюох


Найдем площадь по формуле
![]()
Если х= 0, тоt =
0, еслих= 2πа, то t
=2π,![]() .
.
Отсюда имеем:
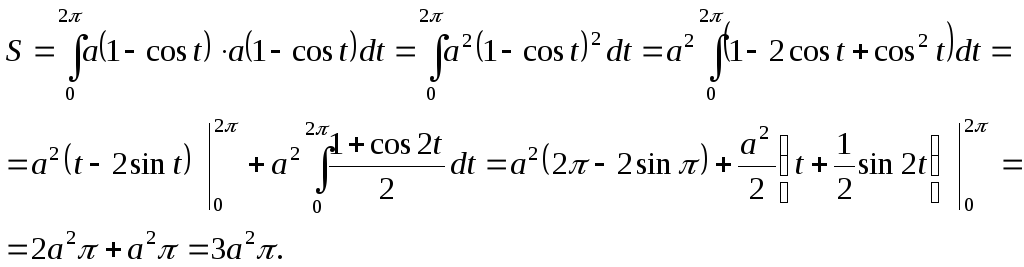
Пример 3. Найти площадь, ограниченную линиями:
лемнискатой Бернулли
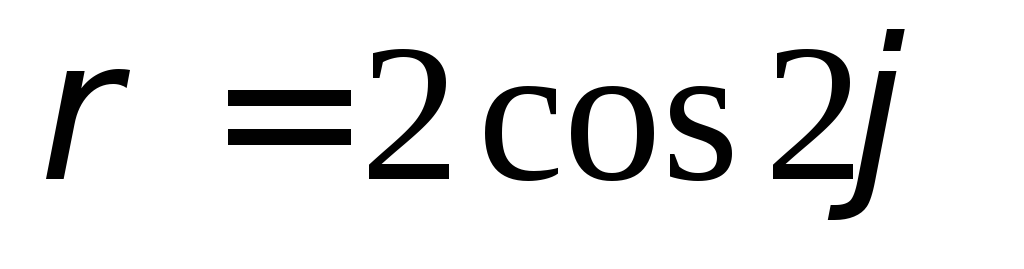
Так как
![]() ,
то
,
то![]() ,
тогда находим
,
тогда находим![]()

Так как фигура состоит из четырех одинаковых частей, имеем:
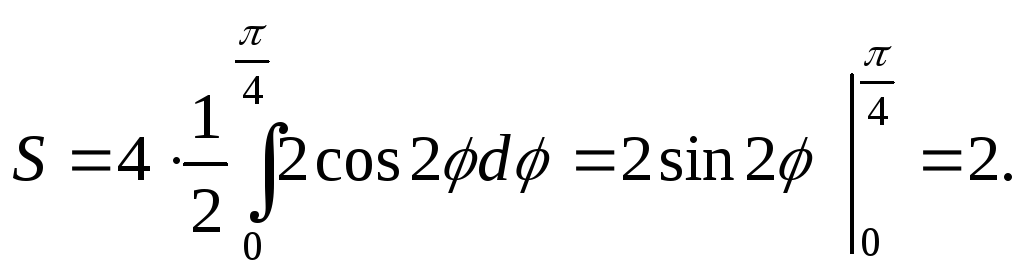
окружностями
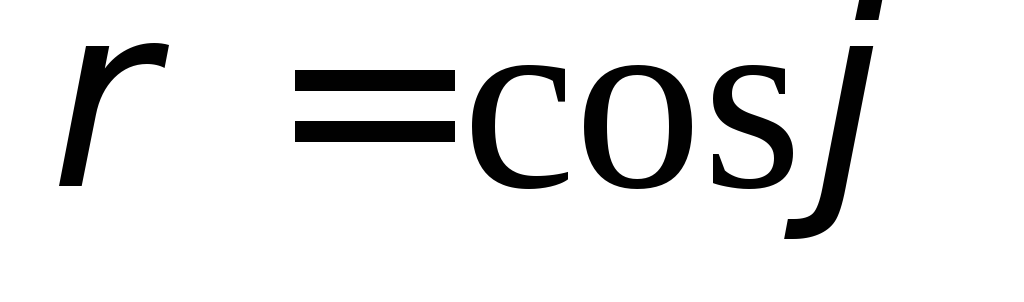 и
и
Решаем совместно уравнения окружностей:
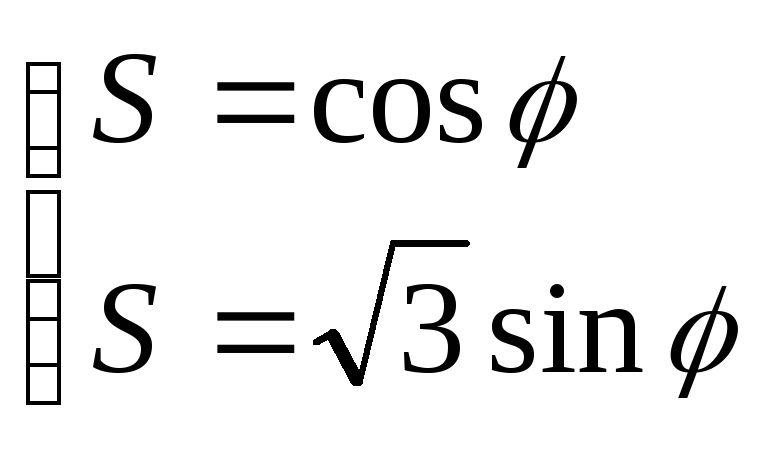 или
или
![]() ,
,![]() ,
,
учитывая, что
![]() ,
,![]() ,
получим
,
получим![]() ,
,![]() .
.
Т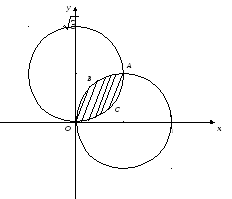 очка
пересечения А
очка
пересечения А![]() .
.
Искомая площадь равна сумме площадей двух сегментов ОВА и ОСА.
Дуга ОСА описывается концом
полярного угла φ
от 0 до
![]() ,
следовательно,
,
следовательно,

Дуга ОВА описывается концом
полярного радиуса меньшей окружности
при изменении φ от
![]() до
до![]() ,
следовательно,
,
следовательно,
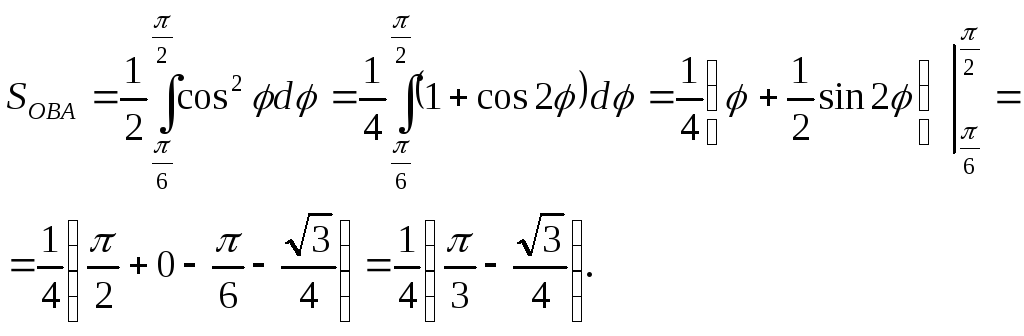
Таким образом, искомая площадь
![]()