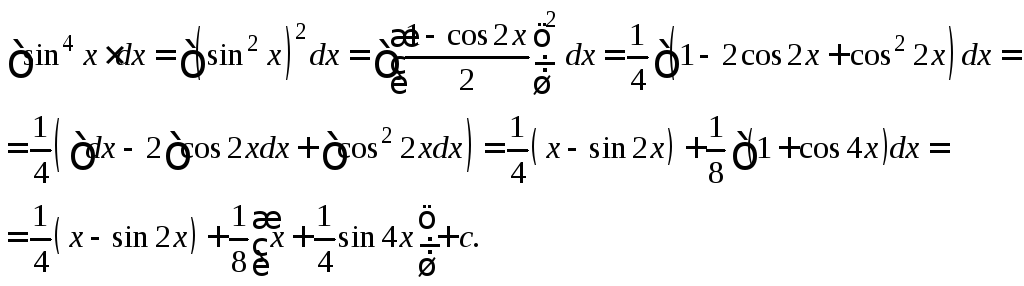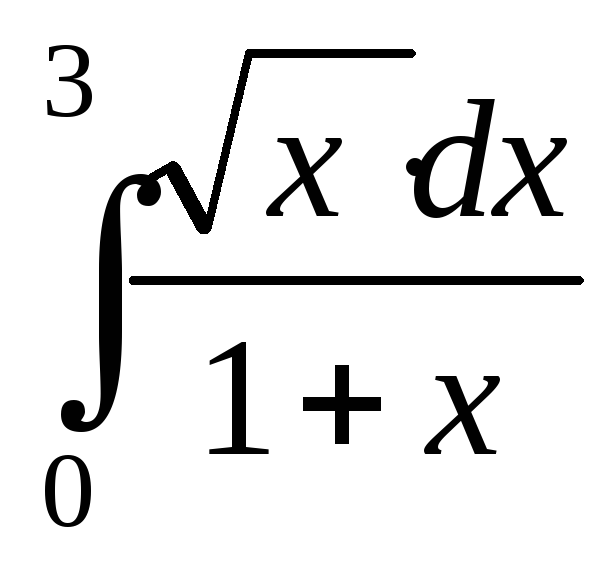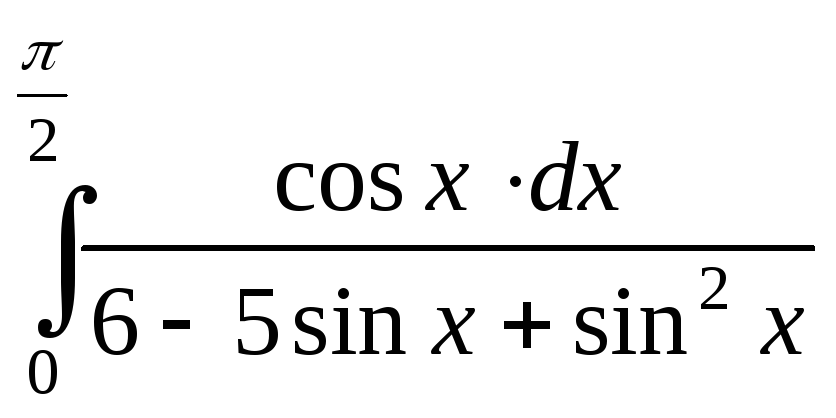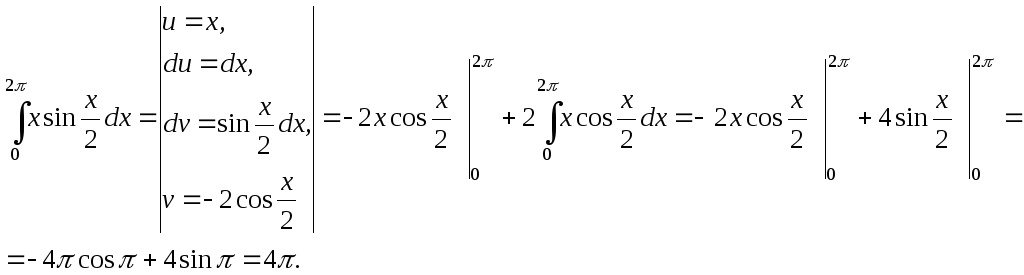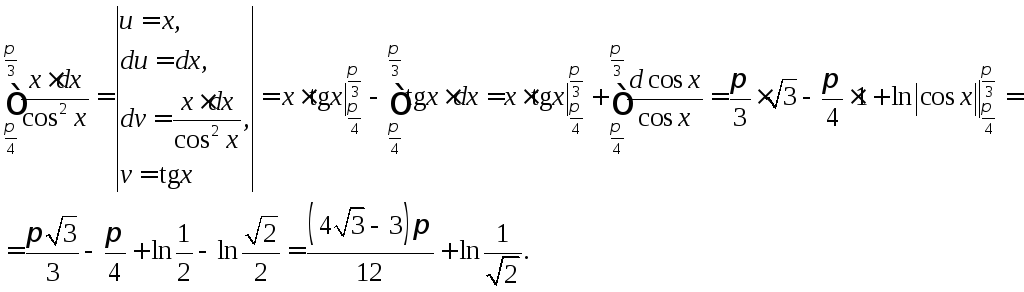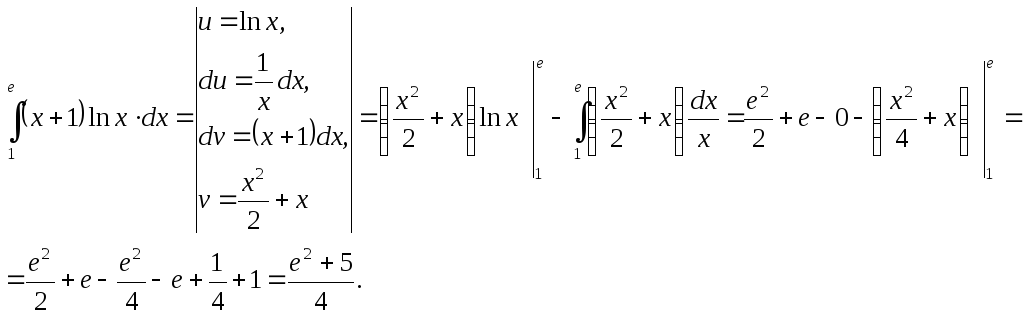- •Тема 1. Неопределенный интеграл
- •Задания для самостоятельного решения
- •Тема 2. Интегрирование рациональных функций
- •Задачи для самостоятельного решения
- •Тема 3. Интегрирование иррациональных функций
- •Задачи для самостоятельного решения
- •Тема 4. Интегрирование тригонометрических функций
- •Задачи для самостоятельного решения
- •Тема 5. Определенный интеграл
- •Задачи для самостоятельного решения
- •Тема 6. Несобственные интегралы
- •Задачи для самостоятельного решения
- •Тема 6. Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур
- •Задачи для самостоятельного решения
- •Тема 8. Приложения определенного интеграла. Вычисление длины дуги кривой
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
Разложить правильную рациональную дробь на простейшие дроби:
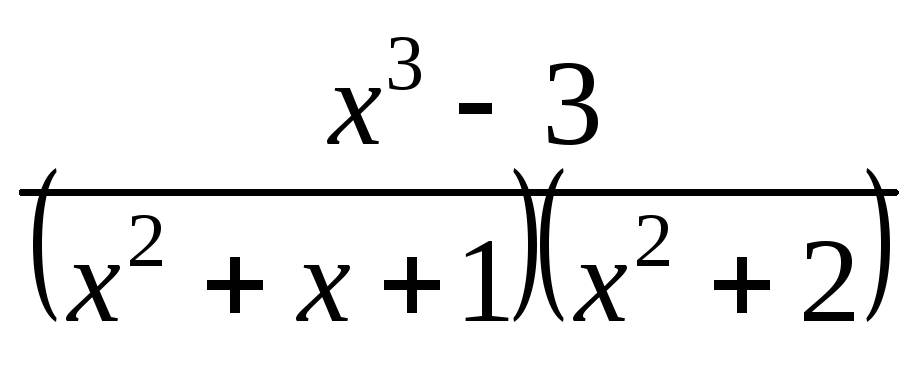 ;
;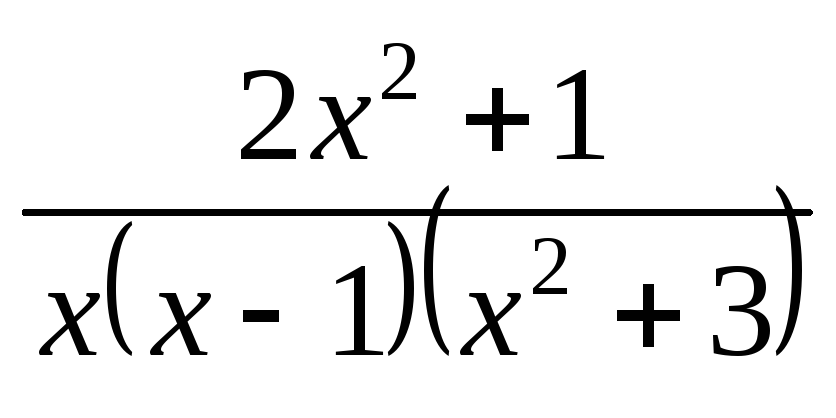 ;
;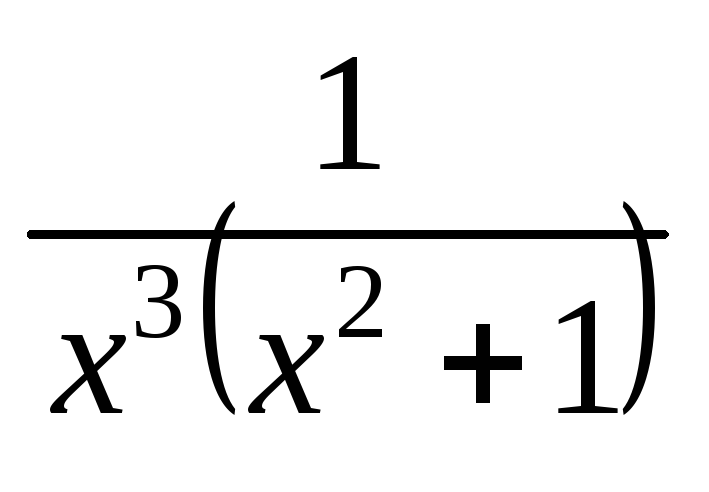 ;
;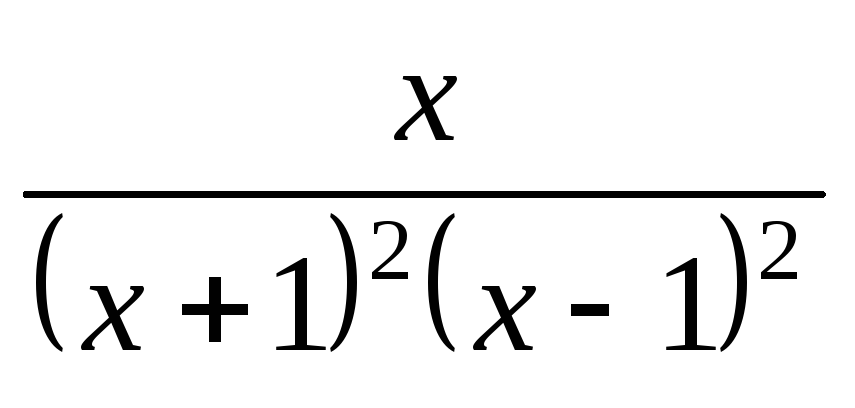 ;
;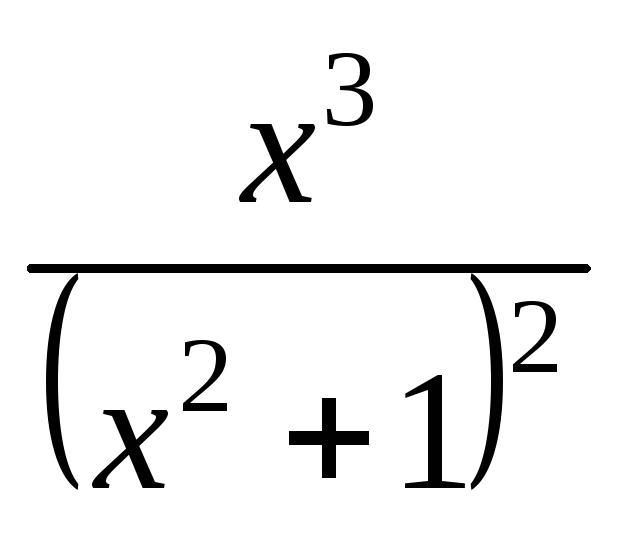 .
.
Найти интегралы от простейших дробей:
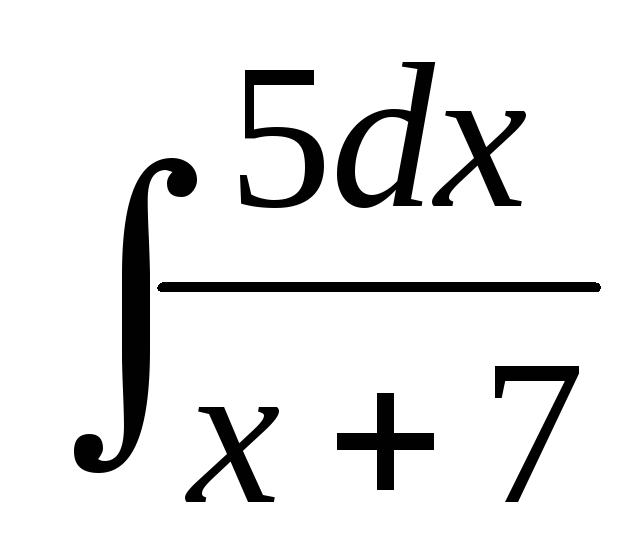 ;
;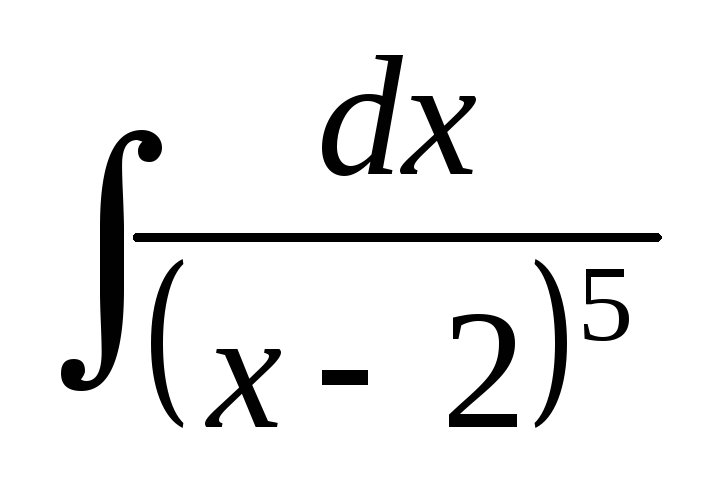 ;
;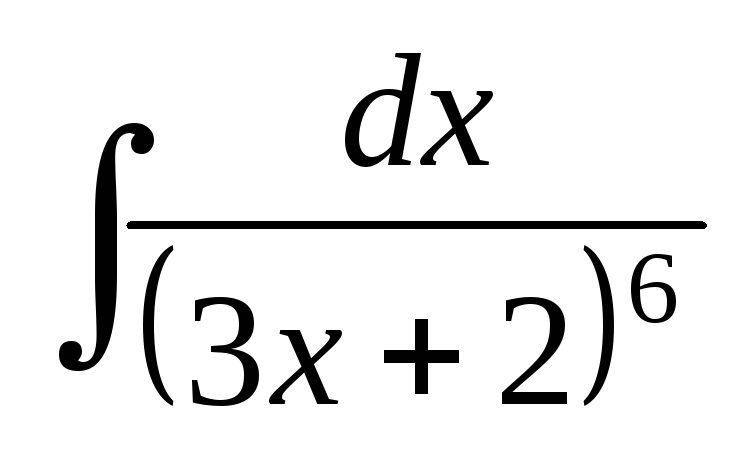 ;
;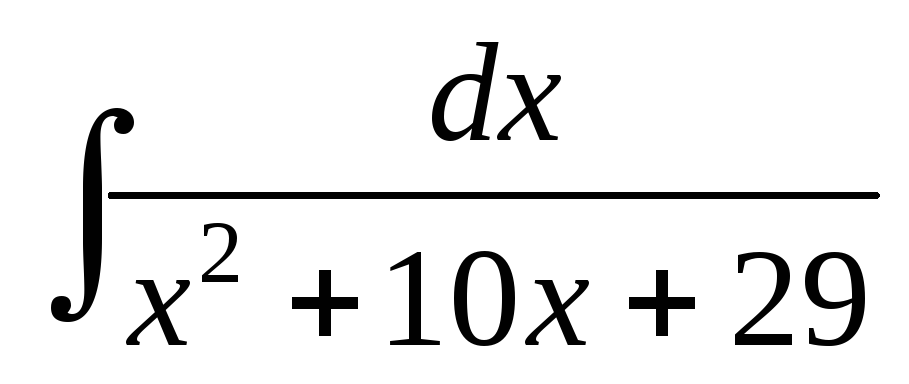 ;
;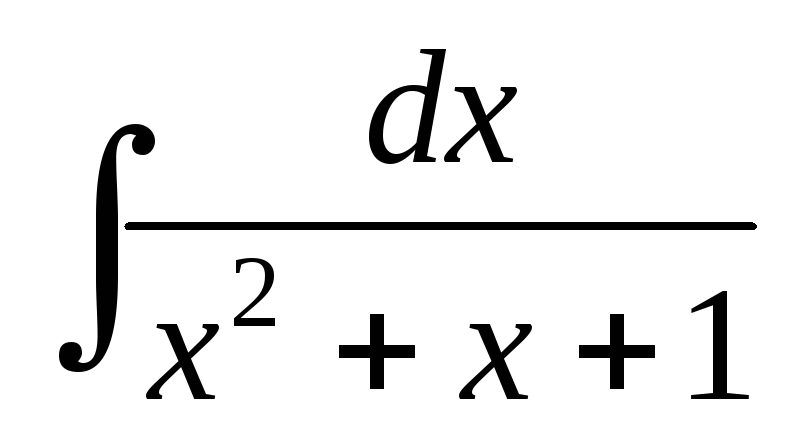
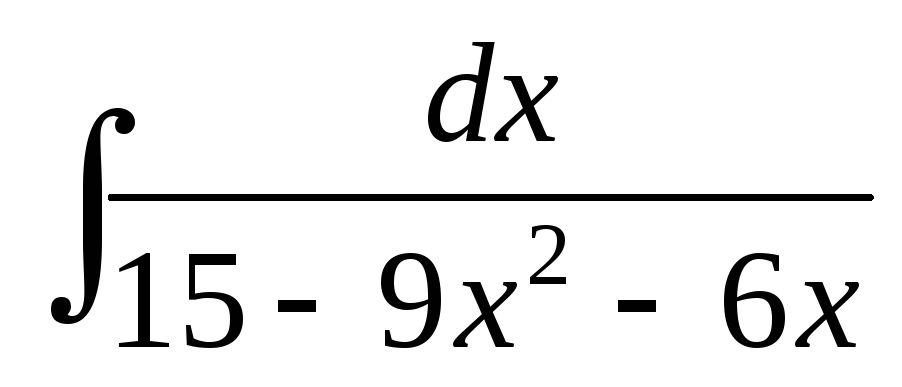 ;
;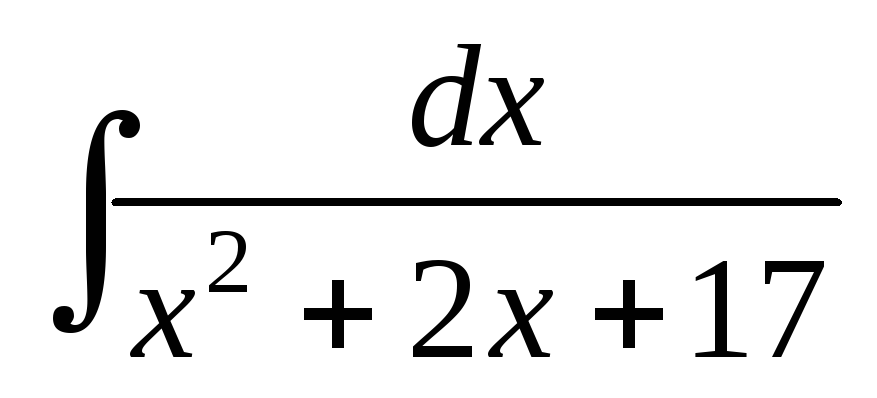 ;
;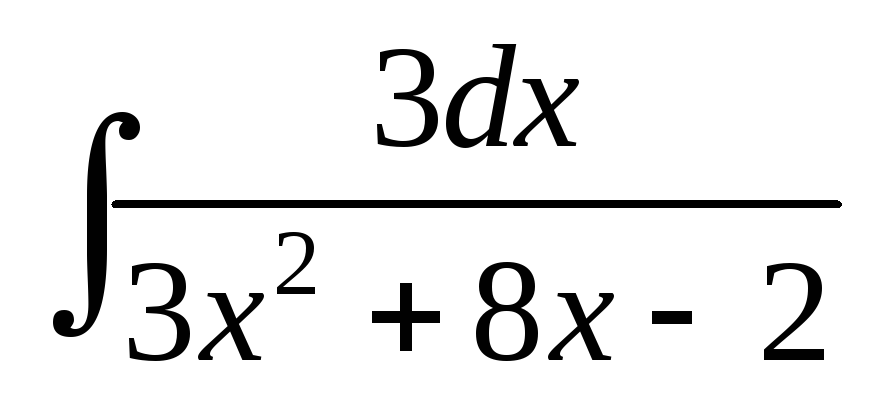 ;
;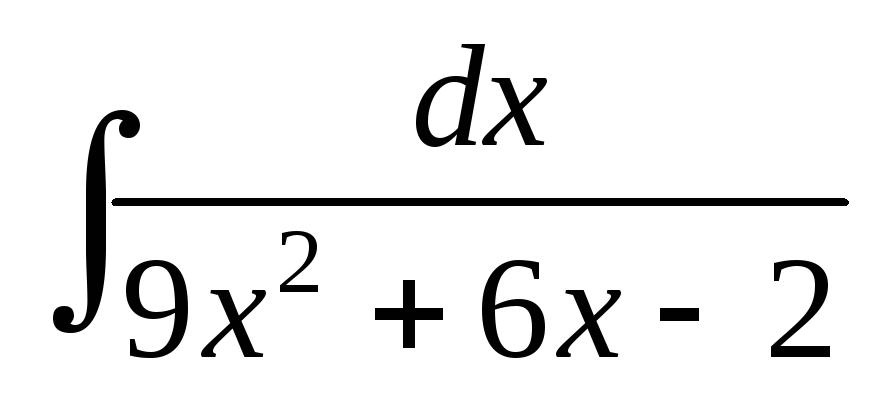 ;
;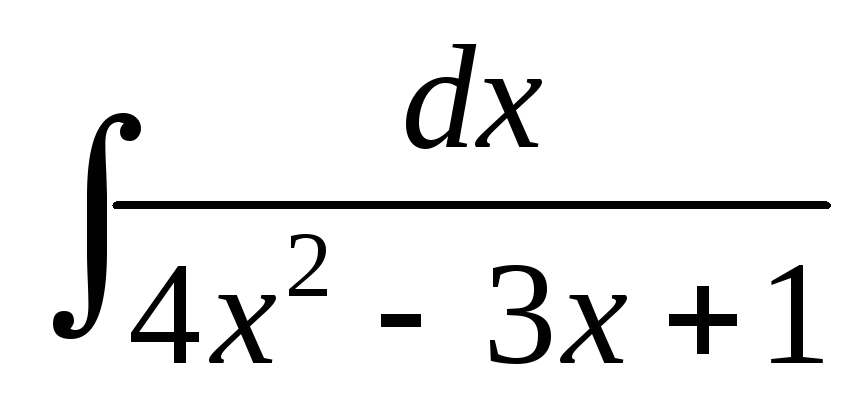 ;
; ;
;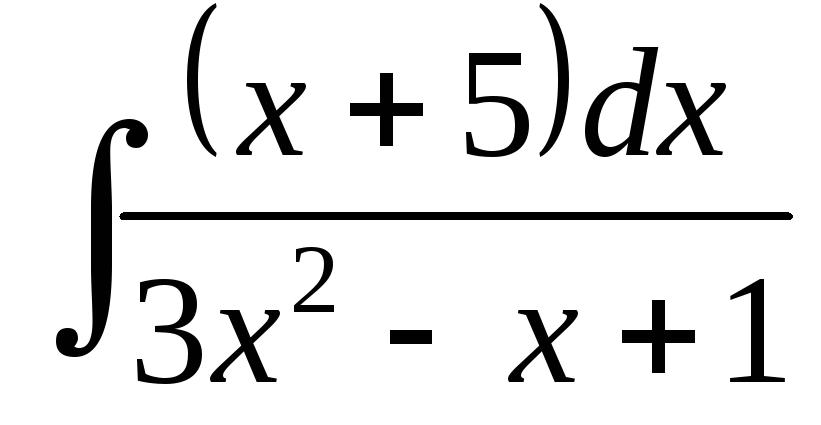 ;
;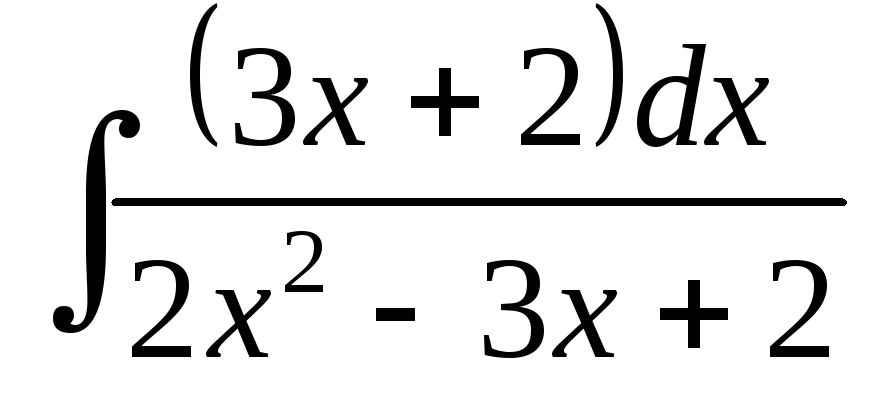 ;
;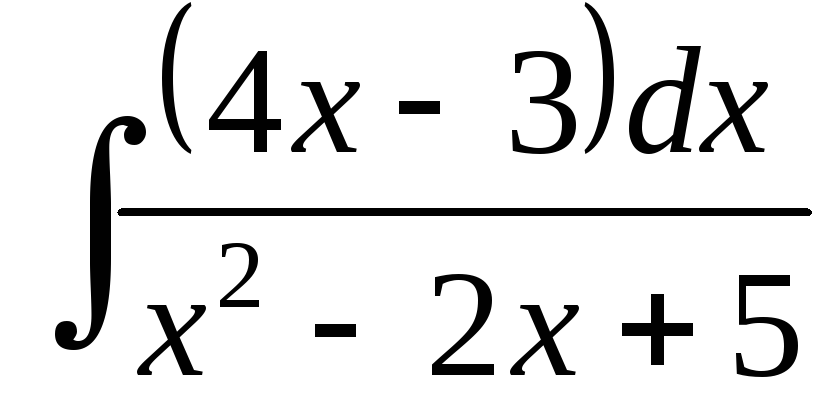 ;
;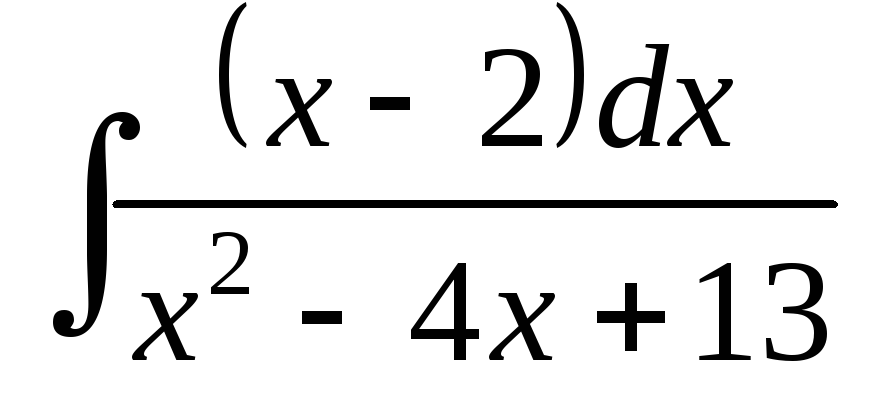 ;
;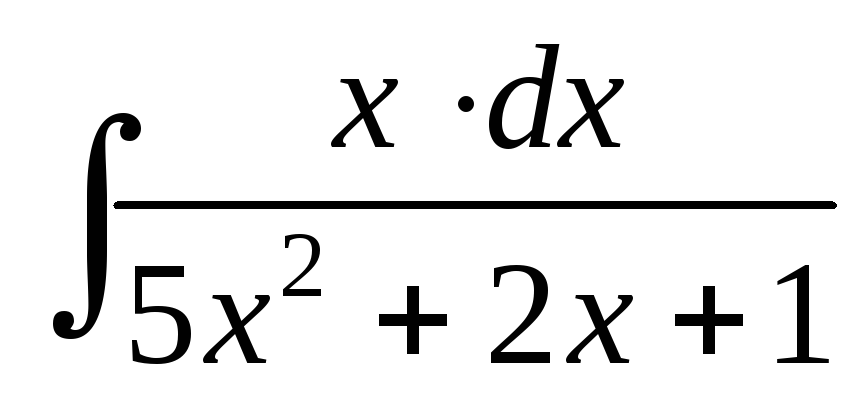 ;
;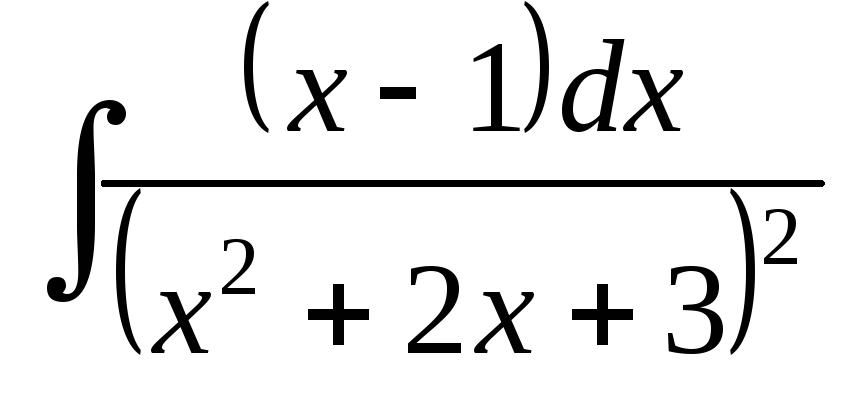 ;
;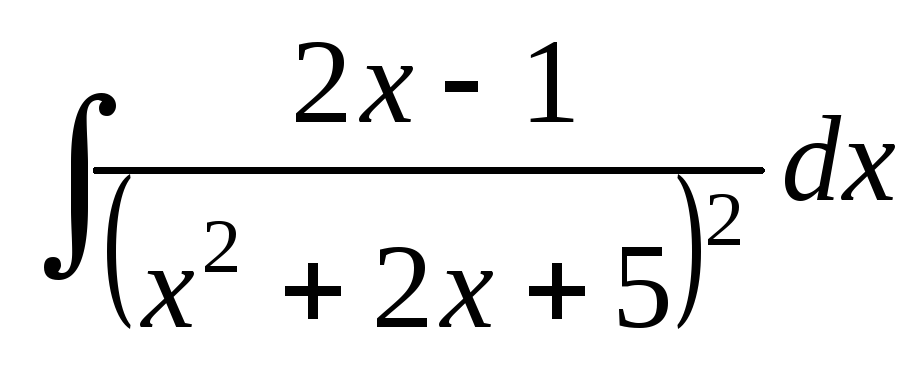 ;
;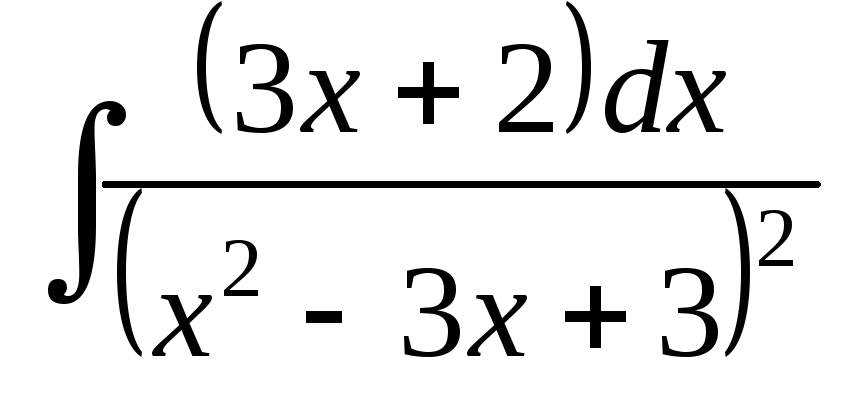 .
.
Найти интегралы:
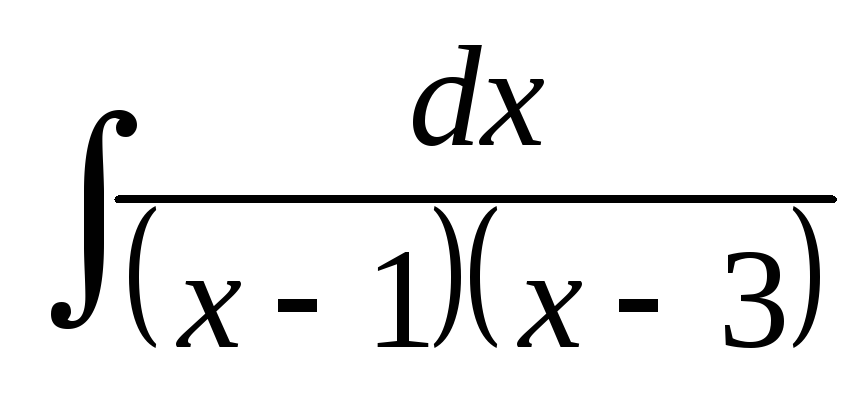 ;
;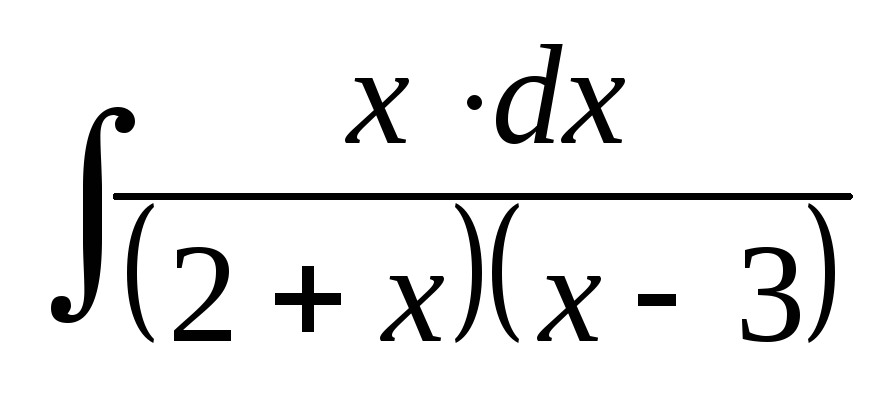 ;
;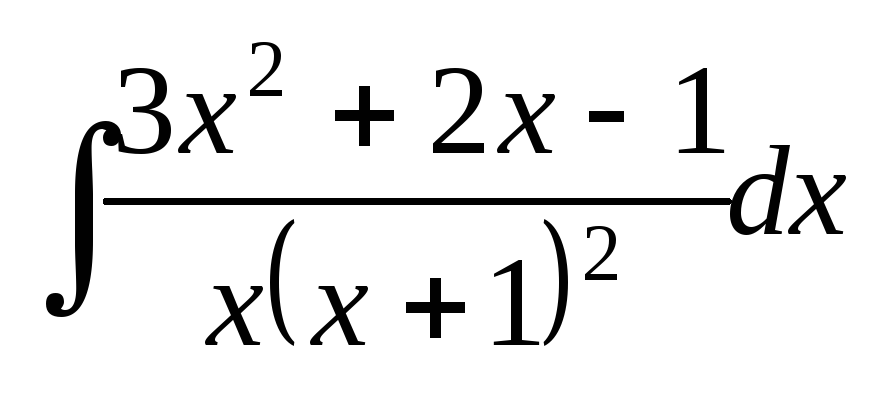 ;
;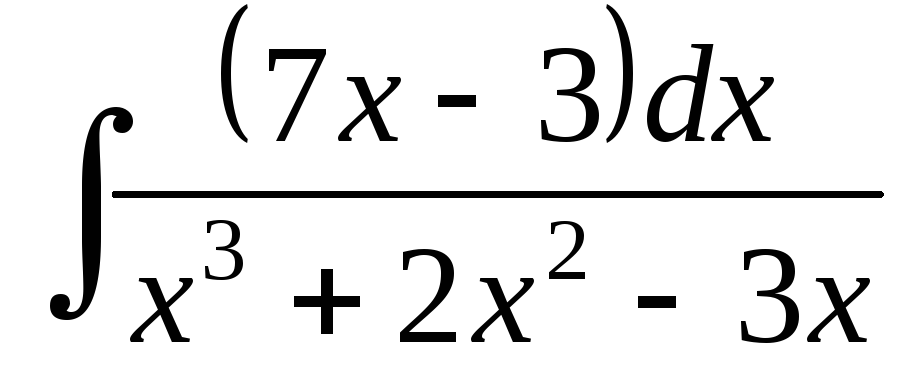 ;
;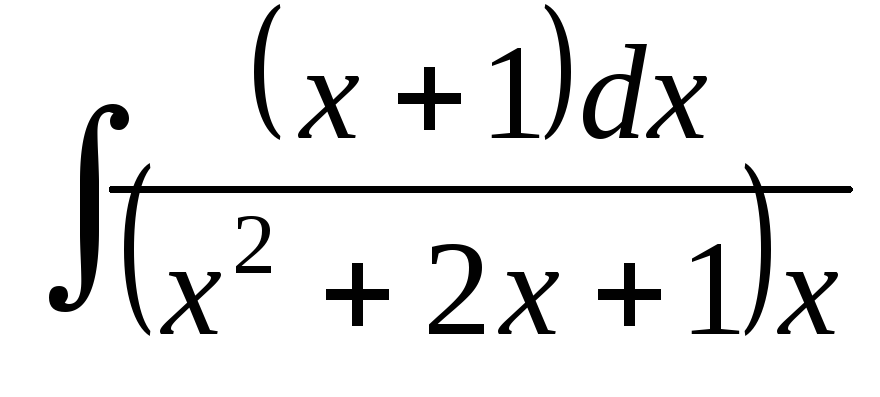 ;
;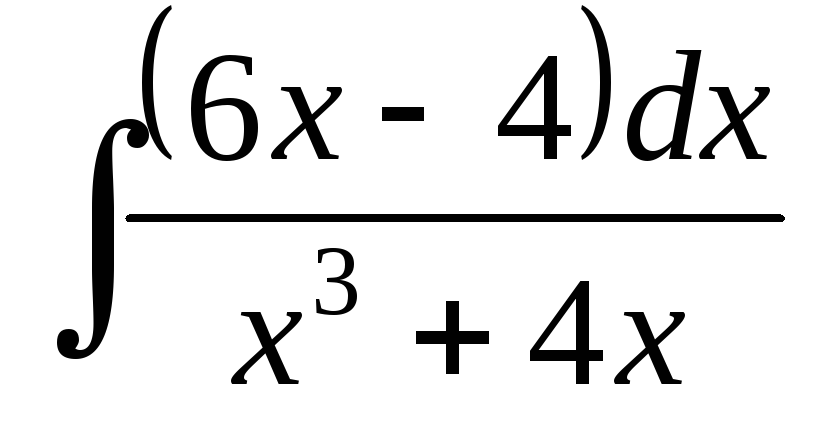 ;
;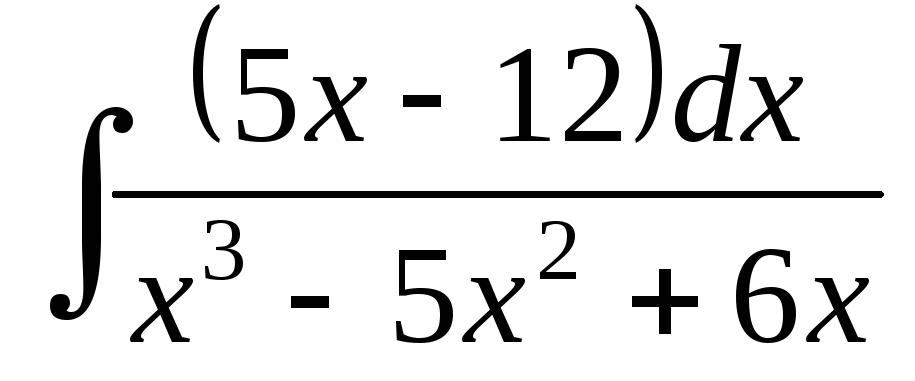 ;
;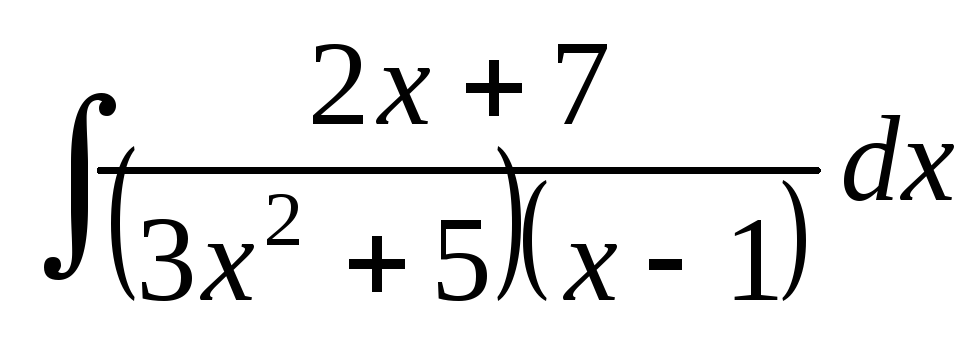 ;
;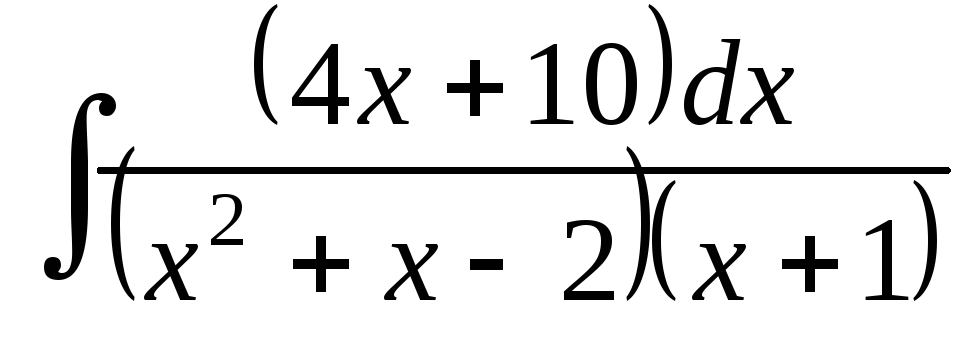 ;
;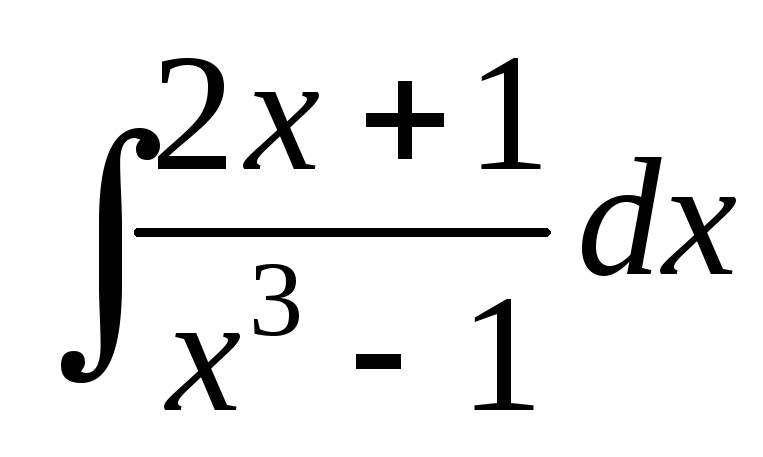 ;
; ;
;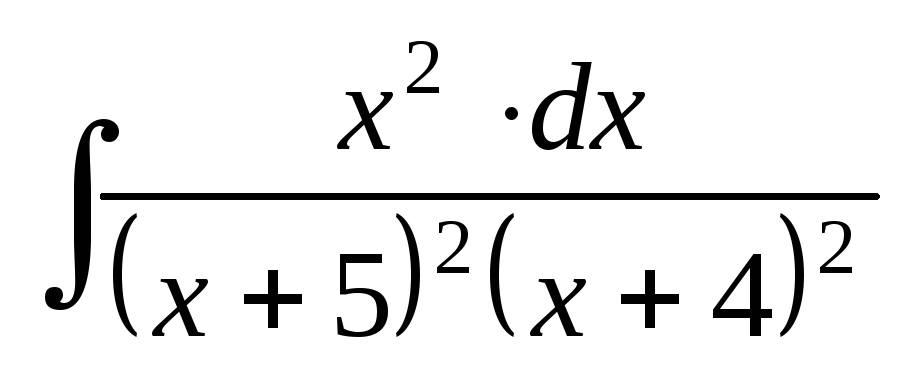 ;
;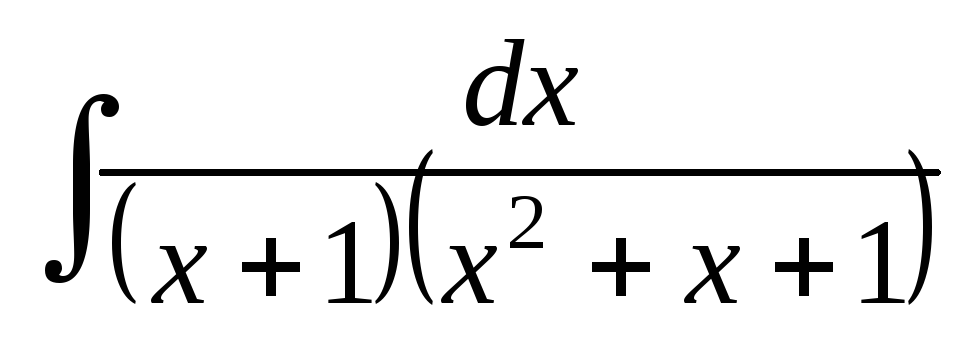 ;
;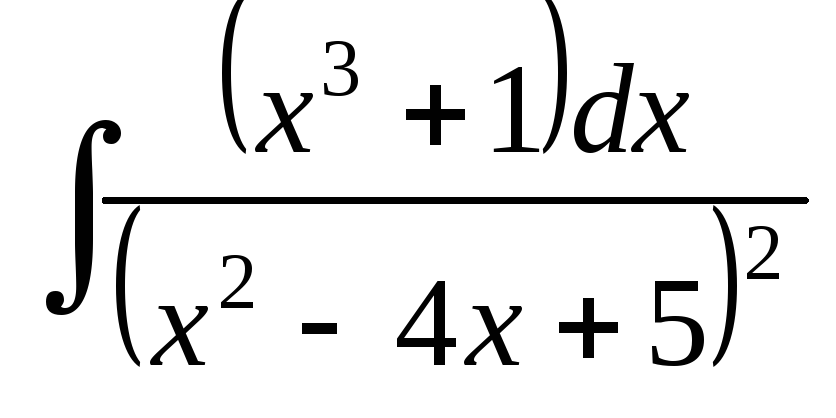 ;
;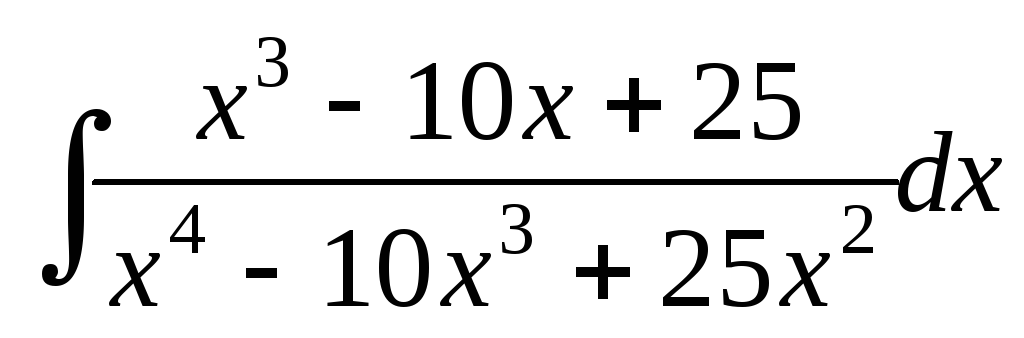 ;
;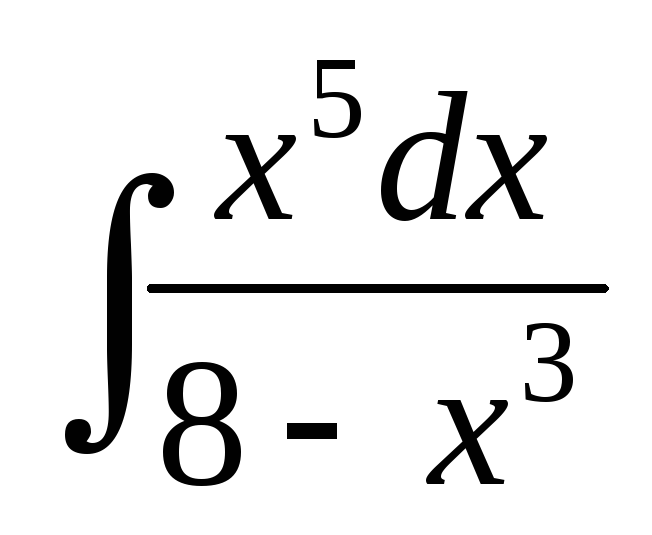 ;
;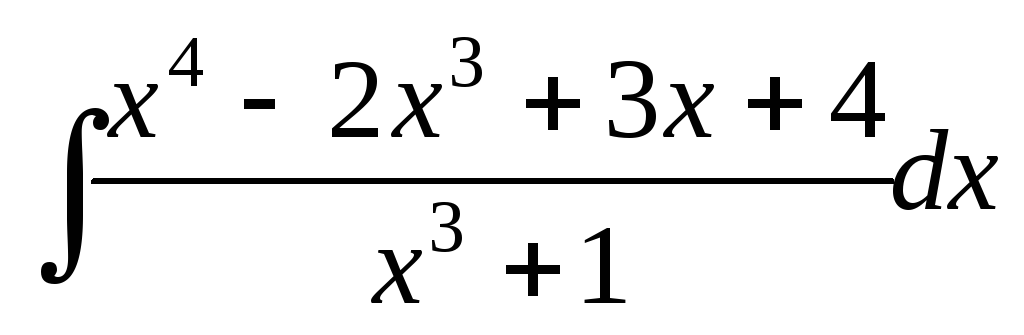 ;
;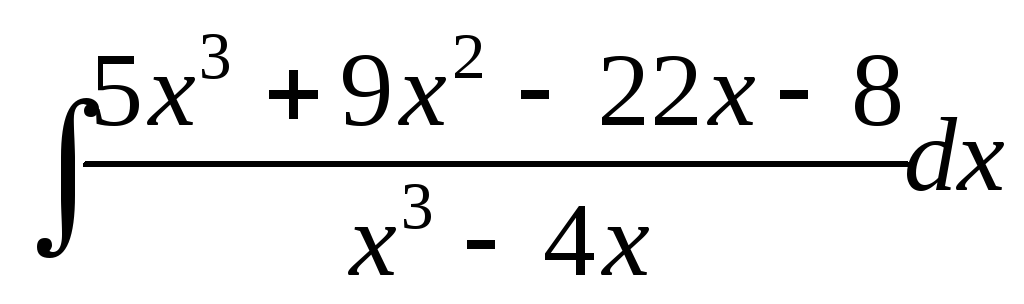 ;
;
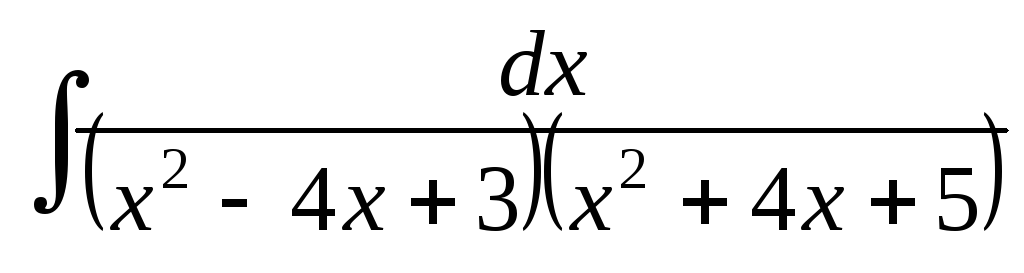 ;
;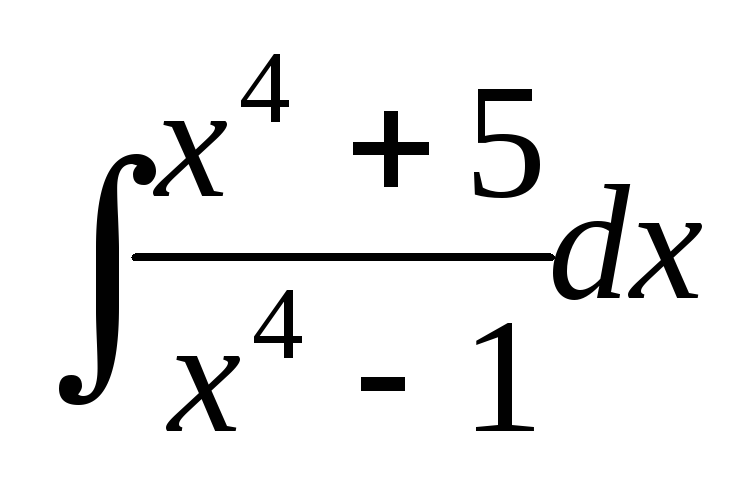 ;
;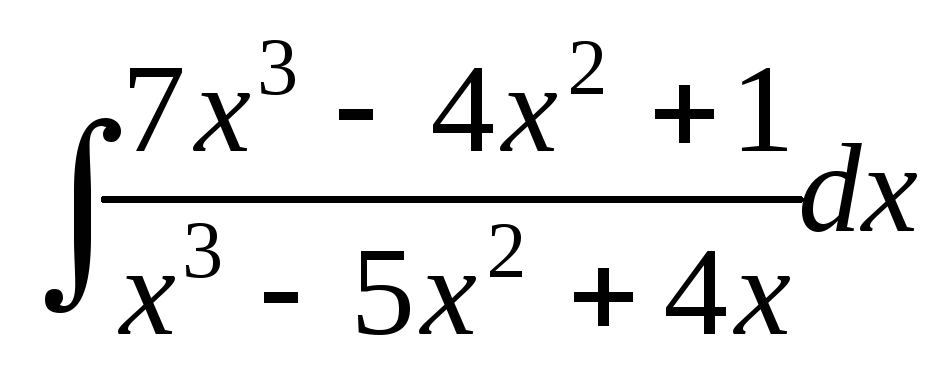 ;
;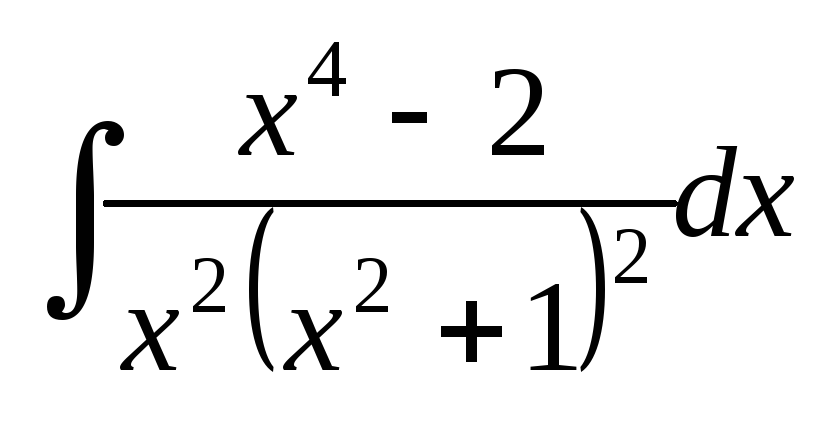 ;
;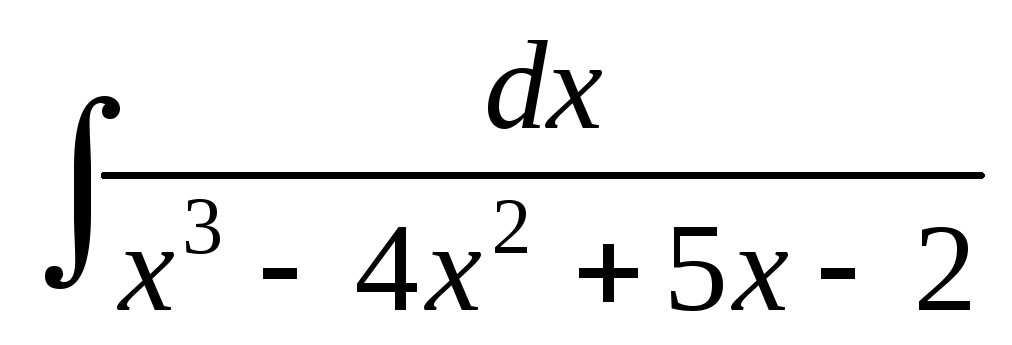 ;
;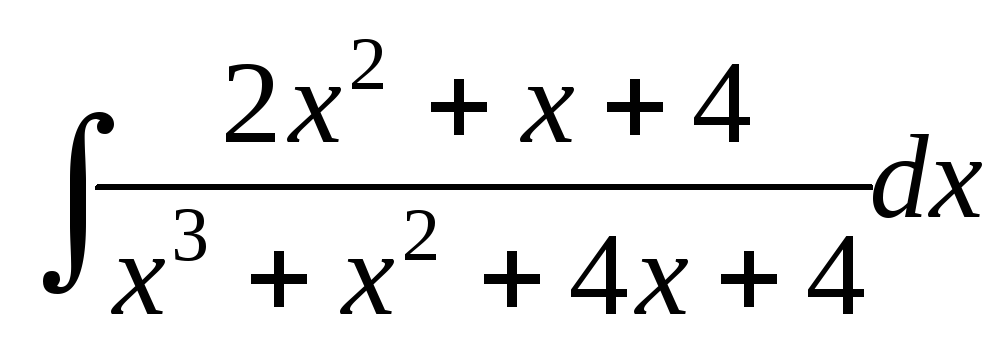 ;
;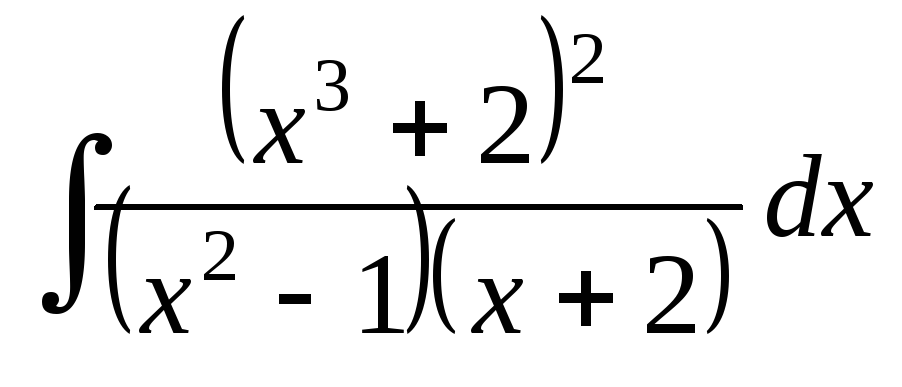 ;
;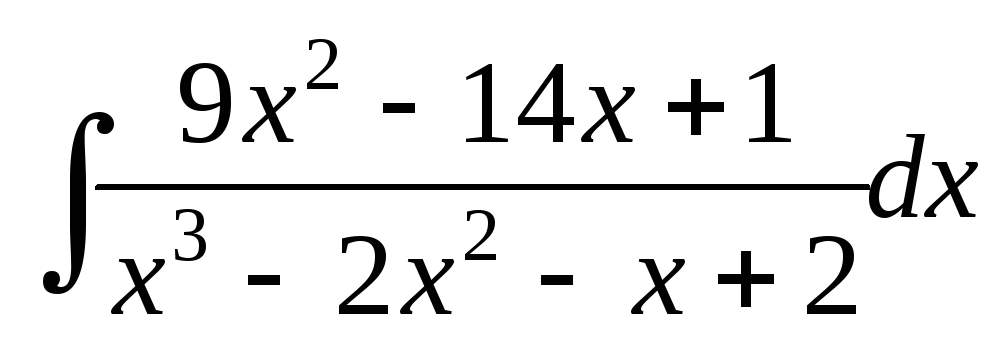 .
.
Тема 3. Интегрирование иррациональных функций
Вопросы для повторения:
Основные методы интегрирования иррациональных функций.
Пример 1. Найти интегралы:
Пусть х = t 2, dx = 2 t∙dt, тогда
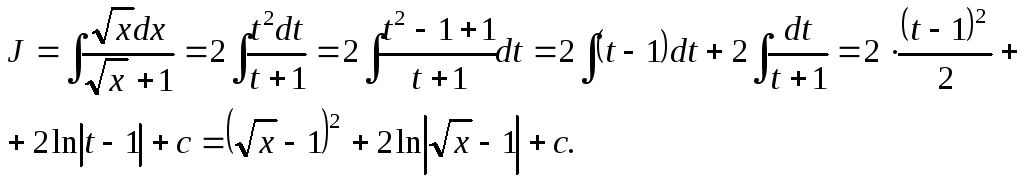
Общий показатель дробных показателей степеней равен 4, поэтому делаем заменух = t 4, dx = 4 t3∙dt. Отсюда
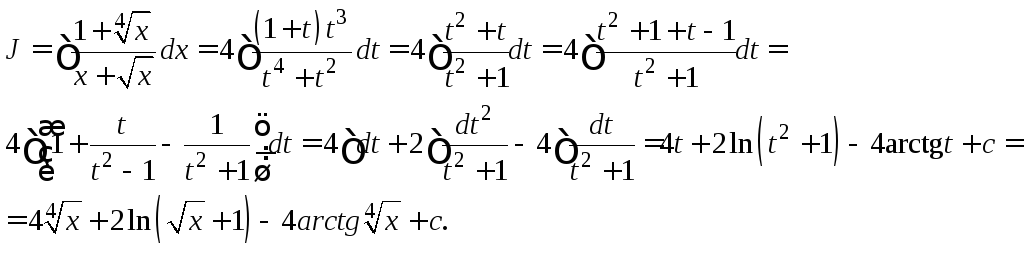
Сделаем замену
![]() ,
,![]() ,
,![]() , получим
, получим
![]()
Представим подынтегральную функцию в виде суммы простейших дробей с неопределенными коэффициентами.
![]() ;
;
![]() ;
;
откуда
![]() ;
;![]() ;
;![]() ;
;![]() .
.
Таким образом,
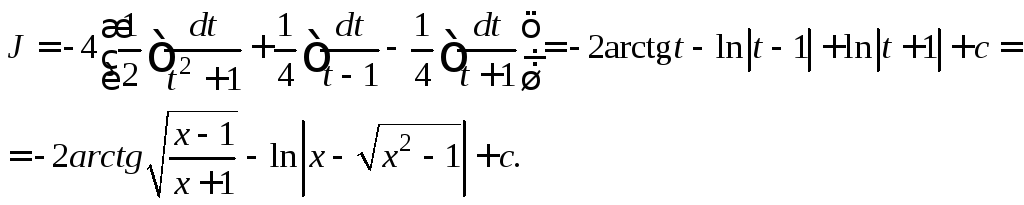
Выделим полный квадрат в подкоренном выражении
![]()
![]()
Выделим под корнем полный квадрат:
![]() и сделаем заменух+ 1 =t,dx=dt,х=t – 1, тогда
получим
и сделаем заменух+ 1 =t,dx=dt,х=t – 1, тогда
получим
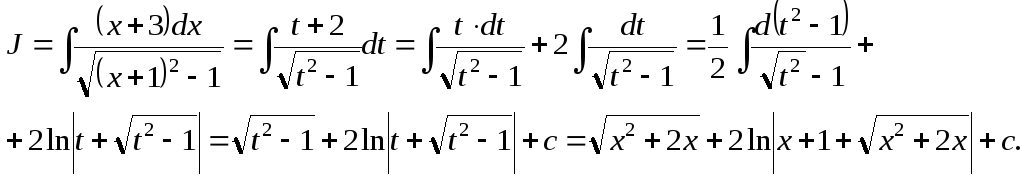
Далее делаем замену
![]() ,
,![]() ,
получим
,
получим
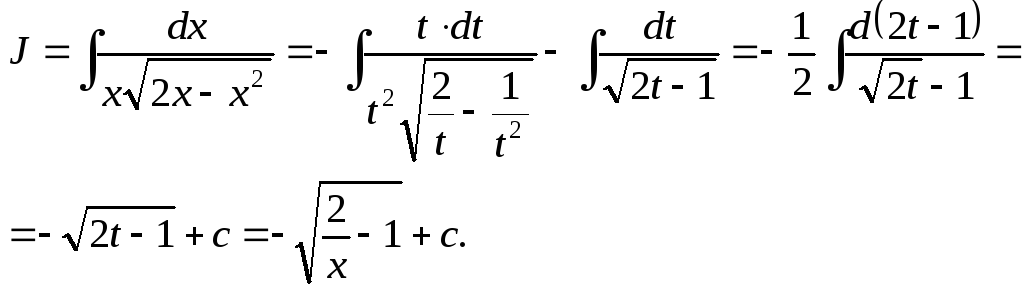
Задачи для самостоятельного решения
Найти интегралы:
 ;
;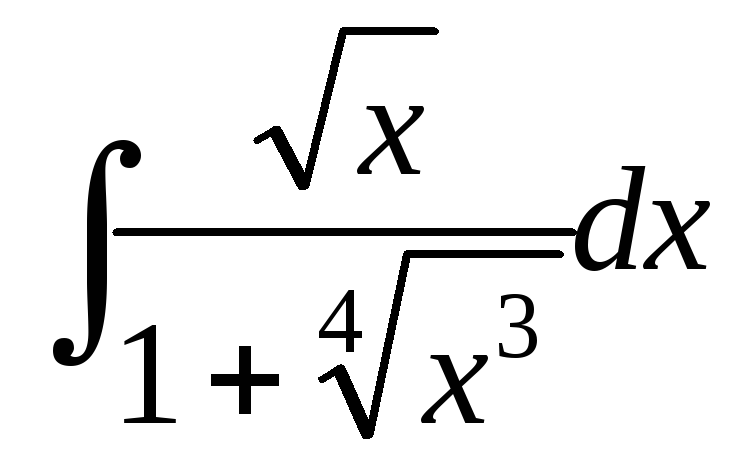 ;
;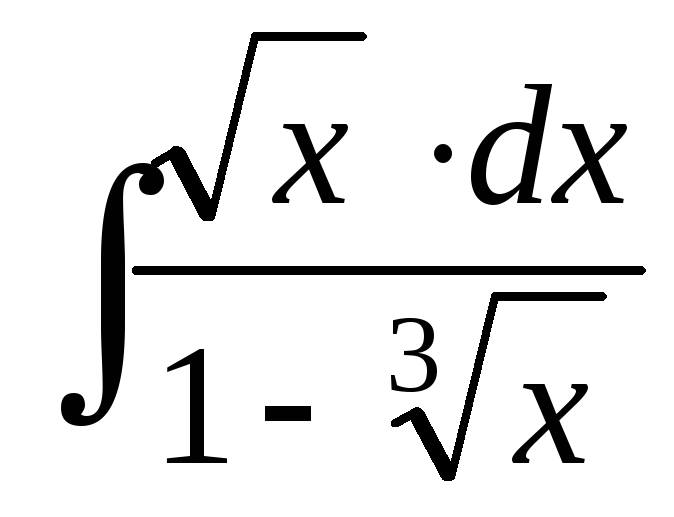 ;
;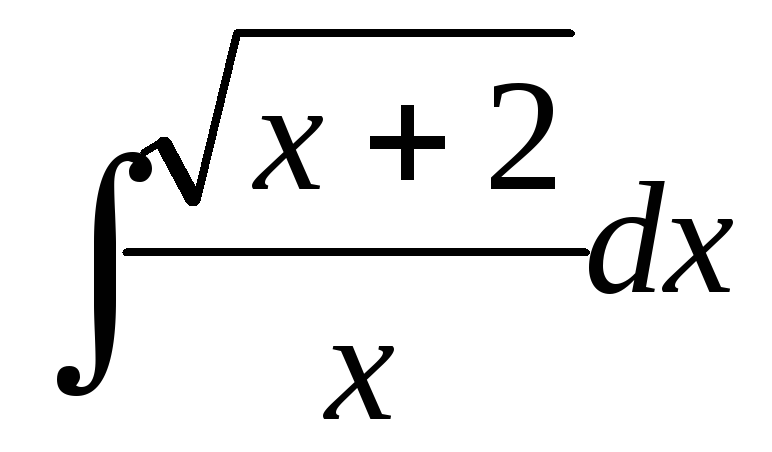 ;
;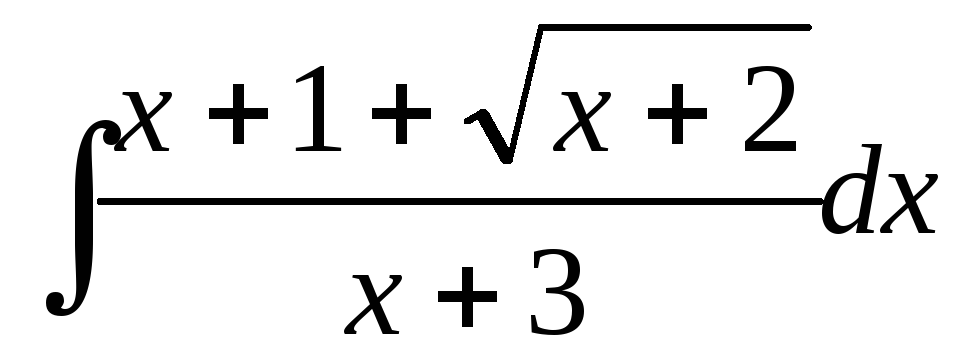 ;
;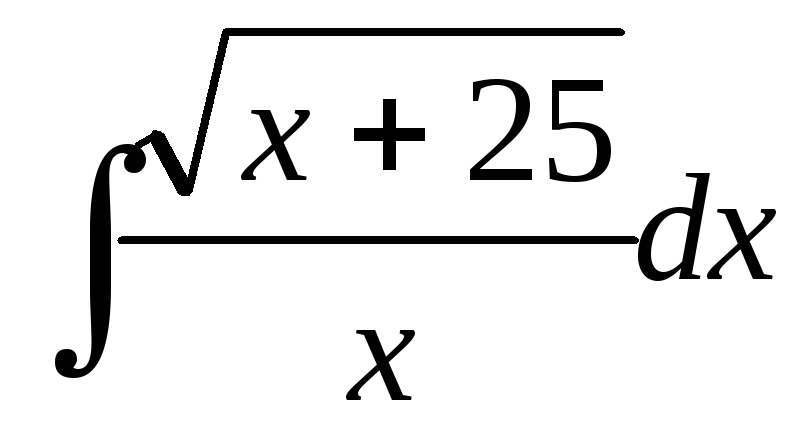 ;
;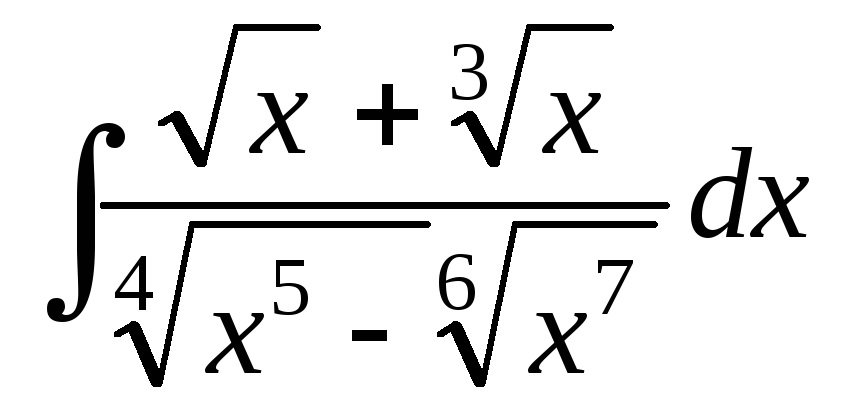 ;
;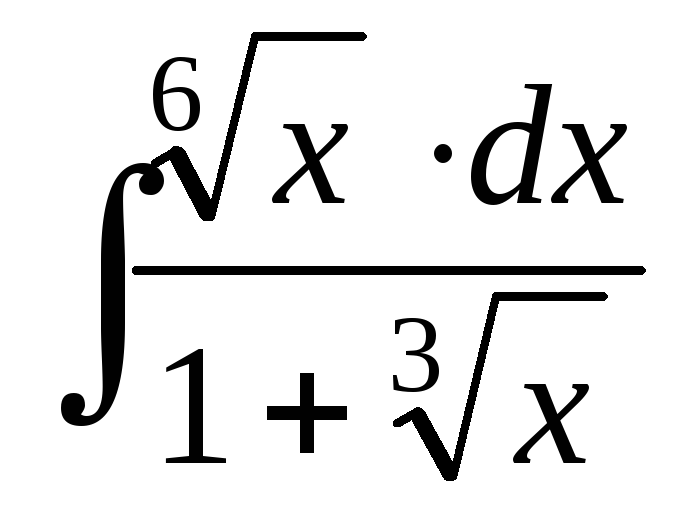 ;
; ;
;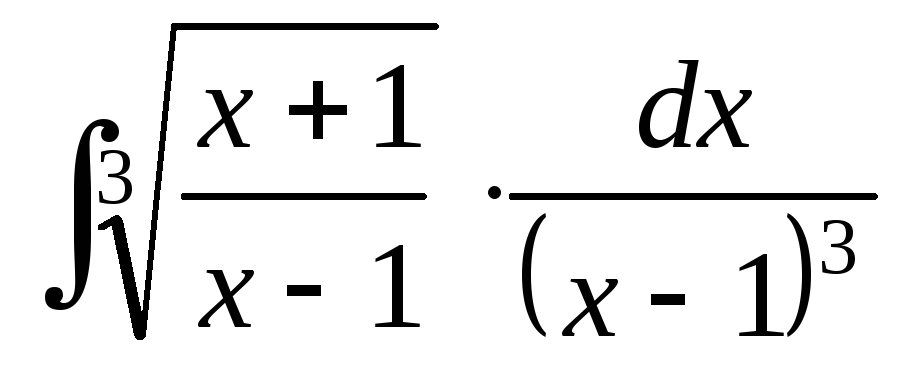 ;
;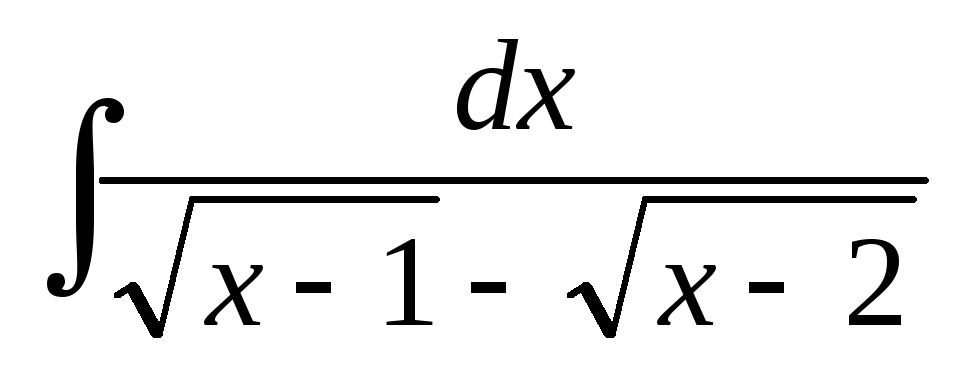 ;
;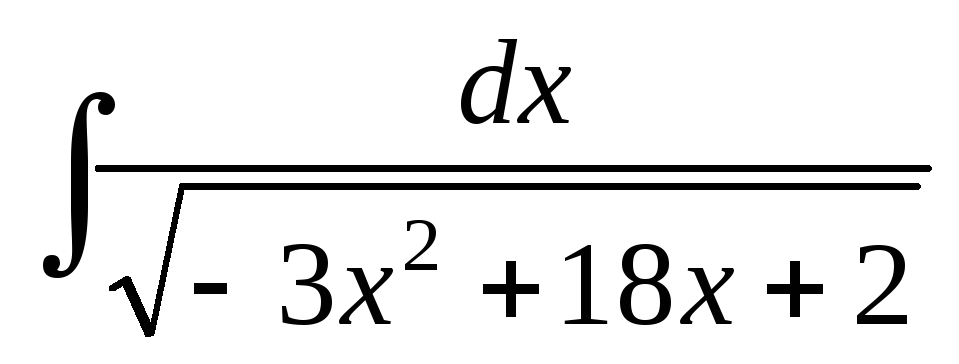 ;
;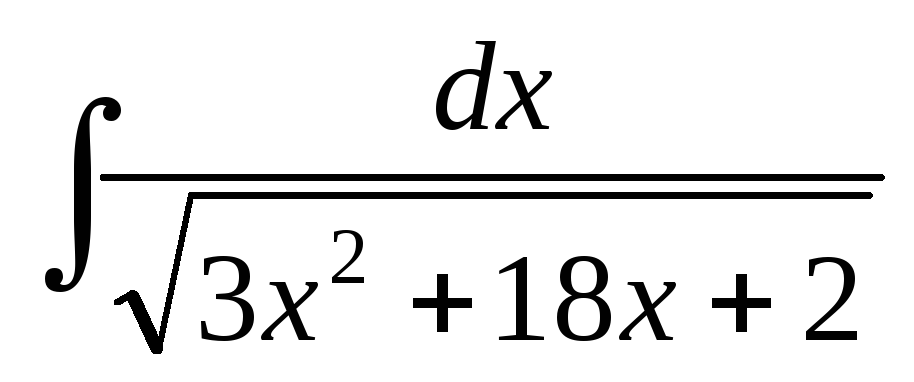 ;
;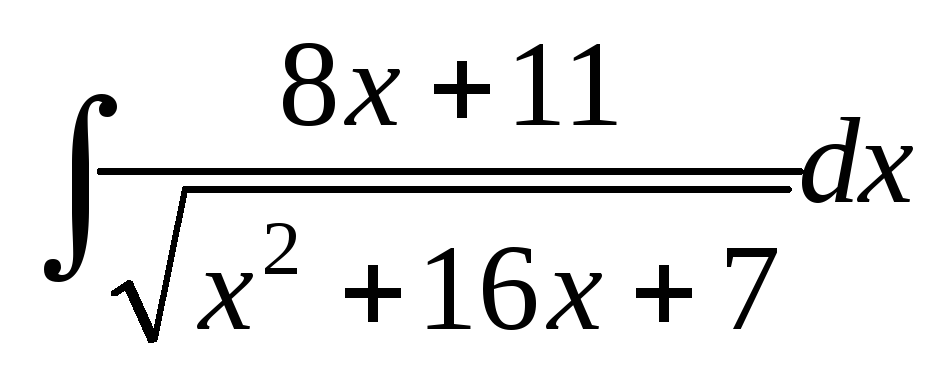 ;
; ;
;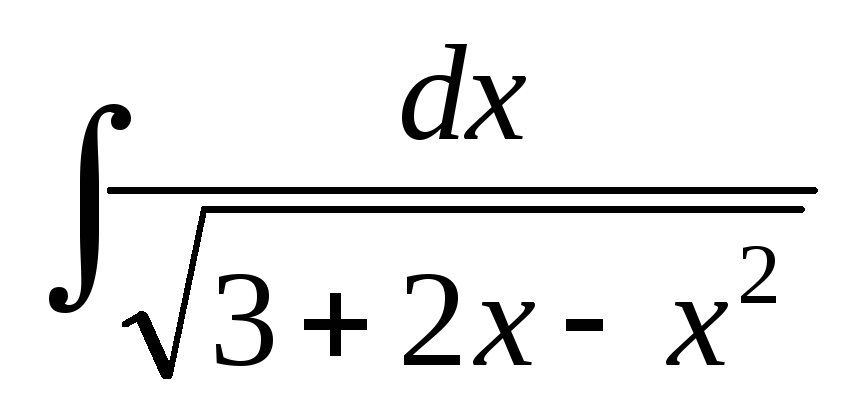 ;
;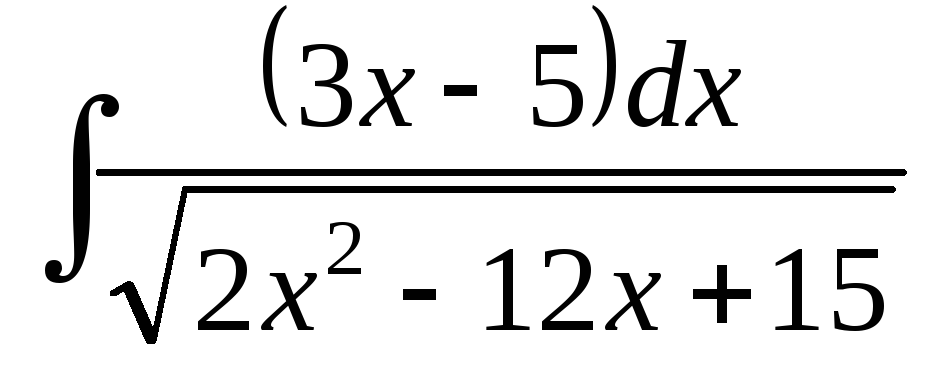 ;
; ;
;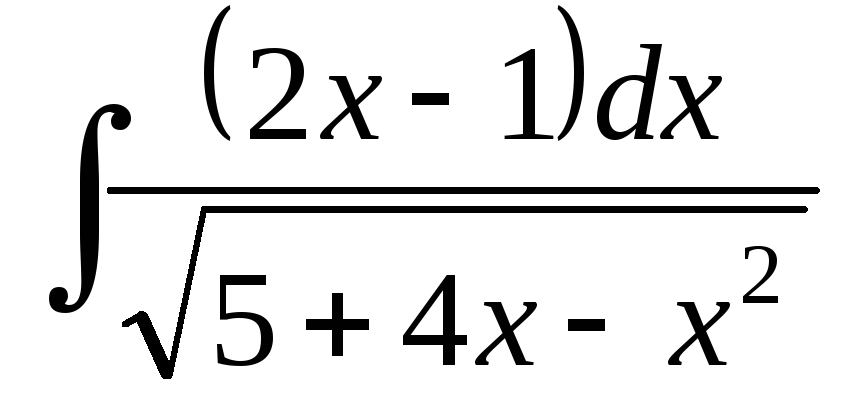 ;
;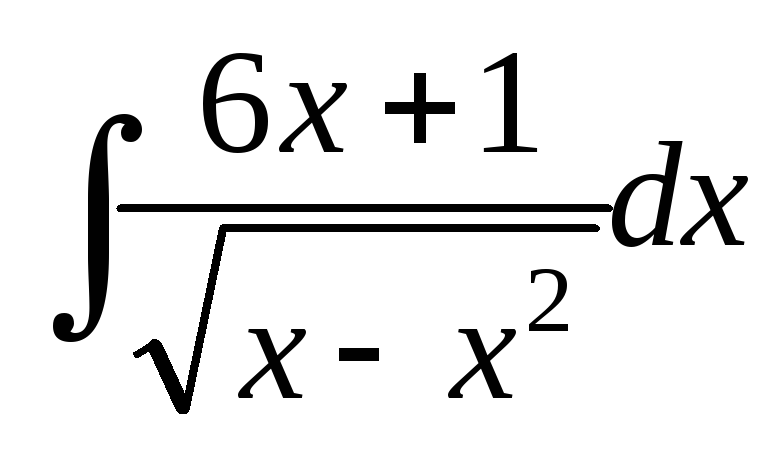 ;
;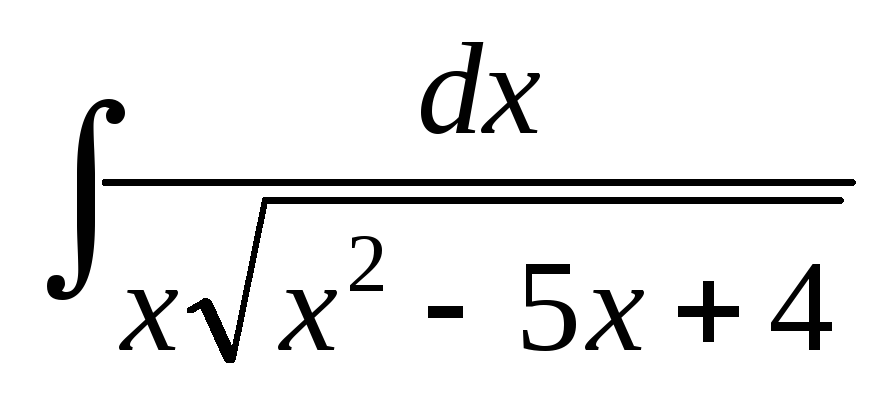 ;
;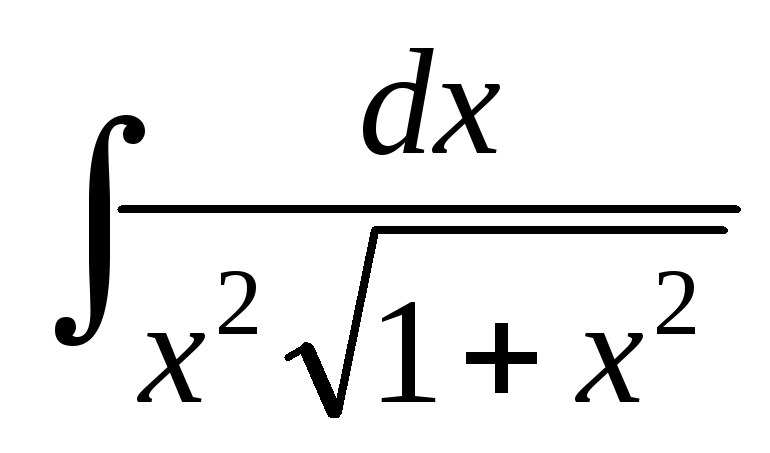 ;
;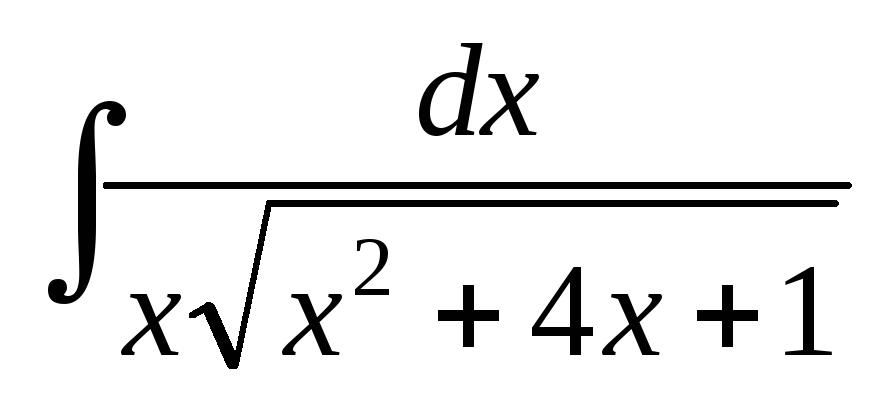 ;
;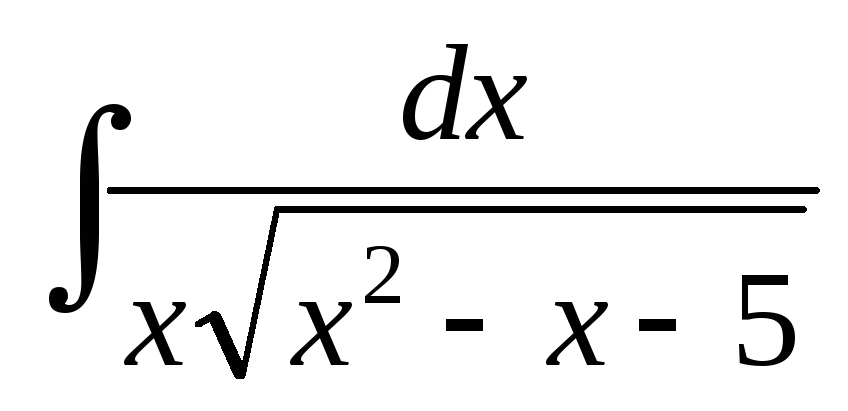 .
.
Тема 4. Интегрирование тригонометрических функций
Вопросы для повторения:
Основные тригонометрические формулы.
Интегрирование функций, содержащих произведения тригонометрических функций.
Интегрирование функций, содержащих произведение степеней синуса и косинуса.
Интегрирование рациональных выражений, содержащих тригонометрические функций.
Пример 1. Найти интегралы:
Преобразуя по формуле
![]() ,
имеем:
,
имеем:
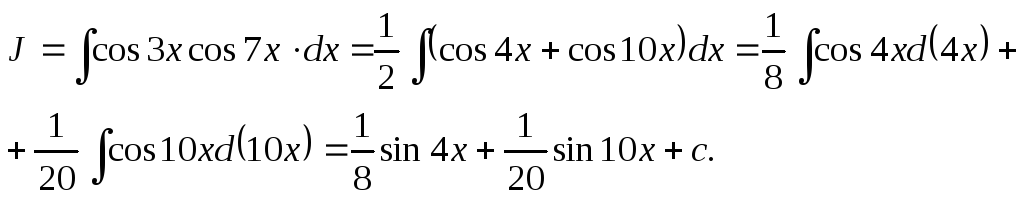
3)
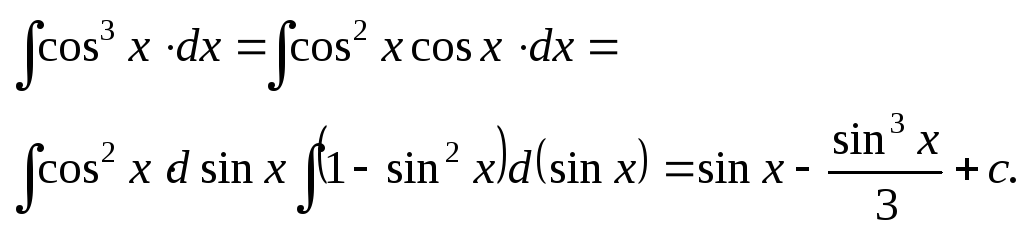
4)
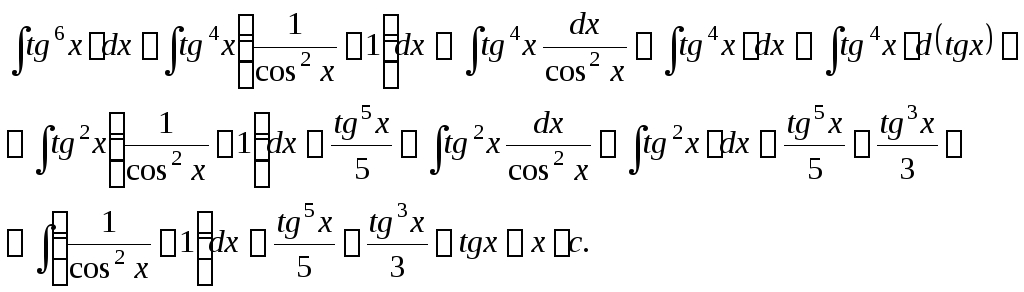
5)
![]()
Пример 2.
Используя формулы понижения порядка
![]() ,
,![]() ,
получим:
,
получим:

Отделяем в числителе от нечетной степени один множитель первой степени и вносим под знак дифференциала:
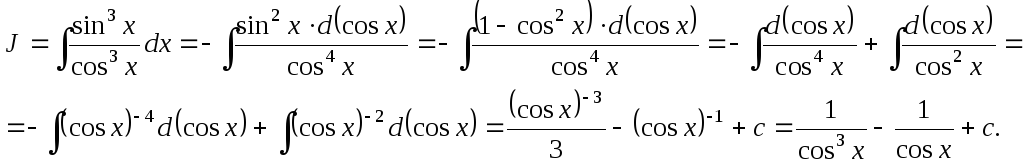
Поскольку синус и косинус в четных
степенях, используем подстановку
![]() ,
,![]() ,
тогда
,
тогда![]() .
.
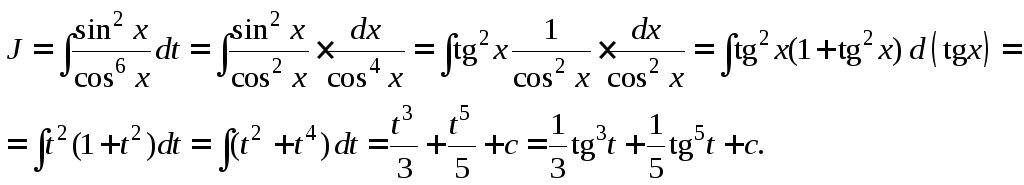
Пример 3.
Используем универсальную тригонометрическую
подстановку
![]() ,
тогда
,
тогда![]() ,
,
![]() ,
,![]() .
.
Получим:
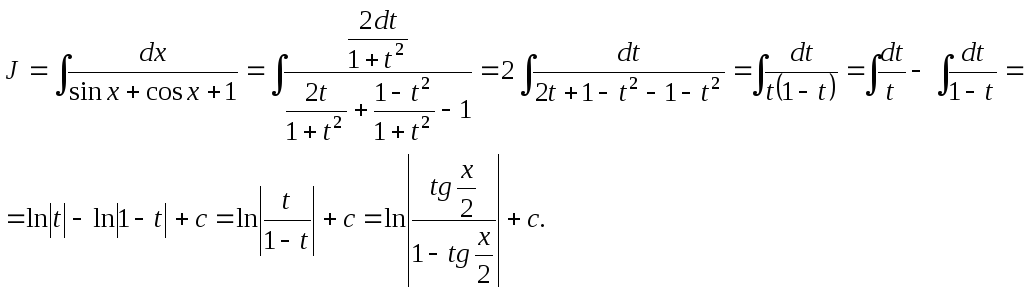
Применим подстановку
![]() ,
тогда
,
тогда
![]() ,
,![]() ,
,![]() ,.
,.
Раздели числитель и знаменатель на cos2x:
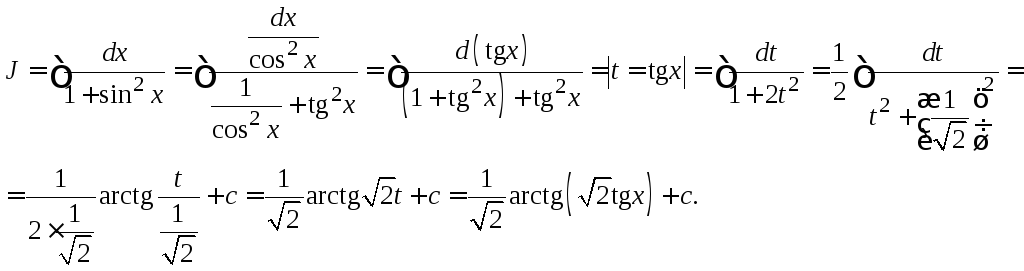
Умножим числитель и знаменатель на cosx, получим
![]()
Задачи для самостоятельного решения
Найти интегралы:
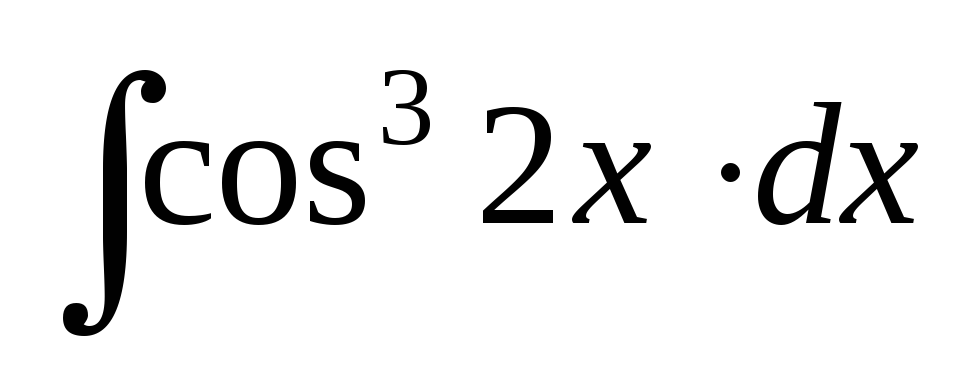 ;
;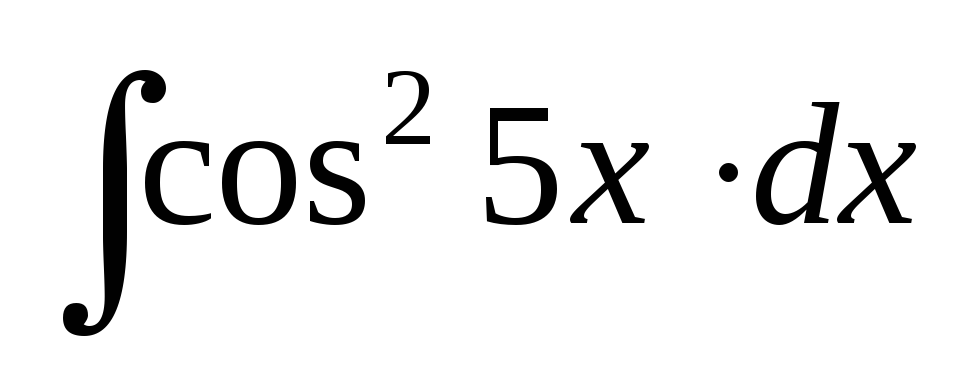 ;
;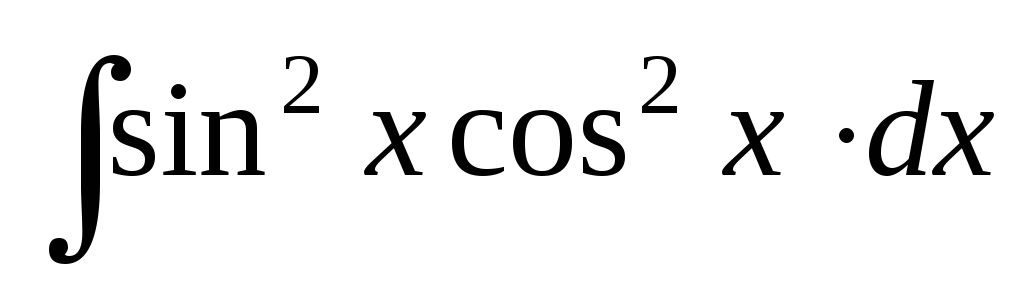 ;
;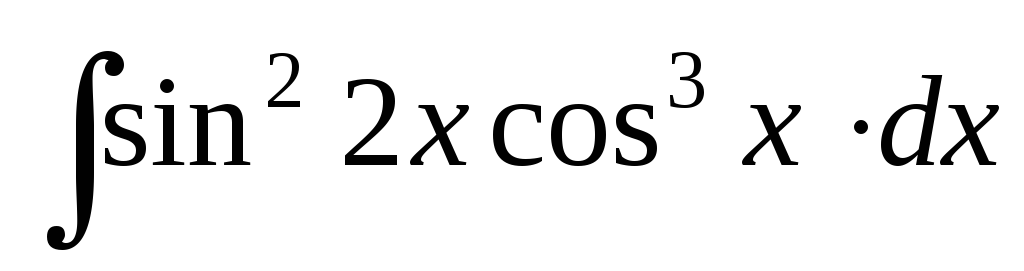 ;
;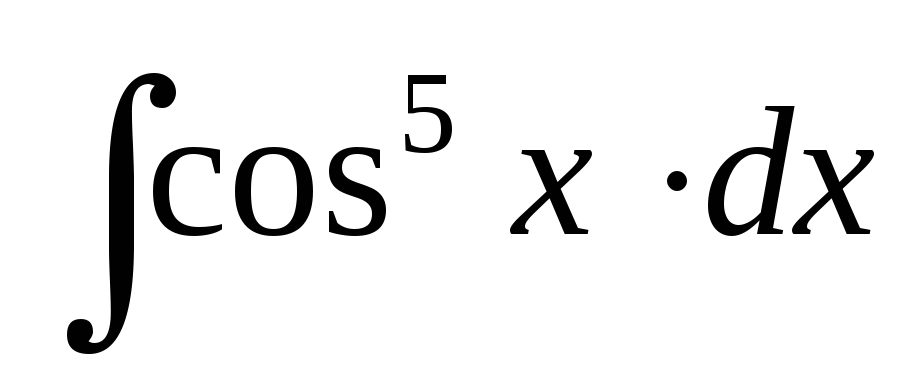 ;
;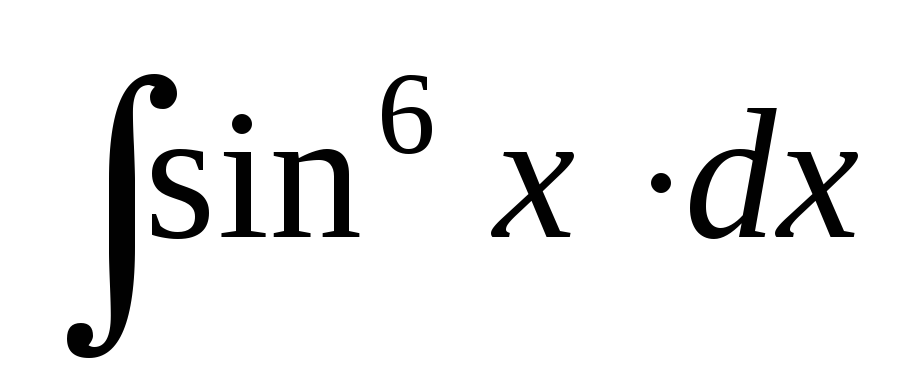 ;
;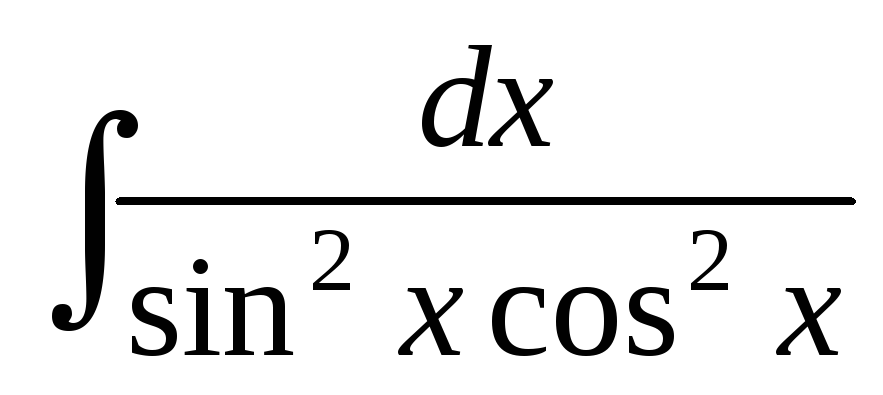 ;
;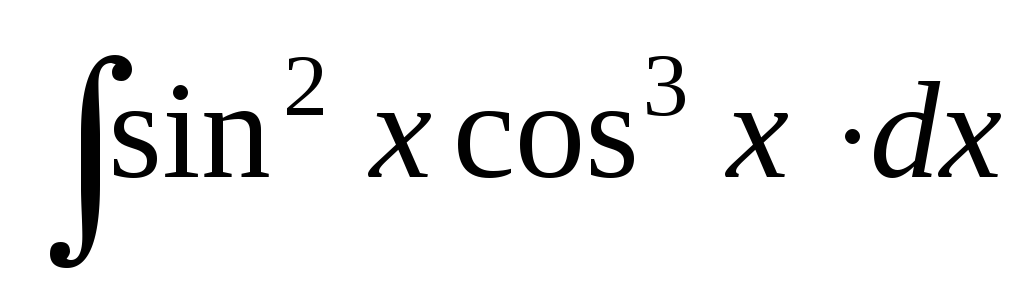 ;
;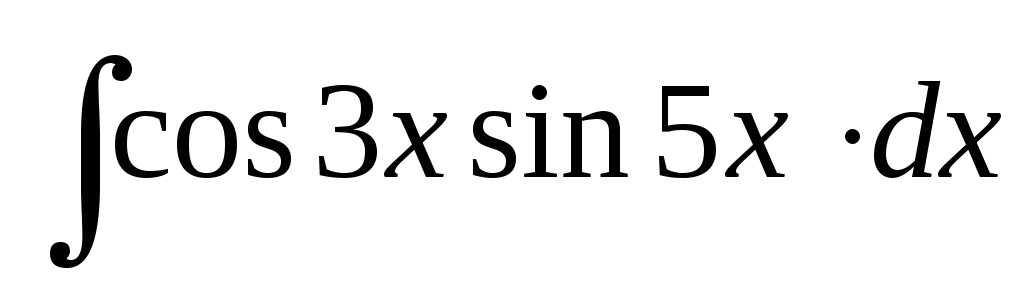 ;
;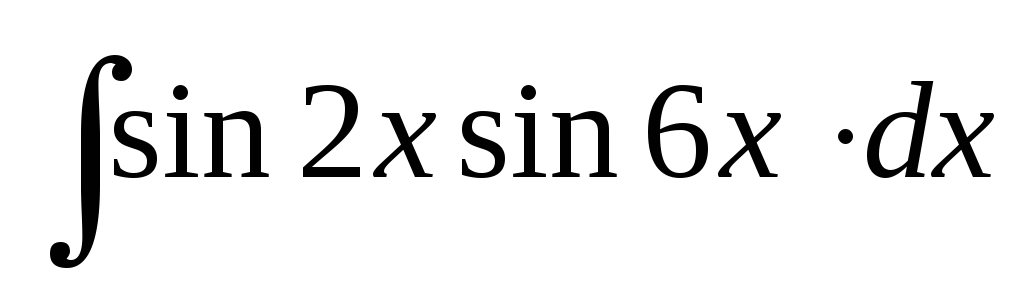 ;
;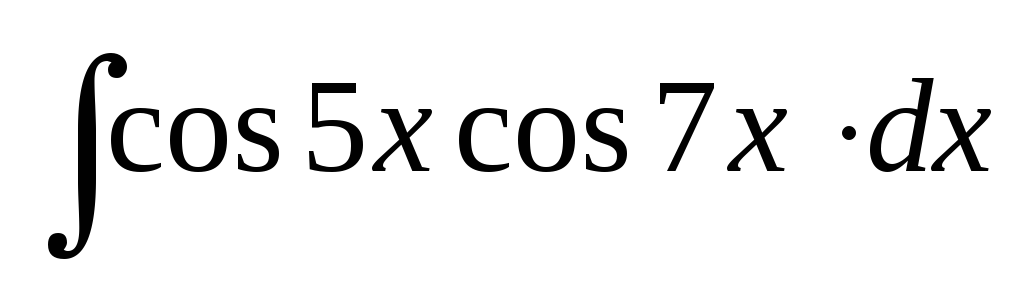 ;
;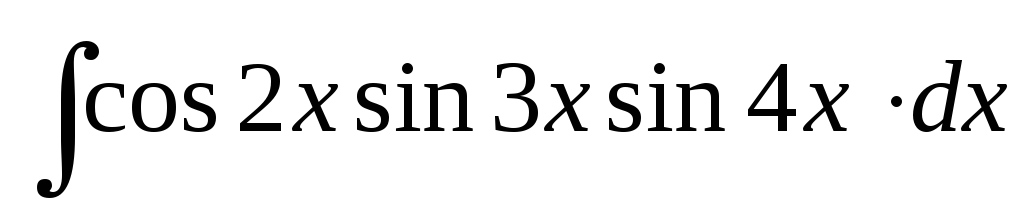 ;
;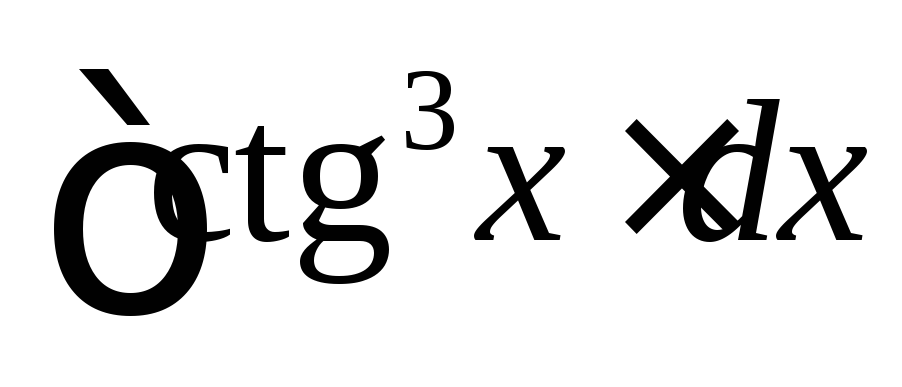 ;
;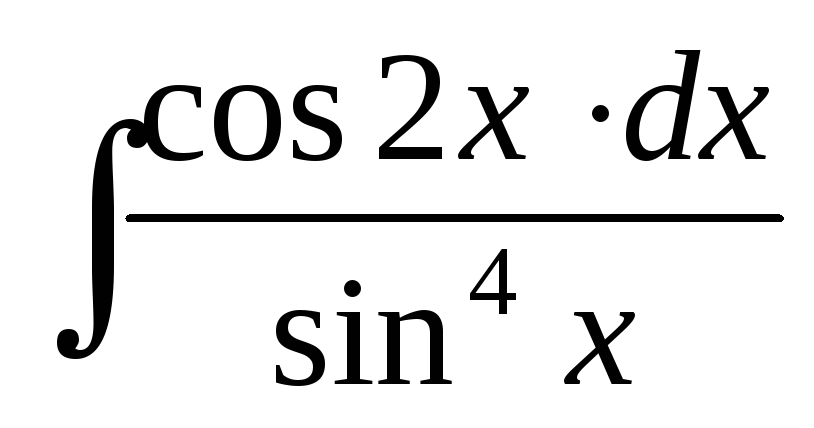 ;
;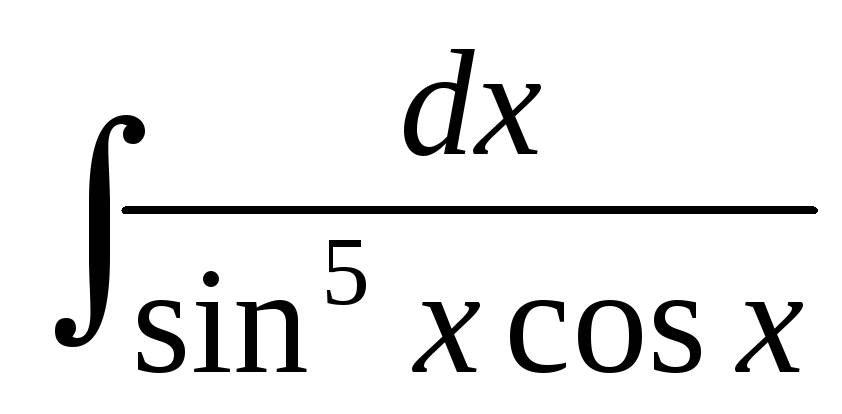 ;
;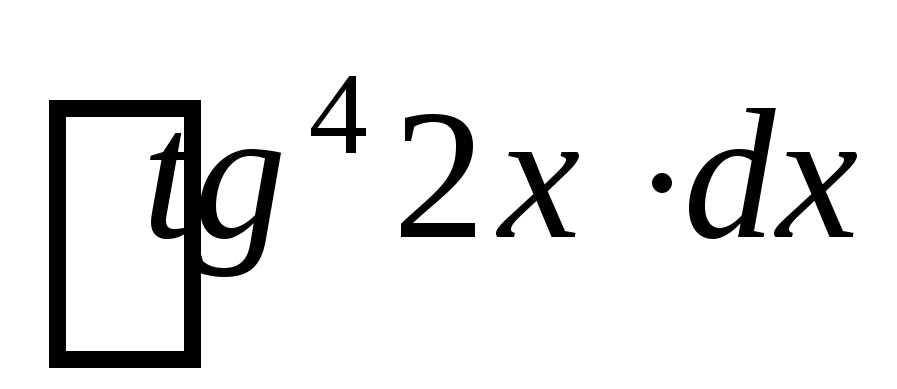 .
.
Найти интегралы:
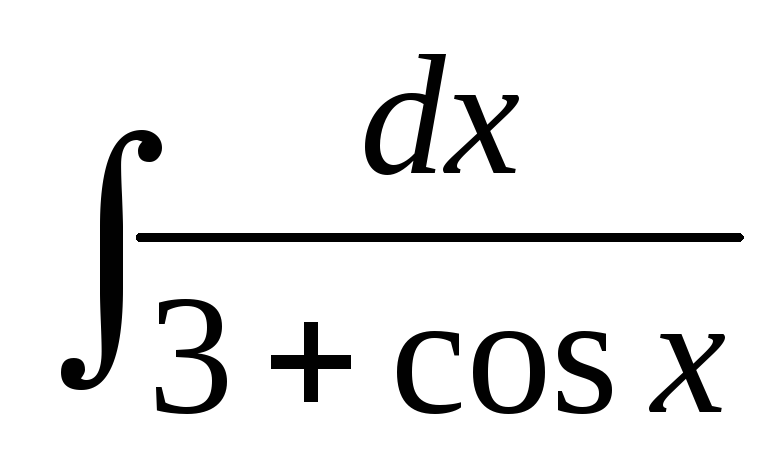 ;
;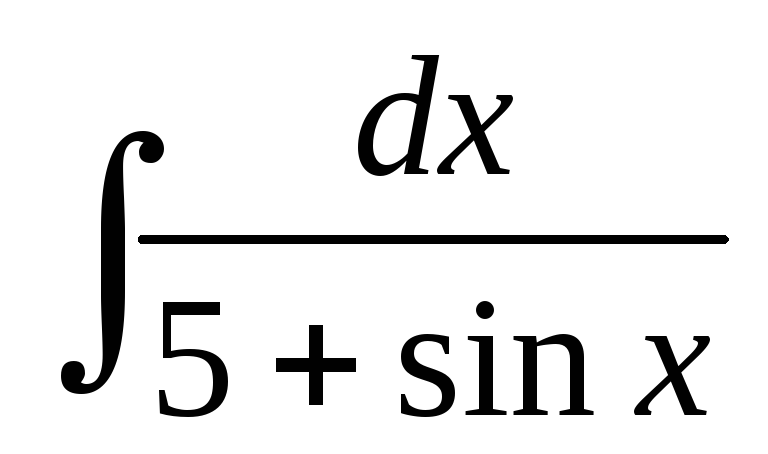 ;
;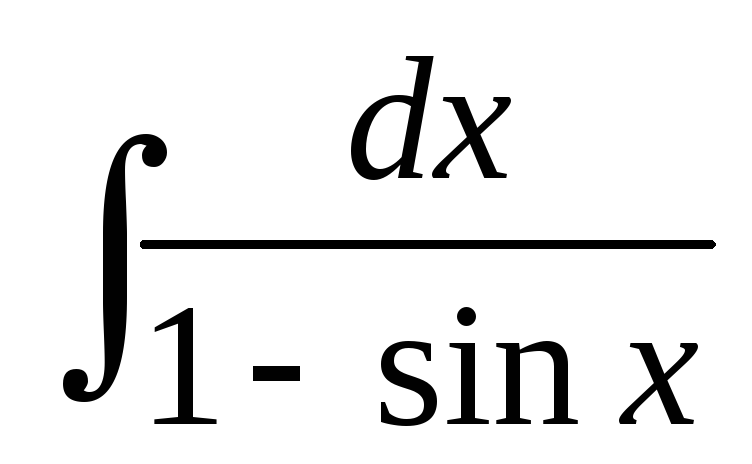 ;
;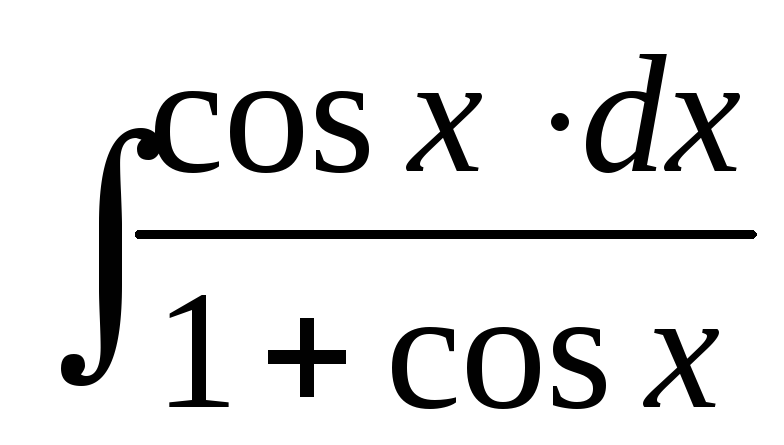 ;
;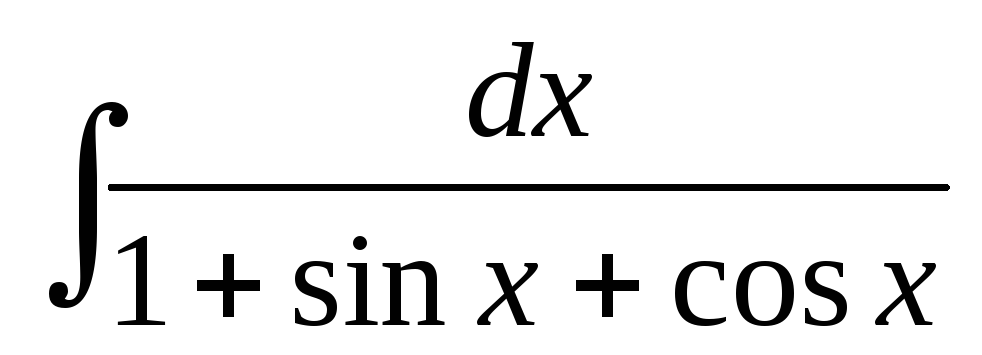 ;
;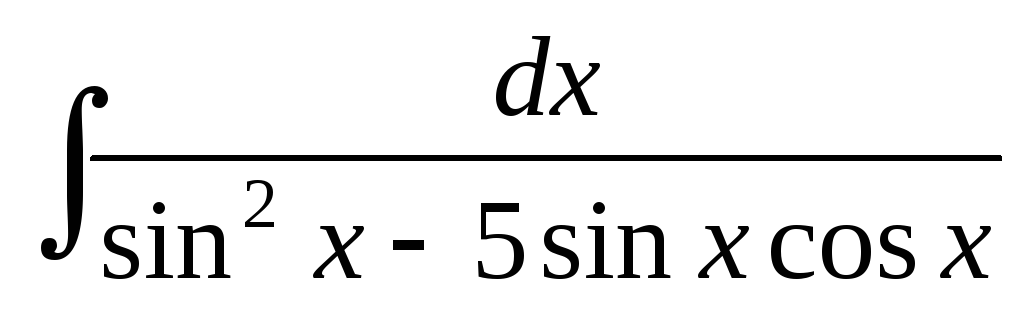 ;
;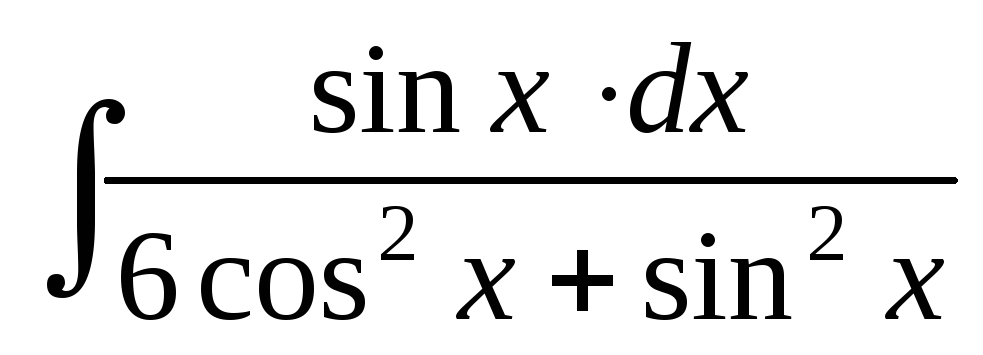 ;
;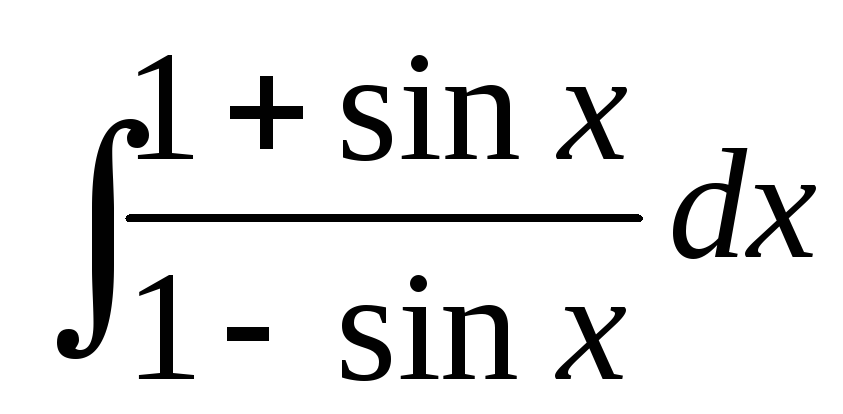 ;
;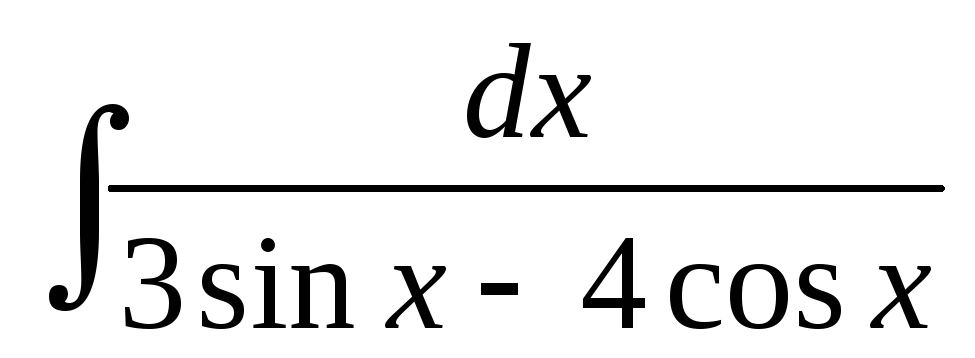 ;
;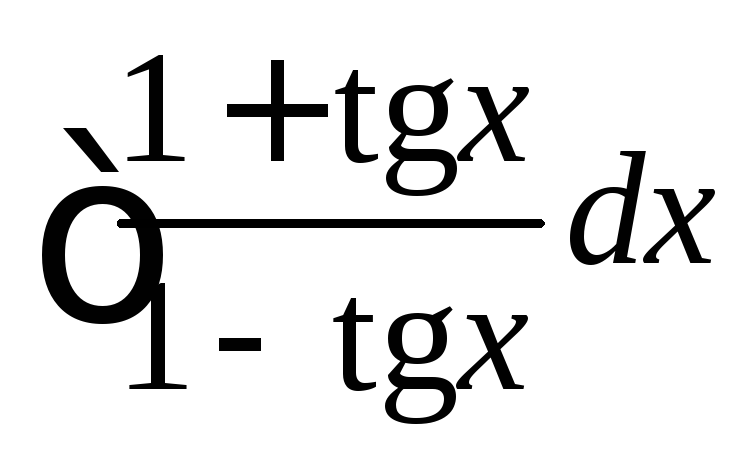 ;
;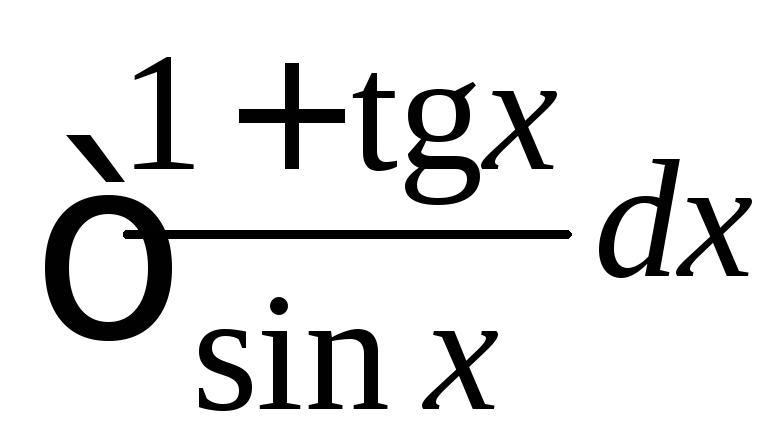 ;
;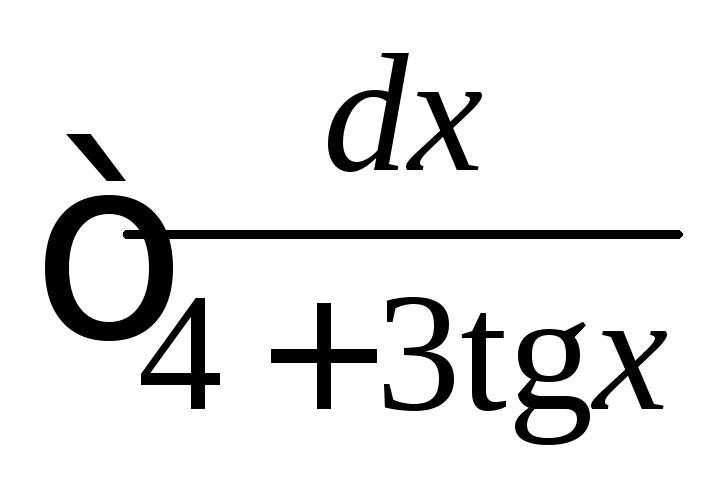 .
.
Тема 5. Определенный интеграл
Вопросы для повторения:
Определенный интеграл и его свойства.
Формула Ньютона-Лейбница.
Метод интегрирования подстановкой.
Метод интегрирования по частям.
Пример 1. Используя формулу Ньютона-Лейбница вычислить интегралы:
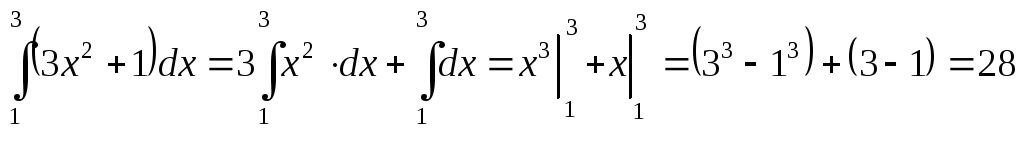 ;
; ;
; ;
;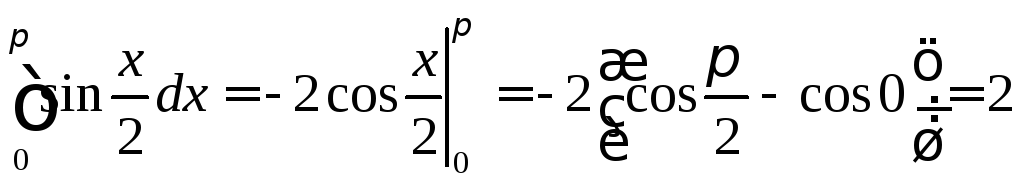 .
.
Пример 2. Вычислить определенные интегралы методом замены переменной:
Сделаем замену переменной х=t2, тогдаdx= 2t∙ dt.Находим новые пределы интегрирования: еслих= 0, тоt =0; еслих= 3, тоt =√3.
Тогда
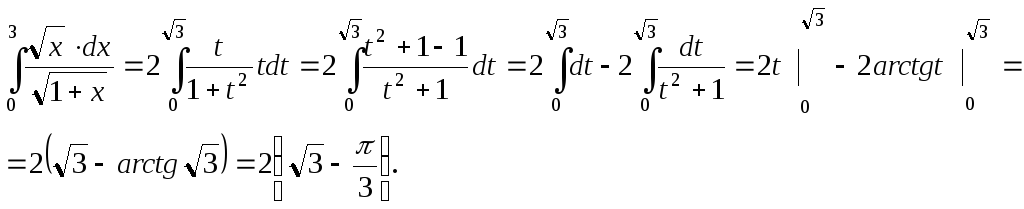
Пусть ех=t,
тогдах=lnt,![]() .
Находим новые пределы интегрирования:
еслих=ln2,
то t
=2;прих=ln3t
=3.
.
Находим новые пределы интегрирования:
еслих=ln2,
то t
=2;прих=ln3t
=3.
Отсюда
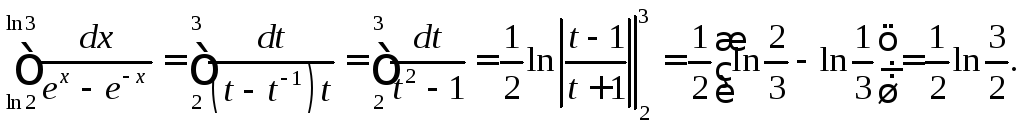
Так как cosx∙dx=d(sinx), то сделаем заменуsinx = t.Определим новые пределы интегрирования: прих= 0,t =0; еслих= π/2, тоt =1.
Следовательно,
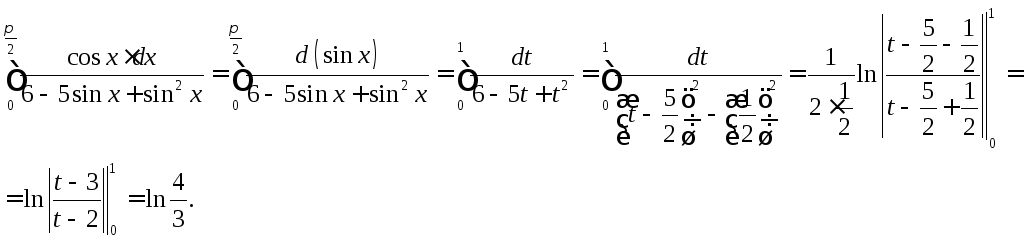
Пример 1. Используя формулу интегрирования по частям для определенного интеграла, вычислить интегралы: