1.5. Задача про призначення

Назва задачі – про призначення – походить з практичної кадрової ситуації, коли претендентів треба призначити на вакантні посади найкращим чином.

Модель цієї задачі має широке застосування при розподілі неділимих ресурсів – машин, будівель, контейнерів, транспортних засобів, в тому числі, людей.

Постановка задачі. Маємо видів робіт, кожна з яких виконується тільки одним зспособів (), причому кожен спосіб можна використати тільки для одного виду роботи. Відома оцінка ефективностівиконанняi-го виду роботи j-м способом . Необхідно знайти такий план виконання робіт, щоб сумарна ефективність була максимальною.

Нехай шукана змінна приймає одне з двох значень: 1 (якщоi-й вид роботи виконується j-м способом) або 0 (якщо i-й вид роботи не виконується j-м способом), тобто . Тоді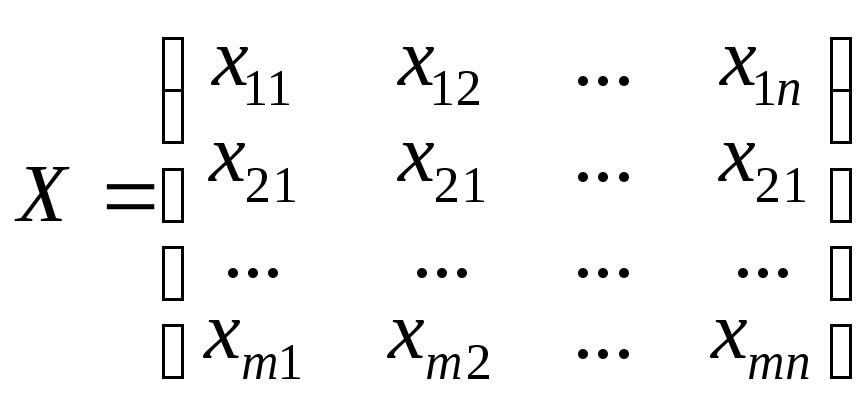– план виконання робіт, – сумарна ефективність.

Відповідно до постановки задачі, математична модель має вигляд:

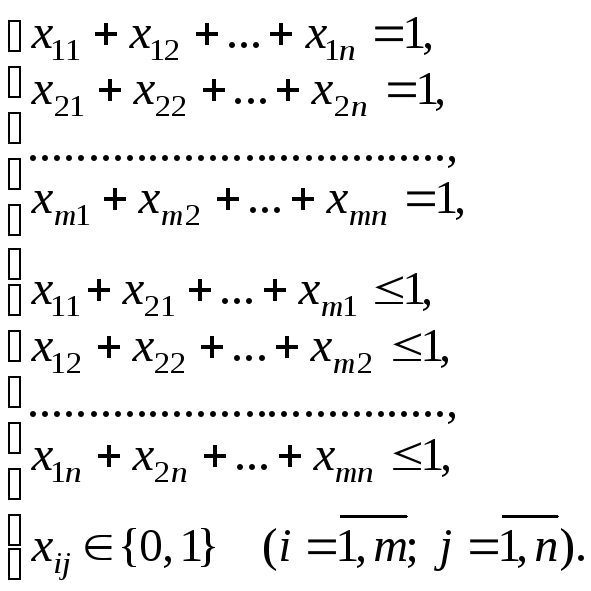
Загальна постановка задач лінійного програмування (лп)

Дано систему обмежень у виді системи лінійних рівнянь та нерівностей

.

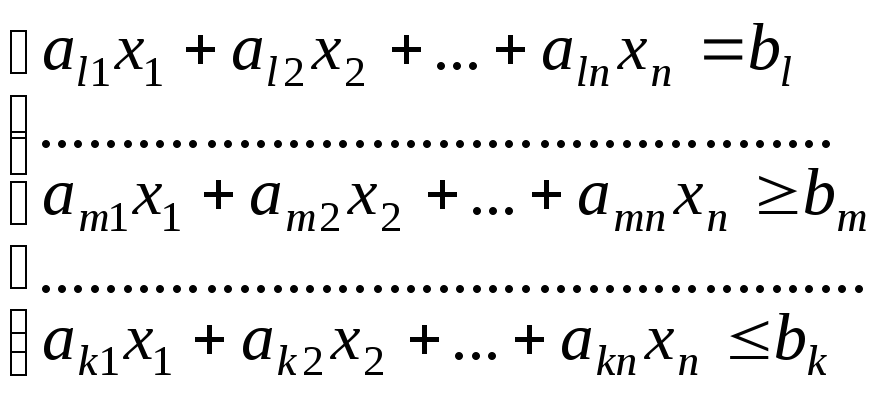Знайти такий план (рішення системи) , при якому лінійнафункція мети f набуває оптимального (максимального або мінімального) значення

.

Перелік питань для самоперевірки

1. Економіко-математична модель.

2. Побудова математичних моделей економічних задач (приклади задач лінійного програмування).

3. Задача планування виробництва.

4. Задача складання раціону.

5. Транспортна задача.

6. Задача про мінімізацію відходів.

7. Задача про призначення.

8. Загальна задача лінійного програмування (ЛП).

Лекція 2

Тема 2. Геометрична інтерпретація задач лінійного програмування. Задача лінійного програмування, форми її запису

Геометричний метод розв’язання задач ЛП

Геометричний метод дозволяє розв’язувати задачі ЛП, система обмежень яких має вигляд системи нерівностей з двома змінними.

Схема розв’язання задачі ЛП геометричним методом:

1. Знаходимо і зображуємо на площині область допустимих рішень (ОДР) – множину точок, координати яких задовольняють системі обмежень. Якщо ця область – порожня, то задача не має розв’язку. Якщо ця область – опуклий многокутник, то задача завжди має розв’язок. У випадку необмеженої області задача може мати, а може й не мати розв’язок.

2. Серед точок ОДР знаходимо таку, в якій функція мети набуває оптимального значення. Для цього:

а) Зображуємо градієнт функції мети – вектор з початком у точці О(0;0) і кінцем – у точці з координатами, що дорівнюють коефіцієнтам при відповідних змінних цієї функції. Зображуємо лінію рівня функції мети f – пряму, уздовж якої ця функція набуває одного й того ж фіксованого значення a, тобто (лінія рівня завжди перпендикулярна градієнту). Важливою властивістю лінії рівня є те, що при її паралельному зміщенні в напрямку градієнта значення функції мети зростає, а при зміщенні в протилежному напрямку – спадає.

б) переміщуємо лінію рівня паралельно самій собі у напрямку градієнта при (у напрямку, протилежному градієнту, при) до крайнього її положення на ОДР. Точка ОДР, через яку проходить лінія рівня у своєму крайньому положенні, є точкою максимуму (мінімуму) функції мети. Якщо при переміщенні лінії рівня неможливо досягти відповідного крайнього положення, то задача не має розв’язку.

Зауваження 2.1. Задача має єдиний оптимальний розв’язок, коли лінія рівня у своєму крайньому положенні проходить тільки через одну кутову точку многокутника розв’язків системи обмежень. Якщо лінія рівня у своєму крайньому положенні збігається з гранню многокутника (наприклад, з відрізком АВ), задача має нескінченно багато оптимальних розв’язків (їх задають координати точок відрізка АВ: ).

Задача 2.1. Розв'язати задачу лінійного програмування геометричним методом.

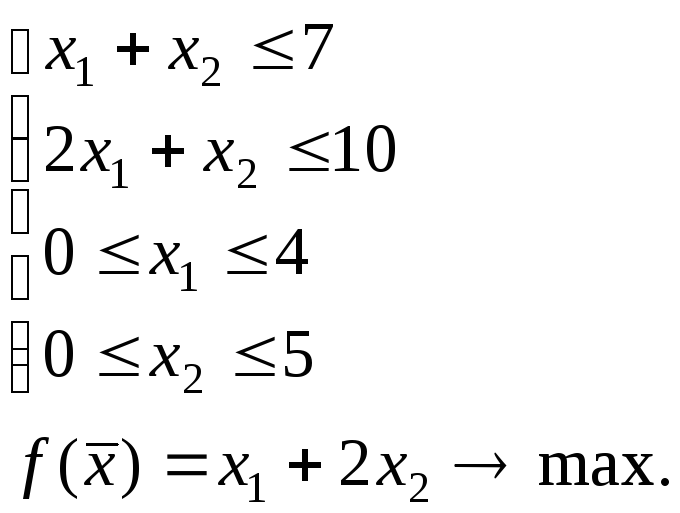
Рішення

Знаходимо і зображуємо на площині ОДР. Будуємо пряму (I) , що відповідає першій нерів-ності, по точках: (0;7) і (7;0). Геометричним розв’язком даної нерівності є напівплощина, що містить точку (0;0), оскільки координати точки (0;0) задовольняють нерівності . Ця напівплощина позначена на рисунку стрілкою, перпендикулярною до прямої (I).

Аналогічно, побудуємо прямі

та зобразимо напівплощини, відповідні нерівностям системи обмежень.

Перетин побудованих напівплощин дає ОДР – шестикутник OABCDE.

2. Зображуємо градієнт функції мети: gradf=(1;2). Зображуємо лінію рівня функції мети x₁+2x₂=0, що проходить через початок координат перпендикулярно градієнту.

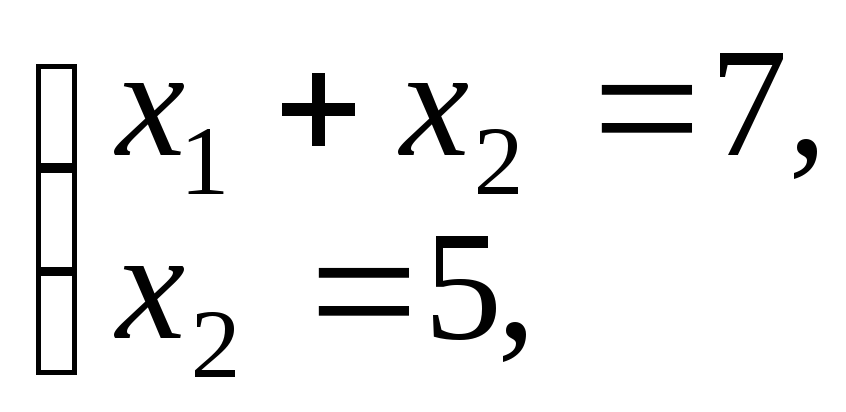Пересуваючи лінію рівня в напрямку градієнта (у напрямку зростання функції мети), знайдемо точку В, у якій функція f має максимальне значення. Оскільки точка В знаходиться на перетині прямих (I) і (IV), її координати визначаються розв’язанням системи рівнянь цих прямих тобто x₁ = 2, x₂ = 5; B =(2;5).

Максимальне значення функції мети:

Відповідь: