Перелік питань для самоперевірки

1. Економічна і математична постановка транспортної задачі. Умова існування її розв’язку.

2. Приведення транспортної задачі до замкненої форми.

3. Методи побудови опорного плану.

4. Пошук оптимального плану перевезень за методом потенціалів.

Змістовий модуль 3

Задачі цілочислового програмування.

Задачі теорії ігор

Тема 6. Цілочислове програмування

При розв’язанні багатьох задач нецілочислове рішення не має сенсу. Розділ математичного програмування, в якому на екстремальні задачі накладено умову дискретності змінних при скінченній області допустимих рішень, зветься дискретним програмуванням. За наявності умови цілочисловості йдеться про підрозділ дискретного програмування – цілочислове програмування.

В економіці є багато задач з фізичною неподільністю об’єктів, предметів і факторів розрахунку. Наприклад, не можна збудувати 1.7 будівлі, 6.1 заводів, 1.07 автомобіля, здійснити 3.4 подорожі, купити 4.5 туристичних путівок.

Розглянемо модель цілочислового програмування.

Необхідно оптимізувати

(6.1)

за обмежень:

		(6.2)
		(6.3)

Обмеження (6.2), якщо задача лінійного програмування має розв’язок, визначає опуклу область допустимих рішень, наприклад, область OABCD (рис. 6.1).

Вузли цілочисельної гратки є допустимими рішеннями задачі цілочислового програмування. Область OA’B’C’D’ є такою, до якої належать усі допустимі рішення задачі (6.1) – (6.3) (див. рис. 6.1).

Розв’язання задачі цілочислового програмування здійснюється шляхом побудови і розв’язання розширеної задачі лінійного програмування, яка доповнюється лінійними обмеженнями, котрі випливають з умов вихідної цілочислової задачі.

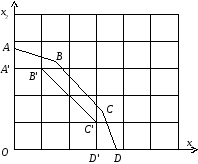
Рис. 6.1

6.1. Метод відсікань Гоморі

Ідея методу відсікань полягає в наступному. Спочатку розглядаємо опуклу множину, яка визначається лінійними обмеженнями за умов невід’ємності змінних вихідної задачі лінійного програмування. Відшукуємо екстремальну точку цієї множини. Якщо здобуте рішення нецілочислове, то треба ввести додаткове обмеження, котре відсікає частину області допустимих рішень вихідної задачі лінійного програмування разом зі здобутим нецілочисловим оптимальним рішенням. При цьому в частині, що відсікається, не має бути жодної цілочислової точки.

Потім розглядаємо розв’язок вихідної задачі лінійного програмування з урахуванням нового обмеження. Якщо воно нецілочислове, то треба ввести нове обмеження і так доти, поки не буде знайдене цілочислове оптимальне рішення.

Алгоритм методу відсікань полягає в наступному.

Крок 1. Відшукати симплексним методом оптимальне рішення задачі лінійного програмування з цільовою функцією (6.1) та лінійними обмеженнями (6.2) без урахування умови цілочисловості (6.3). Нехай воно має вид: . Якщо це оптимальне рішення цілочислове– обчислення припиняються. В противному разі треба перейти до кроку 2.

Крок 2. Обрати дробову компоненту оптимального рішення. Її вибір є достатньо довільним, але для підвищення збіжності обирається компонента з більшою дробовою частиною.

Нехай такою компонентою буде , тодіk-й рядок симплекс-таблиці звуть індексним. Рівняння цього рядка:

або

,

(6.4)

де – базисна змінна,– небазисні (вільні) змінні відповідного оптимального рішення.

Записати нерівність відсікання Гоморі:

,

(6.5)

де фігурні дужки означають дробову частину числа.

До лівої частини нерівності (6.5) додати додаткову невід’ємну змінну і записати таке рівняння

.

(6.6)

Ввести рівняння (6.6) в систему обмежень (6.2).

Крок 3. Отриману розширену задачу розв’язати симплексним методом. Якщо оптимальне рішення цієї задачі цілочислове – обчислення припиняються. В противному випадку необхідно повернутися до кроку 2 алгоритму.

Теоретично доведено, що даний алгоритм збігається до оптимуму за скінченну кількість ітерацій. Алгоритм не гарантує одержання цілочислового рішення до самої останньої ітерації.

Якщо в процесі рішення з’явиться рівняння (6.4) з нецілим вільним членом і цілими іншими коефіцієнтами, то дана задача не має цілочислового оптимального рішення.

Зауваження 6.1. Цілою частиною числа a називається найбільше ціле число [a], що не перевищує a, а дробовою частиною числа a – число {a}, яке дорівнює різниці між цим числом і його цілою частиною, тобто .

Наприклад,

1) , ,;

2) ,,.

Задача 6.1. Для придбання обладнання для сортування зерна фермер виділяє 34 грош. од. Обладнання має бути розташовано на площі, що не перевищує 60 кв. м. Фермер може замовити обладнання двох видів: машини типу А вартістю 3 грош. од., що потребують площу 3 кв. м і забезпечують продуктивність за зміну 2 т зерна, і машини типу B вартістю 4 грош. од., що потребують площу 5 кв. м і забезпечують продуктивність за зміну 3 т зерна.

Потрібно скласти оптимальний план придбання обладнання, яке б забезпечило максимальну загальну продуктивність.

Рішення

1. Побудуємо математичну модель задачі.

Позначимо через кількість машин типуА і B відповідно, через f – загальну продуктивність.

Тоді математична модель задачі матиме вид:

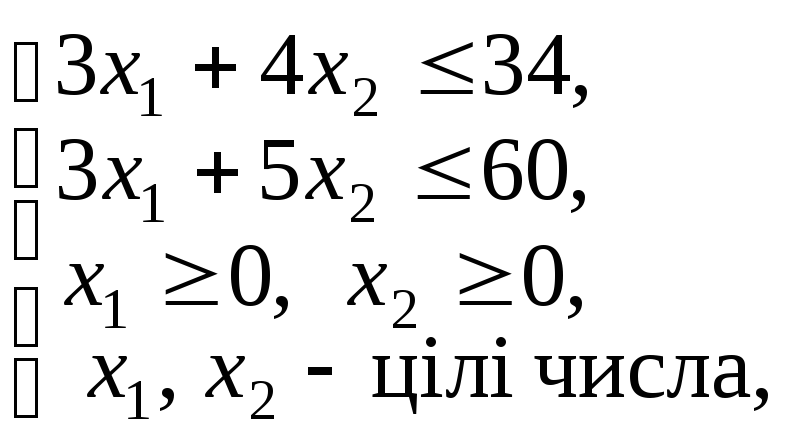
2. Симплексним методом розв’язуємо цю задачу без урахування умови цілочисловості.

Одержуємо оптимальне рішення: . Цьому рішенню відповідає наступна симплекс-таблиця.

Таблиця 6.1
Б	сБ	b	x1	x2	x3	x4
			–2	–3	0	0
x2	–3	17/2	3/4	1	1/4	0
x4	0	35/2	–3/4	0	–5/4	1
		–51/2	–1/4	0	–3/4	0

Рішення не задовольняє умові цілочисловості, тому що має дробові компоненти: 17/2, 35/2.

3. Компоненти 17/2, 35/2 мають однакові дробові частини, які дорівнюють 1/2. Тому обираємо одну з цих компонент, наприклад 17/2.

Рівняння відповідного рядка симплекс-таблиці (табл. 6.1):

,

де – базисна змінна,,– небазисні (вільні) змінні.

Виражаємо базисну змінну через небазисні змінні:

.

Записуємо нерівність відсікання Гоморі:

.

Знаходимо дробові частини чисел:

, ,.

Отже, нерівність відсікання Гоморі має вид:

.

До лівої частини нерівності додаємо змінну і записуємо таке рівняння:

або .

4. Включаємо це рівняння в систему обмежень, отриману на останньому кроці розв’язання задачі без умови цілочисловості (див. табл. 6.1), і продовжуємо вирішувати задачу, використовуючи симплекс-метод.

Так, розширена матриця системи обмежень матиме вид:

_.

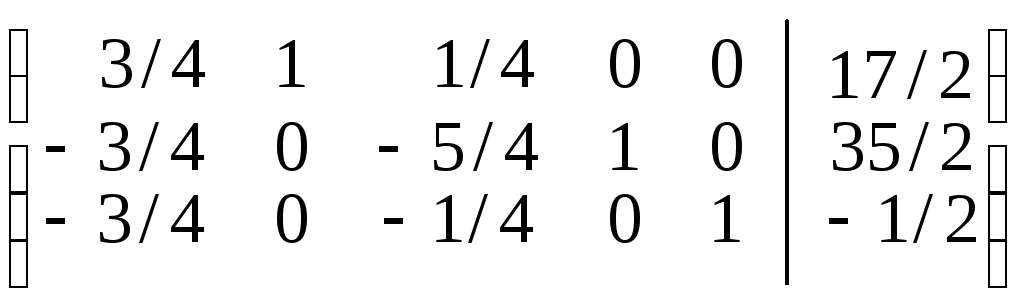Приводимо дану матрицю до одиничного базису з невід’ємними вільними членами

_.

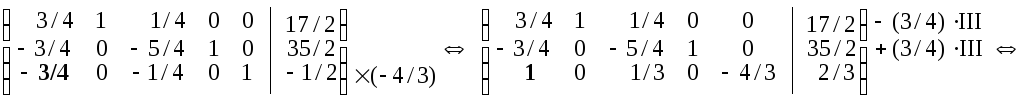
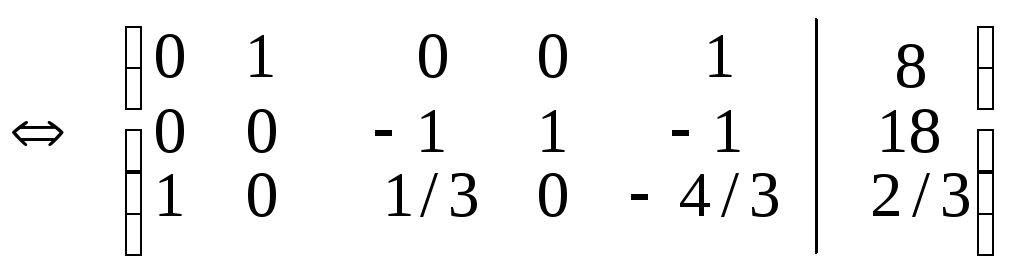Одержуємо опорний план: .

Перевіряємо даний опорний план на оптимальність за допомогою симплекс-таблиці.

Таблиця 6.2
Б	сБ	b	x1	x2	x3	x4	x5
			–2	–3	0	0	0
x2	–3	8	0	1	0	0	1
x4	0	18	0	0	–1	1	–1
x1	–2	2/3	1	0	1/3	0	–4/3
		–76/3	0	0	–2/3	0	–1/3

Опорний план є оптимальним, тому що в останньому рядку табл. 6.2 всі оцінки недодатні, але це не задовольняє умові цілочисловості.

5. Обираємо дробову компоненту 2/3.

Рівняння відповідного рядка симплекс-таблиці (табл. 7.2):

,

де – базисна змінна,,– небазисні змінні.

Виражаємо базисну змінну через небазисні змінні:

.

Записуємо нерівність відсікання Гоморі:

.

Знаходимо дробові частини чисел:

, ,.

Отже, нерівність відсікання Гоморі має вид:

.

До лівої частини нерівності додаємо змінну і записуємо таке рівняння:

або .

6. Включаємо це рівняння в систему обмежень (див. табл. 6.2) і продовжуємо розв’язувати задачу, використовуючи симплекс-метод.

Так, розширена матриця системи обмежень буде мати вид:

_.

Приводимо дану матрицю до одиничного базису з невід’ємними вільними членами

_.

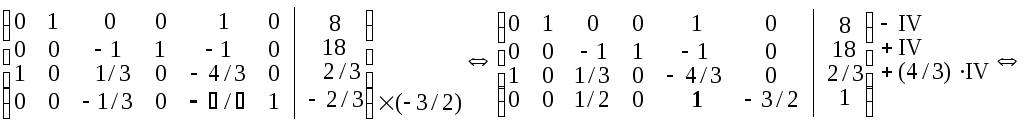
Одержуємо опорний план: .

Перевіряємо даний опорний план на оптимальність за допомогою симплекс-таблиці.

Таблиця 6.3

Б	сБ	b	x1	x2	x3	x4	x5	x6
			–2	–3	0	0	0	0
x2	–3	7	0	1	–1/2	0	0	3/2
x4	0	19	0	0	–1/2	1	0	–3/2
x1	–2	2	1	0	1	0	0	–2
x5	0	1	0	0	1/2	0	1	–3/2
		–25	0	0	–1/2	0	0	–1/2

Опорний план є оптимальним, тому що в останньому рядку табл. 6.3 всі оцінки недодатні. Крім того,задовольняє умові цілочисловості.

Оптимальне значення цільової функції: .

Отже, при оптимальному цілочисельному рішенні , тобто максимальну продуктивність 25 т сортового зерна за зміну можна одержати придбанням двох машин типуA і семи машин типу B; при цьому з виділених коштів залишки дорівнюють 0, незайнята площа приміщення складе 19 кв. м (п’ятий і шостий компоненти змістовного значення не мають).