
- •Міністерство освіти і науки України
- •Математичні моделі економічних задач
- •1.1. Задача планування виробництва
- •1.2. Задача складання раціону (задача про дієту, задача про суміші)
- •1.3. Транспортна задача
- •1.4. Задача про мінімізацію відходів
- •К 2ількість шматків
- •1.5. Задача про призначення
- •Загальна постановка задач лінійного програмування (лп)
- •Перелік питань для самоперевірки
- •Лекція 2
- •Тема 2. Геометрична інтерпретація задач лінійного програмування. Задача лінійного програмування, форми її запису
- •Приведення задачі лп до канонічного виду
- •Приведення задачі лп до симетричного виду
- •Перелік питань для самоперевірки
- •3.1. Визначення вихідного опорного плану
- •3.2. Симплексні таблиці
- •3.3. Поняття про м-метод
- •Перелік питань для самоперевірки
- •Лекція 4
- •Тема 4. Двоїстість у лінійному програмуванні
- •Перелік питань для самоперевірки
- •Лекція 5
- •Тема 5. Методика розв’язування транспортної задачі
- •5.1. Приведення задачі до замкненої форми
- •5.2. Визначення вихідного опорного плану
- •5.3. Метод потенціалів
- •Перелік питань для самоперевірки
- •6.1. Метод відсікань Гоморі
- •Перелік питань для самоперевірки
- •Лекція 6
- •Тема 7. Елементи теорії ігор
- •7.1. Графічний метод
- •7.2. Приведення матричної гри до задачі лінійного програмування
- •Перелік питань для самоперевірки
- •8.2. Задачі нелінійного програмування з нелінійною цільовою функцією та лінійною системою обмежень
- •Перелік питань для самоперевірки
- •Лекція 8
- •Тема 9. Динамічне програмування
- •9.1. Задача про розподіл коштів між підприємствами
- •Рішення
- •9.2. Задача про заміну обладнання
- •Рішення
- •Перелік питань для самоперевірки
- •Список рекомендованої літератури
7.2. Приведення матричної гри до задачі лінійного програмування
Рішення
гри mn
у загальному випадку може бути зведене
до розв’язання задачі лінійного
програмування. Нехай гра mn
задана платіжною матрицею (табл. 7.1).
Необхідно визначити оптимальні стратегії
![]() і
і
![]() ,
де
,
де
![]() –
ймовірності застосування відповідних
чистих стратегій
–
ймовірності застосування відповідних
чистих стратегій
![]() ;
;
![]() ,
,
![]() .
.
Будемо
вважати, що ціна гри
![]() ;
цього завжди можна досягти, зробив-ши
всі елементи
;
цього завжди можна досягти, зробив-ши
всі елементи
![]() (див.
зауваження 7.1).
(див.
зауваження 7.1).
Якщо
гравець A
застосовує змішану стратегію
![]() проти
будь-якої чистої стратегії
проти
будь-якої чистої стратегії
![]() гравця
B,
то він одержує середній
виграш
(математичне
очікування виграшу)
гравця
B,
то він одержує середній
виграш
(математичне
очікування виграшу)
![]() .
.
Усі середні виграші aj не менше ціни гри v, тому маємо систему нерівностей:
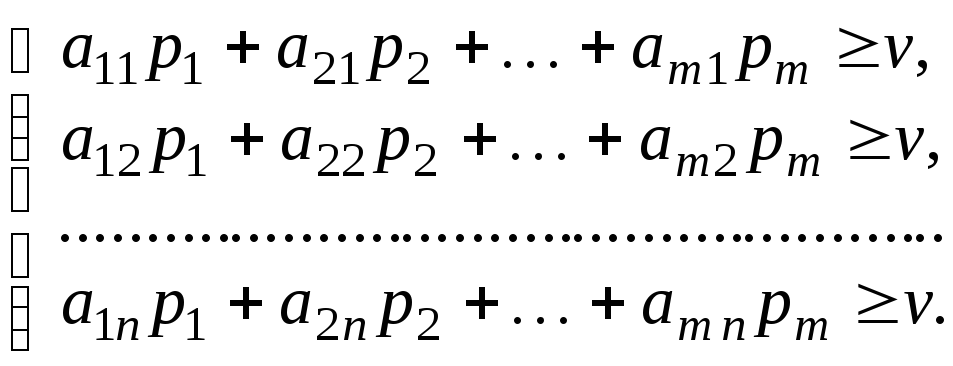 (7.1)
(7.1)
Кожну
з нерівностей поділимо на число
![]() і введемо нові змінні:
і введемо нові змінні:
![]() .
Тоді система (7.1) матиме вид:
.
Тоді система (7.1) матиме вид:
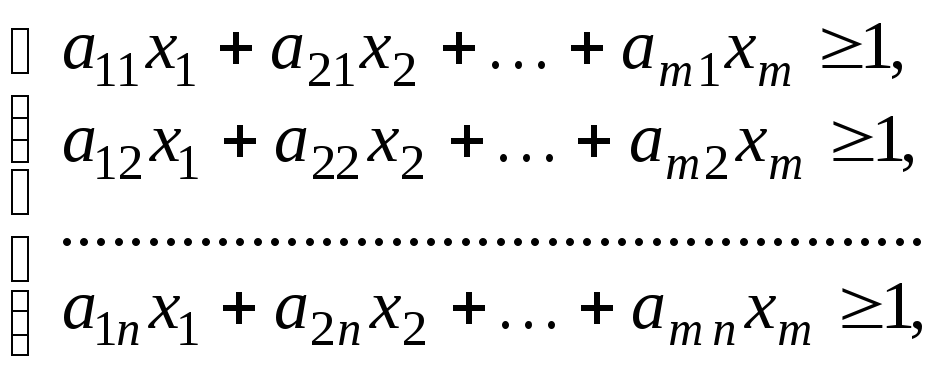
де
![]() тому що
тому що
![]() і
і
![]() .
.
Мета гравця A – максимізувати свій гарантований виграш, тобто ціну гри v.
Поділивши
на
![]() рівність
рівність
![]() ,
маємо
,
маємо
![]() .
Максимізація ціни гри v
еквівалентна мінімізації величини
.
Максимізація ціни гри v
еквівалентна мінімізації величини
![]() ,
тому задача може бути сформульована
наступним чином.
,
тому задача може бути сформульована
наступним чином.
|
Дано: |
|
(7.2) |
|
Знайти
такий план
| ||
Це
задача лінійного програмування.
Розв’язуючи задачу (7.2), отримаємо
оптимальне рішення
![]() і оптимальну стратегію
і оптимальну стратегію![]() .
.
Оптимальна
стратегія
![]() забезпечує
гравцю B
середній
програш, не більший, ніж ціна гри
v
за будь-якої стратегії гравця A.
Тому змінні
забезпечує
гравцю B
середній
програш, не більший, ніж ціна гри
v
за будь-якої стратегії гравця A.
Тому змінні
![]() задовольняють
нерівностям
задовольняють
нерівностям
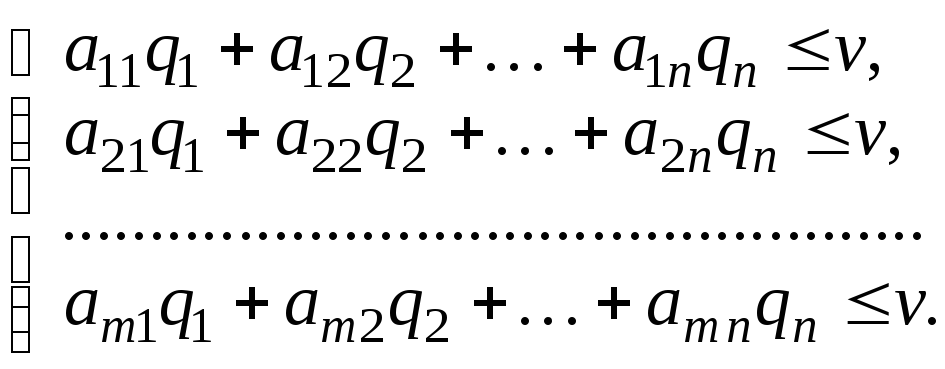
Якщо
позначити
![]() ,
то одержимо систему нерівностей:
,
то одержимо систему нерівностей:
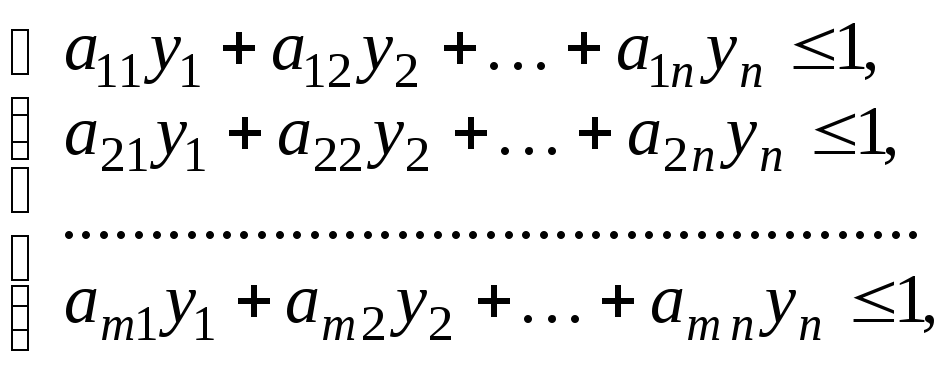
де
![]() тому
що
тому
що
![]() і
і
![]() .
.
Мета гравця B – мінімізувати свій гарантований програш, тобто ціну гри v.
Поділивши
на
![]() рівність
рівність
![]() ,
маємо
,
маємо
![]() .
Мінімізація ціни гри v
еквівалентна максимізації величини
.
Мінімізація ціни гри v
еквівалентна максимізації величини
![]() ,
тому задача може бути сформульована
наступним чином.
,
тому задача може бути сформульована
наступним чином.
|
Дано: |
|
(7.3) |
|
Знайти
такий план
| ||
Розв’язок
задачі лінійного програмування (7.3)
визначає оптимальну стратегію
![]() гравця B.
При цьому ціна гри
гравця B.
При цьому ціна гри
![]() .
.
Задачі (7.2) і (7.3) є взаємно-подвійними задачами лінійного програмування. При визначенні оптимальних стратегій у конкретних задачах варто обрати ту із взаємно-подвійних задач, розв’язання якої легше, а рішення іншої задачі знайти за допомогою теорем подвійності.
Задача 7.3. Підприємство може випускати три види продукції (A1, A2, A3), одержуючи при цьому прибуток, який залежить від попиту, що може бути в одному з чотирьох станів (B1, B2, B3, B4). Дано матрицю (табл. 7.3), її елементи aij характеризують прибуток, що одержить підприємство при випуску одиниці i-ї продукції за j-м станом попиту. Визначити оптимальні пропорції у випуску продукції за умови максимізації середнього гарантованого прибутку.
Рішення
Таблиця 7.3
|
|
B1 |
B2 |
B3 |
B4 |
|
A1 |
0 |
1 |
3 |
5 |
|
A2 |
6 |
7 |
1 |
–1 |
|
A3 |
4 |
4 |
2 |
1 |
1. Задача зводиться до ігрової моделі, у якій гра підприємства A проти попиту B задана платіжною матрицею (див. табл. 7.3).
Перш ніж розв’язувати задачу, треба спробувати спростити гру,
провівши аналіз платіжної матриці і відкинувши явно невигідні або дублюючі стратегії. Друга стратегія гравця B (другий стовпець матриці (див. табл. 7.3)) є явно невигідною для гравця B у порівнянні з першою (елементи другого стовпця більше елементів першого стовпця), оскільки мета гравця B – зменшити свій програш. Тому другий стовпець можна відкинути. Одержимо матрицю P:
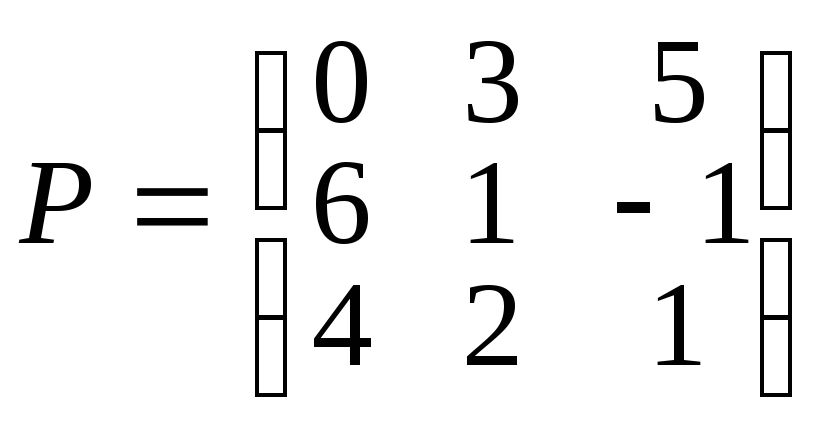 .
.
2. Визначимо нижню і верхню ціни гри P в табл. 7.4.
Таблиця 7.4
|
|
B1 |
B3 |
B4 |
i |
|
A1 |
0 |
3 |
5 |
0 |
|
A2 |
6 |
1 |
–1 |
–1 |
|
A3 |
4 |
2 |
1 |
1 |
|
|
6 |
3 |
5 |
1 3 |
Нижня
ціна гри
![]() ,
верхня ціна
,
верхня ціна
![]() .
Оскільки
.
Оскільки
![]() ,
гра не має сідлової точки, і оптимальне
рішення шукаємо в змішаних стратегіях
гравців:
,
гра не має сідлової точки, і оптимальне
рішення шукаємо в змішаних стратегіях
гравців:
![]() і
і
![]() .
.
Ціна
гри
![]() .
.
3. Матриця P даної гри має від’ємний елемент, тому переходимо до еквівалентної гри з платіжною матрицею
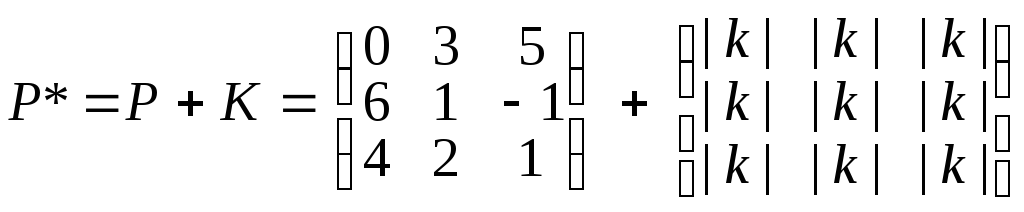 ,
,
де k
– найбільший за модулем від’ємний
елемент матриці P,
тобто
![]() (див.
зауваження 7.1).
(див.
зауваження 7.1).
Таким чином,
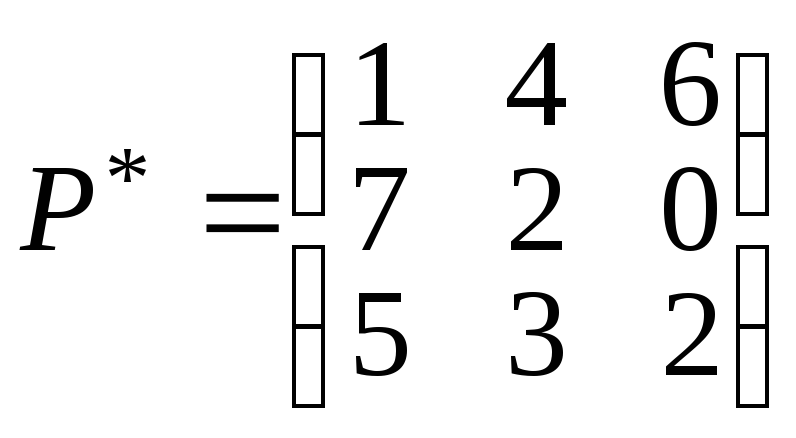 .
.
Ціна
еквівалентної гри
![]() .
.
4.
Позначивши
![]() ,
складемо дві взаємно-подвійні задачі
лінійного програмування (див.
(7.2) і (7.3)).
,
складемо дві взаємно-подвійні задачі
лінійного програмування (див.
(7.2) і (7.3)).
|
Задача 1 |
Задача 2 |
|
|
|
5. Розв’язуємо симплексним методом одну із задач, наприклад, задачу 2, тому що для неї легше отримати перший базисний розв’язок.
Приводимо задачу 2 до канонічного виду:
|
|
Будуємо розширену матрицю системи обмежень
 .
.
Базисні
змінні:
y4,
y5,
y6;
вільні змінні: y1,
y2,
y3.
Базисний розв’язок:
![]() .
Він є опорним планом (усі його компоненти
невід’ємні).
.
Він є опорним планом (усі його компоненти
невід’ємні).
Перевіряємо даний опорний план на оптимальність.
Заповнюємо першу симплексну таблицю.
Т аблиця
7.5
аблиця
7.5
|
Б |
сБ |
b |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
|
–1 |
–1 |
–1 |
0 |
0 |
0 | |||
|
y4 |
0 |
1 |
1 |
4 |
6 |
1 |
0 |
0 |
|
y5 |
0 |
1 |
7 |
2 |
0 |
0 |
1 |
0 |
|
|
0 |
1 |
5 |
3 |
2 |
0 |
0 |
1 |
|
|
0 |
1 |
1 |
1 |
0 |
0 |
0 | |
В
нижньому рядку в першій клітинці
записуємо значення цільової функції
![]() на
опорному плані
на
опорному плані
![]() ,в
інших шести клітинках – оцінки
оптимальності.
,в
інших шести клітинках – оцінки
оптимальності.
Опорний
план
![]() не
є оптимальним, тому що серед оцінок
оптимальності є додатні оцінки.
не
є оптимальним, тому що серед оцінок
оптимальності є додатні оцінки.
Переходимо
до нового опорного плану. Змінним y1,
y2,
y3
відповідають
однакові додатні оцінки оптимальності,
які дорівнюють 1. Тому вводимо в базис
одну з цих змінних, наприклад, y2.
Змінну y4
виводимо
з базису, тому що їй відповідає мінімальне
значення із симплексних відносин:
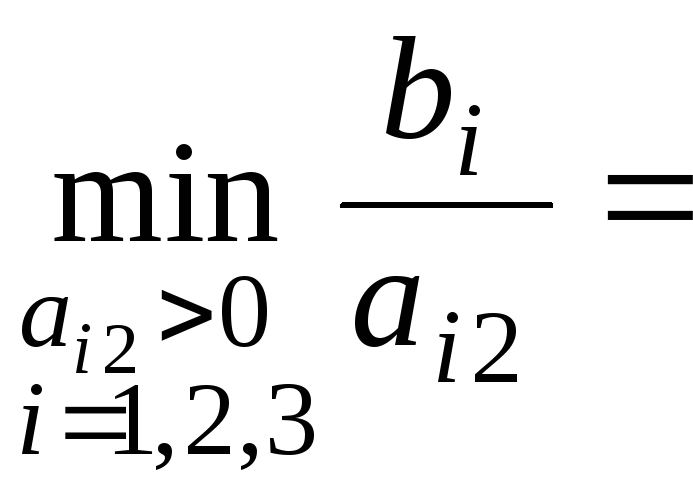
![]() .За
допомогою елементарних перетворень у
другому стовпці розширеної матриці
будуємо одиничний вектор, у якого 1
розташована в ключовому рядку I.
.За
допомогою елементарних перетворень у
другому стовпці розширеної матриці
будуємо одиничний вектор, у якого 1
розташована в ключовому рядку I.

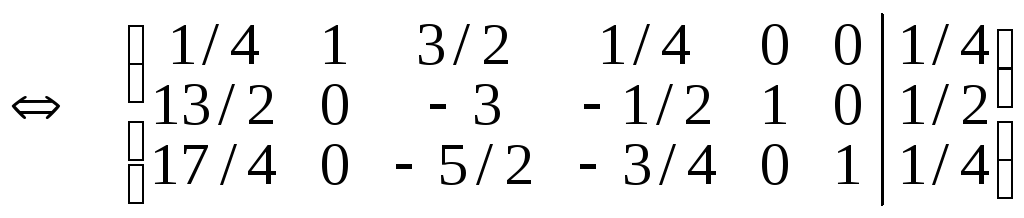 .
.
Базисні
змінні:
y2,
y5,
y6;
вільні змінні: y1,
y3,
y4.
Новий базисний розв’язок
![]() – новий опорний план.
– новий опорний план.
Заповнюємо другу симплекс-таблицю.

Таблиця 7.6
|
Б |
сБ |
b |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
|
–1 |
–1 |
–1 |
0 |
0 |
0 | |||
|
y2 |
–1 |
1/4 |
1/4 |
1 |
3/2 |
1/4 |
0 |
0 |
|
y5 |
0 |
1/2 |
13/2 |
0 |
–3 |
–1/2 |
1 |
0 |
|
|
0 |
1/4 |
17/4 |
0 |
–5/2 |
–3/4 |
0 |
1 |
|
|
–1/4 |
3/4 |
0 |
–1/2 |
–1/4 |
0 |
0 | |
Опорний
план
![]() не
є оптимальним, тому що серед оцінок
оптимальності є додатна оцінка 3/4.
не
є оптимальним, тому що серед оцінок
оптимальності є додатна оцінка 3/4.
Знов
переходимо до нового опорного плану.
Змінну y1
вводимо
в базис, оскільки цій змінній відповідає
додатна оцінка 3/4. Змінну y4
виводимо
з базису, тому що їй відповідає мінімальне
значення із симплексних відносин:
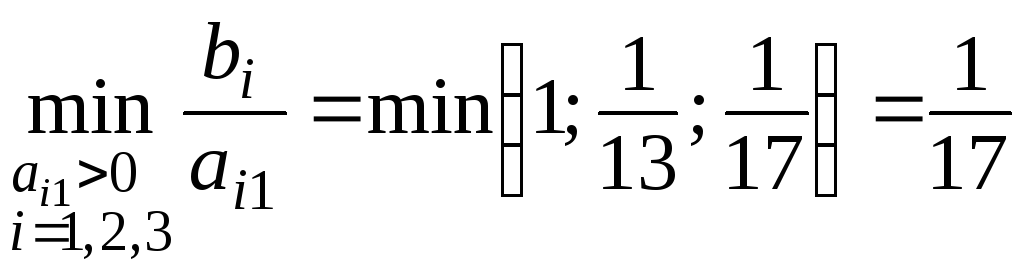 .За
допомогою елементарних перетворень у
першому стовпці розширеної матриці
будуємо одиничний вектор, у якого 1
знаходиться в ключовому рядку III.
.За
допомогою елементарних перетворень у
першому стовпці розширеної матриці
будуємо одиничний вектор, у якого 1
знаходиться в ключовому рядку III.

 .
.
Базисні
змінні:
y1,
y2,
y5;
вільні змінні: y3,
y4,
y6.
Базисний розв’язок
![]() – новий опорний план.
– новий опорний план.
Заповнюємо третю симплекс-таблицю:
Таблиця 7.7
|
Б |
сБ |
b |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
|
–1 |
–1 |
–1 |
0 |
0 |
0 | |||
|
y2 |
–1 |
4/17 |
0 |
1 |
28/17 |
5/17 |
0 |
–1/17 |
|
y5 |
0 |
2/17 |
0 |
0 |
14/17 |
11/17 |
1 |
–26/17 |
|
y1 |
–1 |
1/17 |
1 |
0 |
–10/17 |
–3/17 |
0 |
4/17 |
|
|
–5/17 |
0 |
0 |
–1/17 |
–2/17 |
0 |
–3/17 | |
Опорний
план
![]() є
оптимальним, тому що в останньому рядку
всі оцінки недодатні. Отже,
є
оптимальним, тому що в останньому рядку
всі оцінки недодатні. Отже,
![]() ,
,
![]() ,
,
![]() .
.
6.
За отриманими результатами знаходимо
ціну еквівалентної гри
![]() й
оптимальну стратегію
й
оптимальну стратегію
![]() :
:
![]() ,
,
![]() ,
,
![]() ;
;
![]() .
.
7.
Визначимо оптимальний розв’язок задачі
1 за допомогою теорем подвійності. На
основі першої теореми подвійності
![]() .
На основі другої теореми подвійності
компоненти
.
На основі другої теореми подвійності
компоненти
![]() оптимального
розв’язку задачі 1 дорівнюють абсолютним
значенням оцінок оптимальності, що
відповідають змінним
оптимального
розв’язку задачі 1 дорівнюють абсолютним
значенням оцінок оптимальності, що
відповідають змінним
![]() ,
у підсумковій симплекс-таблиці 7.7.
,
у підсумковій симплекс-таблиці 7.7.
![]() ,
,
![]() ,
,
![]() .
.
За цими
даними знаходимо оптимальну стратегію
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Повертаючись до вихідної гри, одержимо оптимальну ціну
![]() .
.
Висновок:
оптимальна стратегія підприємства
![]() ,
тобто підприємство має випустити 40%
продукції
A1
і
60% продукції
A3,
а продукцію A2
не
випускати. Оптимальна стратегія попиту
,
тобто підприємство має випустити 40%
продукції
A1
і
60% продукції
A3,
а продукцію A2
не
випускати. Оптимальна стратегія попиту
![]() (тут
враховано, що другий стовпець вихідної
матриці був відкинутий як невигідний),
тобто оптимальний попит у 20% перебуває
в стані
B1
і
в
80%
– у стані B3.
(тут
враховано, що другий стовпець вихідної
матриці був відкинутий як невигідний),
тобто оптимальний попит у 20% перебуває
в стані
B1
і
в
80%
– у стані B3.
При вирішенні довільної кінцевої гри розміру mn доцільно дотримуватись наступної схеми:
Виключити з платіжної матриці явно невигідні стратегії в порівнянні з іншими стратегіями. Такими стратегіями для гравця A (гравця B) є ті, котрим відповідають рядки (стовпці) з елементами, меншими (більшими) у порівнянні з відповідними елементами деякого з інших рядків (стовпців).
Визначити верхню і нижню ціни гри і перевірити, чи має гра сідлову точку. Якщо сідлова точка є, то відповідні їй стратегії гравців будуть оптималь-ними, а ціна гри збігатиметься з верхньою та нижньою ціною.
Якщо гра не має сідлової точки, то рішення треба шукати в змішаних стратегіях. Для ігор розміру mn рекомендується симплекс-метод, для ігор розміру 22, 2 n, n 2 можливе геометричне рішення.

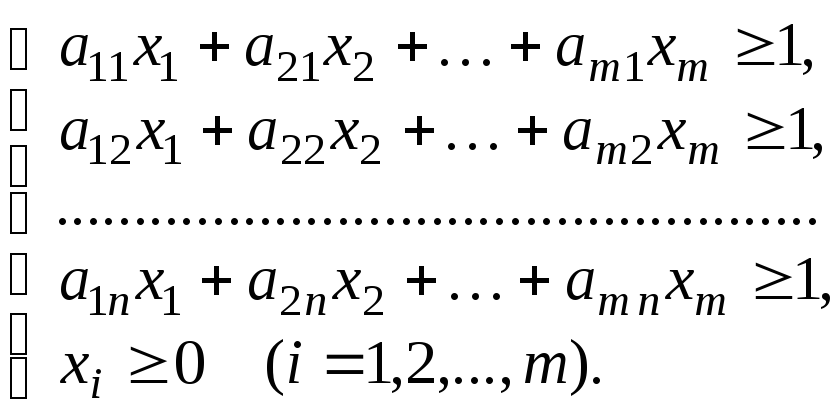
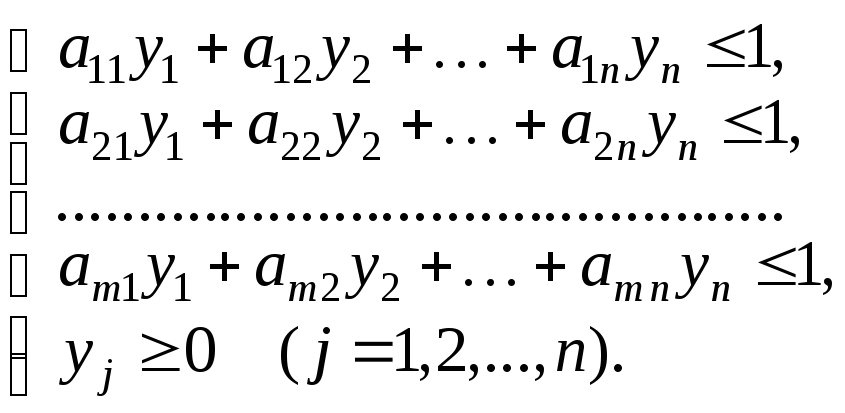
 j
j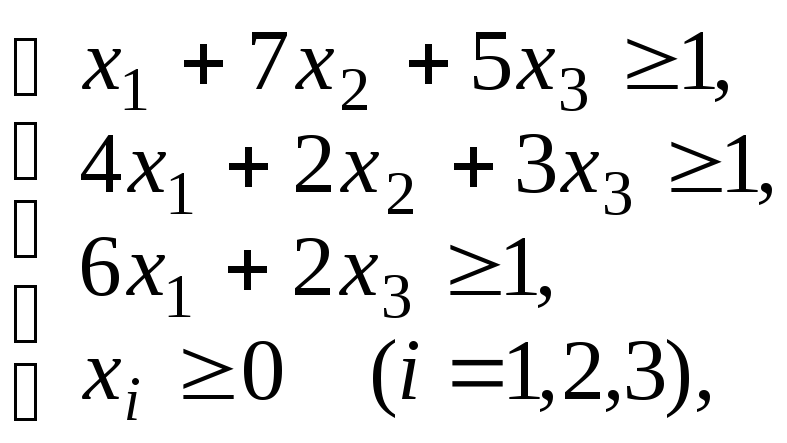
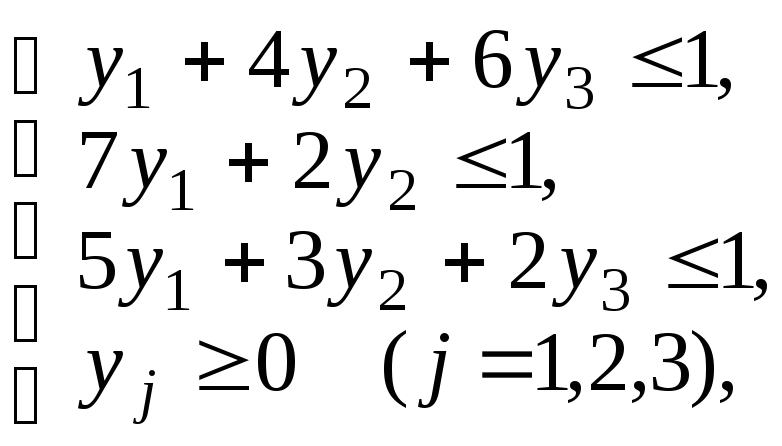

 y6
y6 y6
y6