
- •Міністерство освіти і науки України
- •Математичні моделі економічних задач
- •1.1. Задача планування виробництва
- •1.2. Задача складання раціону (задача про дієту, задача про суміші)
- •1.3. Транспортна задача
- •1.4. Задача про мінімізацію відходів
- •К 2ількість шматків
- •1.5. Задача про призначення
- •Загальна постановка задач лінійного програмування (лп)
- •Перелік питань для самоперевірки
- •Лекція 2
- •Тема 2. Геометрична інтерпретація задач лінійного програмування. Задача лінійного програмування, форми її запису
- •Приведення задачі лп до канонічного виду
- •Приведення задачі лп до симетричного виду
- •Перелік питань для самоперевірки
- •3.1. Визначення вихідного опорного плану
- •3.2. Симплексні таблиці
- •3.3. Поняття про м-метод
- •Перелік питань для самоперевірки
- •Лекція 4
- •Тема 4. Двоїстість у лінійному програмуванні
- •Перелік питань для самоперевірки
- •Лекція 5
- •Тема 5. Методика розв’язування транспортної задачі
- •5.1. Приведення задачі до замкненої форми
- •5.2. Визначення вихідного опорного плану
- •5.3. Метод потенціалів
- •Перелік питань для самоперевірки
- •6.1. Метод відсікань Гоморі
- •Перелік питань для самоперевірки
- •Лекція 6
- •Тема 7. Елементи теорії ігор
- •7.1. Графічний метод
- •7.2. Приведення матричної гри до задачі лінійного програмування
- •Перелік питань для самоперевірки
- •8.2. Задачі нелінійного програмування з нелінійною цільовою функцією та лінійною системою обмежень
- •Перелік питань для самоперевірки
- •Лекція 8
- •Тема 9. Динамічне програмування
- •9.1. Задача про розподіл коштів між підприємствами
- •Рішення
- •9.2. Задача про заміну обладнання
- •Рішення
- •Перелік питань для самоперевірки
- •Список рекомендованої літератури
Перелік питань для самоперевірки
Математична постановка задач цілочислового (дискретного) програмування.
Метод відсікань Гоморі.
Лекція 6
Тема 7. Елементи теорії ігор
В даній темі розглядаються кінцеві ігри двох осіб з нульовою сумою (виграш одного з гравців дорівнює програшу іншого).
Вихідною
інформацією для такої гри є платіжна
матриця
![]() i=1,…,m;
j=1,…,n,
загальний вид якої наведений у табл.
7.1.
i=1,…,m;
j=1,…,n,
загальний вид якої наведений у табл.
7.1.
Таблиця 7.1
|
|
B1 |
B2 |
… |
Bn |
|
A1 |
a11 |
a12 |
… |
a1n |
|
A2 |
a21 |
a22 |
… |
a2n |
|
… |
… |
… |
… |
… |
|
Am |
am1 |
am2 |
… |
amn |
Ця матриця інтерпретується наступним чином. Гравець A має m стратегій: A1, A2,…, Am (рядки матриці). Гравець B має n стратегій: B1, B2,…, Bn (стовпці матриці). У результаті вибору гравцями будь-якої пари стратегій Ai і Bj (i=1,…, m; j=1,…, n) однозначно визна-
чається результат гри, тобто виграш aij гравця A (додатний чи від’ємний) і програш (aij) гравця В.
Величину
![]()
називають нижньою ціною гри. Це максимальний гарантований виграш гравця A при будь-якій стратегії гравця B.
Величину
![]()
називають верхньою ціною гри. Це мінімальний гарантований програш гравця B.
Рішення матричної гри (табл. 7.1) полягає у пошуку оптимальних стратегій для кожного гравця, тобто стратегій, при виборі яких гравець A одержує максимальний гарантований (не залежний від поведінки гравця В) виграш, а гравець В отримує мінімальний гарантований (незалежний від поведінки гравця A) програш (принцип мінімакса). Виграш, що відповідає оптимальному рішенню, називається ціною гри v.
Завжди
має місце нерівність
![]() .
.
Якщо
верхня і нижня ціни гри збігаються (![]() ),
то говорять, що гра має сідлову
точку,
тобто елемент akl,
що є одночасно найбільшим у своєму
стовпці і найменшим у своєму рядку.
Відповідна цьому елементу пара чистих
стратегій Ak
і Bl
дає оптимальне рішення гри.
),
то говорять, що гра має сідлову
точку,
тобто елемент akl,
що є одночасно найбільшим у своєму
стовпці і найменшим у своєму рядку.
Відповідна цьому елементу пара чистих
стратегій Ak
і Bl
дає оптимальне рішення гри.
Задача 7.1. Визначити нижню і верхню ціну гри, заданою платіжною матрицею
 .
.
Чи має гра сідлову точку?
Рішення
Таблиця 7.2
|
|
B1 |
B2 |
B3 |
i |
|
A1 |
0,5 |
0,6 |
0,8 |
0,5 |
|
A2 |
0,9 |
0,7 |
0,8 |
0,7 |
|
A3 |
0,7 |
0,6 |
0,6 |
0,6 |
|
j |
0,9 |
0,7 |
0,8 |
==0,7 |
Усі розрахунки зручно звести в таблицю, до якої, крім матриці P, додається стовпець i і рядок j (табл. 7.2), де
![]() ,
,
![]() .
.
Аналізуючи
рядки матриці (стратегії гравця A),
заповнюємо стовпець i:
1=
0,5,
2=
0,7,
3=
0,6 –
мінімальні числа в рядках 1, 2, 3. Аналізуючи
стовпці матриці (стратегії гравця B),
заповнюємо рядок j:
1=
0,9,
2=
0,7,
3=
0,8 –
максимальні числа в стовпцях 1, 2, 3
відповідно. Нижня ціна гри
![]() – найбільше число в стовпці i.
Верхня ціна гри
– найбільше число в стовпці i.
Верхня ціна гри
![]() – найменше число в рядку j.
Ці значення рівні, тобто
– найменше число в рядку j.
Ці значення рівні, тобто
![]() ,
і досягаються на одній і тій же парі
стратегій (A2,B2).
Отже, гра має сідлову точку (A2,B2)
і її ціна
,
і досягаються на одній і тій же парі
стратегій (A2,B2).
Отже, гра має сідлову точку (A2,B2)
і її ціна
![]() .
Це означає, що гравець A
при постійному використанні стратегії
A2
одержує
максимальний гарантований виграш, що
дорівнює 0.7, а гравець B
при постійному використанні стратегії
B2
одержує
мінімальний гарантований програш.
.
Це означає, що гравець A
при постійному використанні стратегії
A2
одержує
максимальний гарантований виграш, що
дорівнює 0.7, а гравець B
при постійному використанні стратегії
B2
одержує
мінімальний гарантований програш.
У
випадку, коли гра не має сідлової точки
(![]() ),
можна отримати оптимальне рішення,
відповідним чином чергуючи чисті
стратегії.
),
можна отримати оптимальне рішення,
відповідним чином чергуючи чисті
стратегії.
Змішаною
стратегією
SA
гравця
A
називається
застосування чистих стратегій A1,…,
Am
з
ймовірностями
p1,…,
pm,
причому
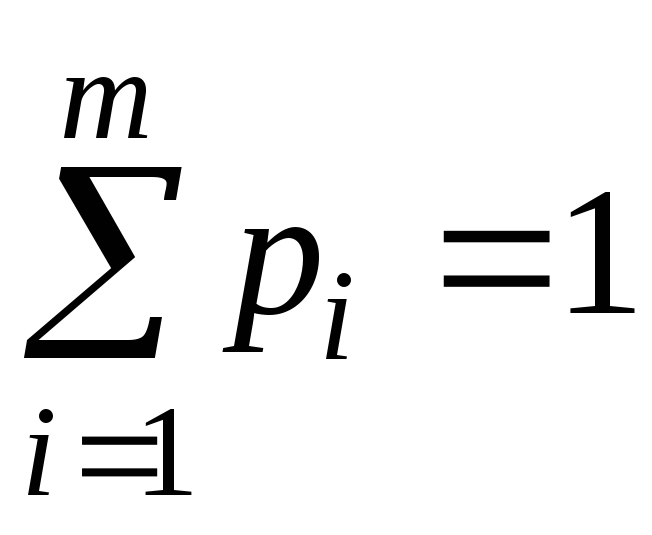 . Змішані стратегії гравця A
записуються символом
. Змішані стратегії гравця A
записуються символом
 , або
, або
![]() .
.
Аналогічно змішані стратегії гравця B позначаються як
 , або
, або
![]() ,
,
де сума
ймовірностей дорівнює 1:
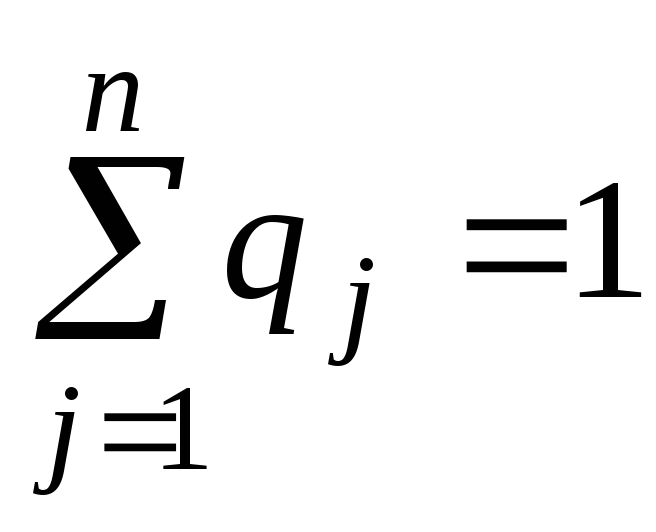 .
.
Чисті
стратегії можна вважати окремим випадком
змішаних і задавати одиничним вектором,
у якому 1 відповідає чистій стратегії.
Наприклад,
![]() .
.
Зауваження 7.1. Якщо платіжна матриця P містить від’ємні елементи, то для розв’язання задачі у змішаних стратегіях варто перейти до еквівалентної матриці з невід’ємними елементами. Для цього до всіх елементів вихідної матриці треба додати число |k|, де k – найбільший за модулем від’ємний елемент матриці P. При цьому рішення задачі не зміниться, а ціна гри збільшиться на величину |k|.
Ігри розміру 22, 2n, n2 можна розв’язати графічним методом.
Розв’язок будь-якої гри mn може бути зведений до рішення задачі лінійного програмування.
