
- •1. Потужність множини. Зчисленні множини та їх властивості. Множини n, z, q, r та їхні потужності.
- •2. Числова послідовність та її границя. Основні властивості границі. Границя обмеженої монотонної послідовності. Число е.
- •3. Дійсна функція дійсної змінної. Границя функції дійсної змінної у точці. Властивості границь.
- •4. Неперервність функції у точці. Приклади неперервних функцій. Властивості неперервних функцій.
- •5. Неперервність функції на множині. Властивості неперервних функцій на обмежених замкнених множинах.
- •6. Похідна функції дійсної змінної та її основні властивості. Диференційовність і диференціал функції
- •8. Основні теореми диференціального числення. Теореми Ролля, Лагранжа й Коші. Формула Тейлора.
- •9. Застосування диференціального числення до дослідження властивостей функції. Умови сталості і монотонності функції на проміжку. Екстремуми функції.
- •Достатні умови існування екстремуму функції. Теорема. Нехай критична точка функції ,неперервна в точціі має похіднув усіх точках околуза виключенням, можливо самої точки. Тоді
- •10. Застосування диференціального числення до дослідження властивостей функцій. Опуклість і точки перегину.
- •11. Первісна та її властивості. Невизначений інтеграл. Основні способи інтегрування. Таблиця невизначених інтегралів від основних елементарних функцій.
- •12. Інтеграла Рімана для функції однієї змінної. Основні властивості.
- •13 Критерій інтегровності. Основні класи інтегровних за Ріманом функцій.
- •14 Показникова і логарифмічна функції дійсних чисел.
- •15 Розвиток поняття степеня з дійсним показником. Властивості степеня. Загальна степенева функція дійсної змінної (озн, вл, графік).
- •16 Тригонометричні та обернені тригонометричні функції дійсної зміної (означення неперервність, властивості, графік).
- •18. N-вимірний евклідів простір як узагальнення просторів
- •19 Числові ряди. Геометрична прогресія та гармонійний ряд. Властивості збіжних рядів.
- •20 Додатні ряди, основні ознаки збіжності додатніх рядів. Ряди з довільними членами. Абсолютно і умовно збіжні ряди.
1. Потужність множини. Зчисленні множини та їх властивості. Множини n, z, q, r та їхні потужності.
Множина
 ,
яка складається із скінченного числа
елементів, називається скінченною
(число її
елементів позначається
,
яка складається із скінченного числа
елементів, називається скінченною
(число її
елементів позначається
 ).
Скінченні множини можна порівнювати
за кількістю їх елементів.
Для порівняння нескінченних множин Г.
Кантор побудував теорію вихідним пунктом
якої є поняття потужності множини.
).
Скінченні множини можна порівнювати
за кількістю їх елементів.
Для порівняння нескінченних множин Г.
Кантор побудував теорію вихідним пунктом
якої є поняття потужності множини.
Множини
 і
і називаються рівнопотужними (мають
однакову потужність), якщо існує бієкція
називаються рівнопотужними (мають
однакову потужність), якщо існує бієкція .
Рівнопотужні множини позначають так:A
~ B.
.
Рівнопотужні множини позначають так:A
~ B.
Зчисленні множини
. Множина
 називається зчисленною, якщоA
~ N.
У цьому випадку говорять, що елементи
множини
називається зчисленною, якщоA
~ N.
У цьому випадку говорять, що елементи
множини
 можна занумерувати.
Мають місце
наступні твердження:
можна занумерувати.
Мають місце
наступні твердження:
Нескінченна підмножина зчисленної множини зчисленна.
Нескінченна множина містить зчисленну підмножину.
Об'єднання зчисленної множини зчисленних множин є зчисленною множиною.
Декартів добуток двох зчисленних множин зчисленний.
Існують незчисленні множини.
Спинимось на доведенні твердження 3.
Нехай
 -
зчисленні множини. Тоді для кожного
-
зчисленні множини. Тоді для кожного .
.
Елементи об'єднання
 цих множин можна подати у вигляді таблиці
цих множин можна подати у вигляді таблиці







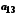 …
… …
…





 …
… …
…


 …
… …
…
…………………………………………
і занумерувати,
наприклад у порядку, вказаному стрілками.
Цим саме буде встановлена бієкція
 .
Отже,
.
Отже, .
.
Аналогічно доводиться твердження 4.
Нехай
 .
Тоді декартів добуток
.
Тоді декартів добуток складається із пар, які можна розташувати
в такому порядку
складається із пар, які можна розташувати
в такому порядку

і занумерувати так, як зроблено в попередньому випадку. Для доведення твердження 5 застосуємо діагональний метод (діагональну процедуру) Кантора.
Нехай
 − множина всіх можливих нескінченних
ланцюгів, що складаються з двох символів,
наприклад 0 і 1, вигляду
− множина всіх можливих нескінченних
ланцюгів, що складаються з двох символів,
наприклад 0 і 1, вигляду
Покажемо, що
множина
 незчисленна. Припустимо, що елементи
множини
незчисленна. Припустимо, що елементи
множини занумеровані, тобто що множина
занумеровані, тобто що множина зчисленна. Нехай
зчисленна. Нехай

де кожне
 дорівнює 0 або 1. Утворимо елемент
дорівнює 0 або 1. Утворимо елемент ,
поклавши
,
поклавши ,
і кожне
,
і кожне відповідно дорівнює 0 або 1. Очевидно,
що
відповідно дорівнює 0 або 1. Очевидно,
що ,
але не збігається з жодним із занумерованих
елементів
,
але не збігається з жодним із занумерованих
елементів .
А це суперечить тому, що всі елементи
множини
.
А це суперечить тому, що всі елементи
множини можна занумерувати.
Множини N,
Z,
Q
(h=m+n)
– зчисленні,
а множина R
– незчисленна.
можна занумерувати.
Множини N,
Z,
Q
(h=m+n)
– зчисленні,
а множина R
– незчисленна.
2. Числова послідовність та її границя. Основні властивості границі. Границя обмеженої монотонної послідовності. Число е.
Якщо
кожному натуральному числові
 поставлено у відповідність дійсне число
поставлено у відповідність дійсне число ,
то множина дійсних чисел
,
то множина дійсних чисел (1) називається числовою послідовністю.(Числовою
послідовністю називається відображення
(1) називається числовою послідовністю.(Числовою
послідовністю називається відображення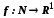 або, як кажуть – це функція задана на
множині натуральних чисел).Числа
або, як кажуть – це функція задана на
множині натуральних чисел).Числа
 називаються елементами (або членами)
послідовності. Символ
називаються елементами (або членами)
послідовності. Символ називається загальним елементом
послідовності, а
називається загальним елементом
послідовності, а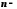 його номером. Скорочено послідовність
(1) позначається так:
його номером. Скорочено послідовність
(1) позначається так: .
Послідовність
вважається заданою, якщо вказано правило,
за яким кожному натуральному числові
.
Послідовність
вважається заданою, якщо вказано правило,
за яким кожному натуральному числові
 поставлено у відповідність дійсне
число
поставлено у відповідність дійсне
число .
Задаються за допомогою формул, рекурентних
формул.
.
Задаються за допомогою формул, рекурентних
формул.
Арифм.
дії над послід: Добутком послідовності
 на число
на число називається послідовність
називається послідовність ;
Сумою послідовностей
;
Сумою послідовностей і
і називається послідовність
називається послідовність ,
різницею – послідовність
,
різницею – послідовність ,
добутком – послідовність
,
добутком – послідовність ,
часткою
послідовність
,
часткою
послідовність
 .
.
Послідовність
 називається обмеженою зверху, якщо
існує таке число
називається обмеженою зверху, якщо
існує таке число ,
що для всіх її членів
,
що для всіх її членів виконується нерівність
виконується нерівність
Послідовність
 називається обмеженою знизу, якщо існує
таке число
називається обмеженою знизу, якщо існує
таке число ,
що для всіх її членів
,
що для всіх її членів виконується нерівність
виконується нерівність
Послідовність
 називається обмеженою, якщо вона обмежена
зверху й знизу.
називається обмеженою, якщо вона обмежена
зверху й знизу.
Нехай
послідовність
 обмежена, тобто існують такі числа
обмежена, тобто існують такі числа і
і ,
що для будь-якого її члена
,
що для будь-якого її члена виконується нерівність
виконується нерівність Нехай
Нехай .
Тоді умову обмеженості послідовності
можна записати так:
.
Тоді умову обмеженості послідовності
можна записати так: .
.
Послідовність
 називається необмеженою, якщо для
будь-якого числа
називається необмеженою, якщо для
будь-якого числа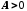 існує елемент
існує елемент цієї послідовності, для якого виконується
нерівність
цієї послідовності, для якого виконується
нерівність .
(Необмежена послідовність може бути
обмеженою зверху або знизу.)
.
(Необмежена послідовність може бути
обмеженою зверху або знизу.)
Послідовність
 називається
нескінченно великою, якщо для будь-якого
числа
називається
нескінченно великою, якщо для будь-якого
числа
 існує такий номер
існує такий номер ,
що для всіх елементів
,
що для всіх елементів із номером
із номером виконується нерівність
виконується нерівність .
.
Послідовність
 називається нескінченно малою, якщо
для будь-якого (як завгодно малого) числа
називається нескінченно малою, якщо
для будь-якого (як завгодно малого) числа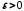 існує такий номер
існує такий номер ,
що для всіх елементів
,
що для всіх елементів із номером
із номером виконується нерівність
виконується нерівність .
.
Властивості
послідовностей: Якщо
 нескінченно велика
послідовність і всі її члени відмінні
від нуля, то послідовність
нескінченно велика
послідовність і всі її члени відмінні
від нуля, то послідовність нескінченно мала, і, навпаки, якщо
нескінченно мала, і, навпаки, якщо нескінченно мала
послідовність й
нескінченно мала
послідовність й ,
то послідовність
,
то послідовність нескінченно велика; сума, різниція
добуток двох нескінченно малих
послідовностей – є нескінченномалою
послідовністю; добуток обмеженої
послідовності на нескінченно малу є
нескінченно малою послідовністю.
нескінченно велика; сума, різниція
добуток двох нескінченно малих
послідовностей – є нескінченномалою
послідовністю; добуток обмеженої
послідовності на нескінченно малу є
нескінченно малою послідовністю.
Границя числової
послідовності.
Число
 називається границею послідовності
називається границею послідовності ,
якщо для будь-якого числа
,
якщо для будь-якого числа існує такий номер
існує такий номер ,
що для всіх членів послідовності
,
що для всіх членів послідовності із номером
із номером виконується нерівність
виконується нерівність
 (2).
Якщо число
(2).
Якщо число
 є границею послідовності
є границею послідовності ,
то пишуть
,
то пишуть ,
а саму
послідовність називають збіжною.
Послідовність, яка не є збіжною,
називається розбіжною.
,
а саму
послідовність називають збіжною.
Послідовність, яка не є збіжною,
називається розбіжною.
Якщо
послідовність
 збіжна і
збіжна і![]() ,
то будь-який її елемент
,
то будь-який її елемент можна подати у вигляді
можна подати у вигляді![]() ,
де
,
де -
елемент нескінченно малої послідовності
-
елемент нескінченно малої послідовності![]() .
(Дійсно, якщо
.
(Дійсно, якщо ,
то послідовність
,
то послідовність![]() є нескінченно малою, оскільки для
будь-якого
є нескінченно малою, оскільки для
будь-якого існує такий номер
існує такий номер ,
що для
,
що для виконується нерівність
виконується нерівність![]() ,
тобто
,
тобто .)
Має місце й обернене твердження. Якщо
.)
Має місце й обернене твердження. Якщо![]() можна подати у вигляді
можна подати у вигляді ,
де
,
де
нескінченно мала послідовність, то
нескінченно мала послідовність, то
 .
(Нерівність (2) рівносильна нерівності
.
(Нерівність (2) рівносильна нерівності або
або ,
із якої випливає, що
,
із якої випливає, що знаходиться в
знаходиться в околі
точки
околі
точки ).
Отже, означення границі числової
послідовності можна дати наступним
чином.
).
Отже, означення границі числової
послідовності можна дати наступним
чином.
Число
 називається границею послідовності
називається границею послідовності ,
якщо для будь-якого числа
,
якщо для будь-якого числа існує такий номер
існує такий номер ,
що всі члени послідовності
,
що всі члени послідовності із номером
із номером знаходяться в
знаходяться в околі
точки
околі
точки .
.
Властивості
збіжних послідовностей:
збіжна
послідовність має єдину границю
(викор представ.
![]() від супротив ); якщо послідовність
від супротив ); якщо послідовність збіжна, то вона обмежена (не всяка
обмежена послідовність є збіжною); якщо
збіжна, то вона обмежена (не всяка
обмежена послідовність є збіжною); якщо і
і
збіжні послідовності, то: послідовність
суми (різниці, добутку) збіжних
послідовностей
збіжні послідовності, то: послідовність
суми (різниці, добутку) збіжних
послідовностей
 та
та ,
збіжна і її границя дорівнює сумі
(різниці, добутку) границь цих
послідовностей, тобто
,
збіжна і її границя дорівнює сумі
(різниці, добутку) границь цих
послідовностей, тобто
 (
( );
послідовність
);
послідовність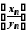 ,
яка є часткою збіжних послідовностей
,
яка є часткою збіжних послідовностей та
та ,
за умови
,
за умови , збіжна і її границя дорівнює частці
границь цих послідовностей, тобто
, збіжна і її границя дорівнює частці
границь цих послідовностей, тобто .
Типи невизначеностей:
.
Типи невизначеностей: .
.
Монотонні
послідовності Послідовність
 називається неспадною ( незростаючою
), якщо виконується нерівність
називається неспадною ( незростаючою
), якщо виконується нерівність для усіх
для усіх .
Неспадні та незростаючі послідовності
називаються монотонними.
.
Неспадні та незростаючі послідовності
називаються монотонними.
Теорема: Монотонна обмежена послідовність збіжна.
Доведення.
Розглянемо випадок неспадної послідовності
 .
.
Отже, нехай для
усіх
 виконуються наступні умови:
виконуються наступні умови:
 ;
2) існує
таке число
;
2) існує
таке число
 ,
що
,
що .
.
Розглянемо числову
множину
 ,
яка складається з усіх елементів
послідовності
,
яка складається з усіх елементів
послідовності .
За умовою ця множина непорожня і обмежена
зверху, а тому має точну верхню межу.
.
За умовою ця множина непорожня і обмежена
зверху, а тому має точну верхню межу.
Позначимо
 .
Покажемо, що
.
Покажемо, що .
.
Оскільки

точна верхня межа елементів послідовності
точна верхня межа елементів послідовності
 ,
то, згідно з властивістю точної верхньої
межі, для будь-якого
,
то, згідно з властивістю точної верхньої
межі, для будь-якого існує номер
існує номер такий, що
такий, що .
Так як послідовність
.
Так як послідовність неспадна, то при
неспадна, то при виконується нерівність
виконується нерівність .
З іншого боку, згідно з означенням точної
верхньої межі,
.
З іншого боку, згідно з означенням точної
верхньої межі,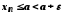 для всіх
для всіх .
Таким чином, при
.
Таким чином, при маємо нерівність
маємо нерівність ,
тобто
,
тобто при
при .
Отже,
.
Отже, .
.
Для випадку незростаючої послідовності доведення аналогічне.
Число е.
Розглянемо
послідовність з загальним членом
 .
Покажемо, що ця послідовність є збіжною.
Для цього спочатку установимо, що вона
зростаюча, а потім – що вона обмежена.
.
Покажемо, що ця послідовність є збіжною.
Для цього спочатку установимо, що вона
зростаюча, а потім – що вона обмежена.
Згідно формули
бінома Ньютона Подамо цей вираз у наступному вигляді
Подамо цей вираз у наступному вигляді
 (3)
Так само
одержуємо
(3)
Так само
одержуємо
 .
.
При
 виконується нерівність
виконується нерівність ,
тому
,
тому ,
тобто послідовність зростаюча.
Оскільки
кожний вираз, який стоїть у дужках у
формулі (3) менший від одиниці і
,
тобто послідовність зростаюча.
Оскільки
кожний вираз, який стоїть у дужках у
формулі (3) менший від одиниці і
 при
при ,
то
,
то .
За формулою
суми нескінченно спадної геометричної
прогресії маємо
.
За формулою
суми нескінченно спадної геометричної
прогресії маємо
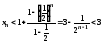 .
Отже,
послідовність
монотонна і
обмежена. Таким чином, послідовність
із загальним членом
.
Отже,
послідовність
монотонна і
обмежена. Таким чином, послідовність
із загальним членом
 збіжна. За означенням границю цієї
послідовності позначають буквою
збіжна. За означенням границю цієї
послідовності позначають буквою .
.
