3.1. Жылдам түсу əдісі

Айталық

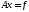
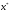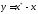теңдеулер жүйесінде А – оң анықталған симметриялы матрица жүйенің шешуі, қателік вектор, ал

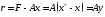
торы болсын, онда

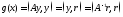(3.2)

функциясын қателер функциясы дейміз.

Мұнда (,) – скалярлық көбейтіндінің белгісі 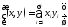A оң анықталған болғандықтан 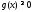жəне 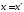болғанда ғана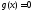

Қателер функциясын ашып жазсақ, онда

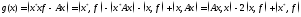
белгісіз болғандықтан 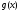-ты есептеу мүмкін болмағандықтан, оның

орнына одан айырмашылығы тұрақты сан болатын

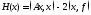(3.3)

функционалын қарастырамыз.

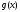пен 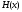-тың айырмашылығы тұрақты сан болғандықтан

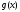-тың азаюын 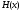-функциясын есептеу арқылы анықтауға болады.

Айталық, 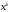-( 3.1) жүйесінің жуық шешуі болсын. Ал жүйені шешу үшін мына

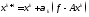(3.4)

итерациялық əдісті қолданайық, ал 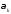итерациялық параметрін

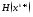-функционалына минимум беретіндей етіп аламыз. Егер 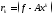десек, онда

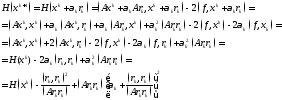
болғандықтан, өзінің минимумына

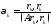(3.5)

болғанда ие болады.

Сонымен итерациялық əдісті былай жазамыз:

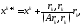
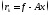(3.6)

Бұл жағдайда

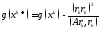(3.7)

Енді осы итерациялық əдістің жинақталу жылдамдығын қарастырайық.

2.1-теорема. Егер 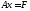жүйесінің матрицасы А оң анықталған жəне

симметриялы болса, онда (3.6) итерациялық əдіс үшін

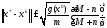
теңсіздігі орындалады. Мұндағы m, M кезегімен А матрицасының ең кіші

жəне ең үлкен меншікті сандары.

Дəлелдеуі. 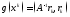болғандықтан (1.7) формуладан

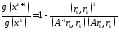(3.8)

формуласын аламыз. Енді 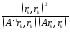өрнегін төменнен бағалайық. Айталық 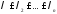А матрицасының меншікті сандары 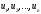ортогональды меншікті векторлары болсын. Яғни,

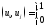
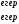
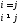
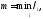
жəне болсын. Енді барлық 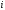-дегі 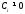саны үшін

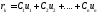
орындалсын. Онда

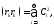
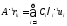
болғандықтан

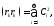
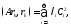v

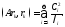
Осыдан

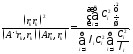(3.9)

Енді 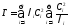өрнегін жоғарыдан бағалайық. Егер  өрнегін тек

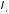-ден тəуелді деп, ал басқа параметрлер түрақты десек, онда оны мына түрде жазуға болады

мұнда

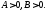
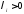болғандықтан 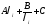функциясының 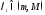аралығында максимумы жоқ. Сондықтан Г өзінің ең үлкен мəніне кейбір m -ге, ал кейбіреуі М-ге тең болғанда ие болады. Яғни, M

i , егер жəне i ,

i k  n1, , 

егер болсын.

k n

2 2

S C S Енді C   ,   десек, онда

1 i 2 i

i1 ik 1

S1 S 2  2 2 m M 

       

S m S M  S S S S

1 2   1 2   1 2

m M  M m 

2 M m 2 2  M m 2 

 S S  S S  S S 1 .

 1 2  1 2  1 2 

Mm  4Mm 

S1 S2  2

S S 

Себебі .

1 2

4

Жəне

M m 2 1 m M  1  m M 2

1 4Mm 4 M 2 m 4  M  m 

болғандықтан

 m M 2

2  M  m  1  m M 2 n 2

        C . (8.10)

S1 S2 4 4  M m   i

  i 1

(8.10) теңдігін ескере отырып (8.9) теңдігінен

2

r , r

  4

k k

1  2 (8.11)

A r ,r Ar ,r   

k k k k M m

  

 m M 

теңсіздігін аламыз.

Енді (8.11) теңсіздігін ескерсек, онда

202

----------------------- Page 203-----------------------

k 1 2

g x   4 M m  

 1  1,

k 2 2

g x    M m M m  

  

 m M 

яғни

2

M m  

k 1 k

g x   g x   немесе

 

M m  

2 1 

k 

M m  

k 1 0

g x    g x   . (8.12)

M m  

g xk  Ay , y m y , y

Ал    k k   k k  болғандықтан

0 k

 

* k g x M m  

x  x   . (8.13)

mM m  

Теорема дəлелденді.

k

M m   k *

Сонымен lim   0 болғандықтан, xlim x  болатынын, яғни ите-



M m  k

k   

рациялық əдістің жинақталатынын көреміз.

Бұл итерациялық əдісті “жылдам түсу əдісі” деп атайды. Оның геометрия-

k k * 1 

x   x A F 

лық мағынасы мынада: Əр H x const 

үшін жəне олар центрі

болатын n-өлшемді эллипсоидтар құрайды.

k k k

r F Ax   x

H x const 

Ал k векторы эллипсоидының нүктедегі нормалі.

1-суретте n 2 болғандағы итерациялық əдістің жинақталу бағыты көр-

сетілген.

Егер А оң анықталмаған немесе симметриялы болмаса, онда (8.1) жүйесін

'

A - түйіндес матрицаға көбейту арқылы

1-сурет

A A'

A ' Ax A 'F жүйесін аламыз. Мұндағы - оң анықталған жəне симме-

триялы болғандықтан бұл жүйеге жылдам түсу əдісін қолдануға болады. Яғни,

итерациялық əдіс мына түрде жазылады:

203

----------------------- Page 204-----------------------

x k 1 x k  A ' F Ax k (8.14)

k  

 

  ,

k k

мұндағы   ,  Ar ' .

k  k k

A ,

k k

x A y  ' AA ' y F

Егер десек, онда болғандықтан

k 1 k k (8.15)

ûûû   ,    

k k k

итерациясын аламыз.

r , r r , r

   

Мұнда   k k  k k .

k

AA 'r ,r  A 'r , A 'r 

k k k k

Ал Ax F жүйесінің шешуі

k k 1 (8.16)

x x A r   '

k k

формуласы арқылы табылады. Бұл əдіс “минимал қателер” немесе Фридман

əдісі деп аталады.

Ескерту. (8.14) формуланы итерациялық əдісті артығымен анықталған

жүйені, ал (8.16) формуланы жартылай анықталған жүйелерді шешуге қол-

дануға болады.

Енді жоғарыдағы қарастырылған (8.6) формуласы бойынша мына теңдеу-

лер жүйесін шешейік:

2 x 3x 

1  2



x13 x2 4



0 T 0 T

  

Бастапқы x 0,0 десек, онда r  F Ax  3, 4 . -ді табу үшін

0     0

ûûû, , , , табайық.

   

0 0 0 0 0

T

2 1 

; , , 90, , 25

Ar   Ar r  r r 

   

0   0 0 0 0

9 6 

25

сондықтан   0, 2778 , яғни

0

90

 1

x

0 0,2778 3 0,8333

1



1

 .

x

0 0,2778 4 1,1112

2

Енді келесі жуықтауды табайық:

r , r

T  

T 1 1

, Ar  0,2775; 0, 2785 , осыдан   0,7144 .

   

0,2222r; 0,1669 1 1

1

Ar ,r 

1 1

 2

x

0,8333 0,7144 0,2222 0,9920

1



2

 .

x

1,1112 0,7144 0,1669 2 0,9920



Тағы сол сияқты итерация берілген дəлдікке жеткенше жалғаса береді.

204

----------------------- Page 205-----------------------

8.2. Толық емес релаксациялық градиентті əдіс

Айталық, Ax  f теңдеулер жүйесінде А оң анықталған симметриялы ма-

трица болсын. Жүйені шешу үшін

x x k r k1  k k (8.17)

итерациялық əдісін қолданайы қ. Мұнда

r , r

 

q , k k (8.18)

    

k k k k

Ar ,r 

k k

болсын.

Сонда

k +1 k q q2 k

g x =g x -2 r ,r + Ar ,r =g x -

( ) ( ) ( ) ( ) ( )

k k k k k k

2

r , r

( )

2 2 k k k

2q a r , r +q a Ar , r =g x -2q + (8.19)

( ) ( ) ( )

k k k k k k k k k

(Ar ,r )

k k

2 2

r , r r , r

( ) ( )

+q2 k k =g xk - 2q -q2 k k .

k ( ) ( k k )

(Ar ,r ) (Ar ,r )

k k k k

k 1 k

   

g x g x 

Осы теңдіктен теңсіздігі орындалуы үшін

0  2 qk (8.20)

шарты орындалуы жеткілікті.

Егер qk 1, бірақ барлық q k бірге тең болмаса, онда итерациялық əдісті

төменгі релаксациялық, ал qk 1, бірақ барлық q k бірге тең болмаса, онда

итерациялық əдісті жоғарғы релаксациялық əдіс дейді.

Егер

2

 0 q

   жəне k (8.21)

k

M

теңсіздігі орындалса, онда (8.17) итерациялық əдісті толық емес градиенттік

итерациялық əдіске жатқызуға болады. Мұнда М – А матрицасының ең үлкен

мешікті саны.

Шынында да бұл жағдайда

q Ar ,r

q ( k k )

0 <qk = = £q⋅M <2

a r , r

( )

k k k

f (x ) функциясы əр қадам сайын кеміп отыруы үшін (8.21) шарты қажетті

де. Себебі

q (Ar ,r )

0 <q = =q k k <2

k

a r , r

( )

k k k

205

----------------------- Page 206-----------------------

теңсіздігінен

(2r , r )

0 <q< k k

(Ar ,r )

k k

теңсіздігін аламыз жəне бұл теңсіздік барлық rk үшін орындалатындықтан

2 z, z

( ) 2

0 <q<min =

(Az ,z ) M

теңсіздігі орындалады.

Яғни, толық емес градиенттік əдіс const болғанда алдын ала мына

түрге

x E Ax f  

келтірілген теңдеулер жүйесін біртіндеп жуықтау əдісімен шешкенмен пара-

пар.

Жəне

k 1   k

x E  Ax f  (8.22)

итерациялық процесі жинақталу үшін

2

 0 qk

M

шарты орындалуы қажетті жəне жеткілікті.

E A 

Жалпы теория бойынша (8.22) итерациялық əдісі қаншалықты бірден

кіші болса, соншалықты жылдам жинақталады. Ондай мақсатқа жеткізетін 

мына минимакс есебінің

minEmaxA1  ( )  A (8.23)

i

 i

шешімі болатыны анық.

Бұл есептің шешуін

 1m 1 M 

теңдеуінен табамыз:

2

 . (8.24)

m M

M m 

Сондықтан

E A 

M m 

k

k M m  

* 0 *

x  x  x x 

болғандықтан,   теңсіздігі орындалады.

M m  

Енді (8.17) əдісі үшін жалпы жинақталу теоремасын дəлелдейік.

8.2-теорема. Егер А – оң анықталған симметриялы матрица жəне

   2 , 0q 1  болса, онда

k

206

----------------------- Page 207-----------------------

0

k ( )

* 1 k  g x

, (8.25)

  

x x

1

m

2

2 æçM -m ö÷

мұнда t =1- 2e-e 1-t , t= .

1 ( )( ) çç ÷÷

èM +m ø

k

Дəлелдеуі. Айталық x - толық емес релаксациялық əдіс арқылы алынған

k 1

_

k

(8.1) жүйесінің жуық шешуі болсын. Ал x жүйенің x жуық шешуін

қолдану арқылы жылдам түсу əдісімен табылған жүйенің жуық шешуі болсын.

k 1 k 1

  k k     k

g x g x    g x f x     1 g x  

Онда   болғандықтан,   .

   

2

r , r

( )

k +1 k 2 k k

= - -

Жəне g x g x 2q q болғандықтан

( ) ( ) ( k k )

(Ar ,r )

k k

2

-k +1 é -k +1 ù

æ ö æ ö

r , r

( )

ç ÷÷ k 2 k k 2 ê k ç ÷÷ú

g x g x 2q q 2q q g x g x .

ç £ - - = - - ç

çç ÷÷ ( ) ( k k ) ( k k ) ( )ê çç ÷÷ú

è ø (Ar ,r ) ê è øú

k k ë û

2

k +1

-

æ ö

r , r

( )

Енді g xk -g ççx ÷÷= k k екенін ескерсек, онда

( ) çç ÷÷

è ø (Ar ,r )

k k

g xk -g xk +1 ³ 2q -q 2 1-t g xk

( ) ( ) ( k k )( ) ( ).

Сондықтан

k +1 é 2 ù k é 2 ù k

£ - - - £ - - -

g x 1 2q q 1 t g x 1 2e e 1 t g x ,

( ) êë ( k k )( )úû ( ) êë ( )( )úû ( )

k

k +1 é 2 ù 0

немесе £ - - - .

g x 1 2e e 1 t g x

( ) êë ( )( )úû ( )

k +1 2

g x = Ay , y ³m y

Енді ( ) ( k +1 k +1 ) k +1 екенін ескерсек

0

k g (x )

y k + £( )t .

1 1

m

Теорема дəлелденді.

8.3. Минимал ауытқу əдісі

Айталық, Ax =F теңдеулер жүйесі берілсін жəне A 0 болсын. Жүйені

шешу үшін

x k +1 =x k +t F -Ax k (8.26)

k ( )

итерациялық əдісін қолданайық. k параметрін былайша аламыз:

(8.26) теңдігін А матрицасына көбейтіп, теңдіктің екі жағын да F векторы-

нан алып тастайық, сонда

207

----------------------- Page 208-----------------------

r =r -t Ar (8.27)

k +1 k k k

k

теңдігін аламыз. Мұнда r =F -Ax .

k

Осыдан

2

r , r = r , r -2t Ar , r +t Ar , r =

( ) ( ) ( ) ( )

k + k + k k k k k k k k

1 1

Ar ,r 2 é Ar ,r ù2

( k k ) ê ( k k )ú

= r , r - + Ar , Ar t - (8.28)

( ) ( )

k k k k ê k ú

(Ar , Ar ) ê (Ar , Ar )ú

k k ë k k û

r r , 

болғандықтан өзінің минимал мəніне

k 1 k 1

(Ar ,r )

t = k k (8.29)

k

(Ar , Ar )

k k

болғанда ие болады. Яғни, (8.26) итерациялық процесін былай жазамыз:

(Ar ,r )

k +1 k k k . (8.30)

= + ⋅

x x r

k

(Ar , Ar )

k k

Ал (8.29) теңдігін ескерсек, онда (8.28) теңдіктен

é 2 ù

(Ar ,r )

ê k k ú

= - (8.31)

r , r 1 r , r

( ) ( )

k +1 k +1 ê ú k k

Ar , Ar r ,r

ê ( )( )ú

ë k k k k û

теңдігін аламыз.

2

(Ar ,r )

Енді g =1- k k 0  1 g

k өрнегінің k екенін көрсетейік. Ол үшін

Ar , Ar r ,r

( )( )

k k k k

Коши-Буняковский теңсіздігін пайдаланамыз:

2 2 2

(Ar ,r ) £ Ar ⋅r .

k k k k

2

(Ar ,r )

2 k k 2

Демек r = <1 болғандықтан . Сонымен бірге 

k 0  1 g k k

Ar , Ar r ,r

( )( )

k k k k

нөлге жинақталмайды, себебі

æ ö (Ar ,r ) ì æ öü

A +A ' k k ï A +A ' ï

(Ar ,r )=çç r ,r ÷÷ жəне inf =min íïl çç ÷÷ýï.

k k ç k k ÷ s ç ÷

r s ï è øï

è ø k r , r 2

2 ( )

k k ï ï

î þ

g 1 r r  lim 0 r 

Осыдан k болғандықтан , яғни k . Сонымен, егер

k k 1

k 

(Ar ,r )

k k

t =

k

(Ar , Ar )

k k

208

----------------------- Page 209-----------------------

болса, онда (8.26) итерациялық əдісі кез келген Ax =F ( A 0 ) жүйесі үшін

жинақталатындығын көреміз.

Егер А оң анықталған симметриялы матрица болса, онда

2

t (Ar ,r )

k k k

qk = = £1

a Ar , Ar r ,r

( )( )

k k k k k

болғандықтан ( матрицасының меншікті векторы болғанда ғана q 1

r A , k

k

болады) минимал ауытқу əдісін төменгі релаксациялық градиентті əдіске

жатқызуға болады. Сондықтан 8.2-теореманың шартын қанағаттандыратын-

дықтан (8.25) теңсіздігі орындалады.

Минимал ауытқу əдісінің басқа итерациялық əдістерге қарағанда артықшы-

лығы оның кез келген A 0 жүйе үшін жинақталатындығы.

Сұрақтар мен тапсырмалар

Ax =F теңдеулер жүйесін шешу үшін жылдам түсу əдісін қай уақытта

қолдануға болады?

g

  кесіндісінде анықталған dx + +f өрнегі өзінің ең үлкен мəніне

a b,

x

x a  x b 

немесе болғанда ие болатындығын дəлелде.

А – оң анықталған матрица. Ax =F , A 'Ax =A 'F жүйелерін жылдам

түсу əдісімен шешкен кезде қай жүйе үшін итерациялық əдіс жылдам жинақ-

талатынын анықта.

q =min max {1-ta, 1-tb} өрнегінің шешуі 1-ta=- 1-tb( ) болғанда табы

t

латынын дəлелде.

А – оң анықталмаған болса, онда Ax =F жүйесін жылдам түсу əдісімен

қалай шешуге болады?

А симметриялы оң анықталған матрица. Минимал ауытқу əдісі үшін

k

k MM m  

* 0 *

x  x   x  x  теңсіздігін алуға болатындығын дəлелдеңіз.

Mm m  

Минимал ауытқу əдісін қандай жағдайларда қолданған тиімді?

Зертханалық жұмыстар

1-тапсырма. 8-параграфта көрсетілген əдістерге бағдарлама құрыңыздар.

2-тапсырма. 6-параграфтағы Зертханалық жұмыстарда көрсетілген теңдеу-

лер жүйесін градиентті итерациялық əдіс арқылы шешіңіздер.

209

----------------------- Page 210-----------------------