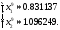Теңдеулер жүйесін қарапайым итерациялық əдістермен

шешу жолдары.

1. Итерациялық процестерді құру принципі

Көп жағдайда теңдеулер жүйесін дəл əдіске қарағанда итерациялық əдіспен

шешкен тиімдірек. Себебі:

1. Егер итерациялық процесс жылдам жинақталатын болса, онда теңдеулер

жүйесін шешуге жіберілген арифметикалық амалдар саны мен оны есептеуге

жіберілген уақыт үнемделеді.

2. Итерациялық əдіс өзін-өзі түзетіп отыратындықтан, есептеу кезінде жібе-

рілген қателер жалпы теңдеулер жүйесінің шешуіне əсерін тигізбейді.

3. Итерация əдісінің алгоритмі онша күрделі болмағандықтан, ЭЕМ-ға бағ-

дарлама оңай құрылады.

4. Теңдеулер жүйесінің матрицасының элементтерінің көпшілігі нөлге тең

болған жағдайда итерация əдісінің тиімділігі арта түседі.

Енді осы итерациялық процесті құру схемасымен танысайық.

Айталық,

AX=F (1.1)

теңдеулер жүйесі берілсін жəне 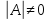делік. Осы теңдеулер жүйесін шешу

үшін

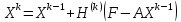(1.2)

формуласы бойынша 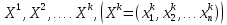– итерацияның k-қадам-

дағы жуықтауы векторлар тізбегін табамыз. 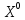– бастапқы кез келген вектор,

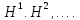матрицалар тізбегі. (1.2)-формуласын итерациялық əдіс дейміз.

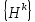матрицалар тізбегінің түріне қарай (1.2)-формуласынан əртүрлі

итерациялық процестерді аламыз. Егер 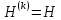, яғниk -дан тəуелсіз болса,

онда итерациялық процесті “стационар”, ал 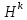k -дан тəуелді болса

“ста ционар емес” деп, ал 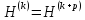болса, онда p қадамды итерациялық про-

цесс дейміз. Итерациялық процестер үшін (1.1) теңдеулер жүйесінің шешуі қозғал-

майтын нүкте болып табылады, яғни 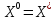деп алсақ, онда (1.2) формула

бойынша тапқан келесі векторымыз да болады.

Керісінше 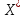қозғалмайтын нүкте болатын кез келген мынадай итерация-

лық процесті

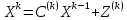(1.3)

мұнда 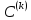– матрицалар тізбегі,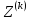– векторлар тізбегі, (1.2) түрінде жазуға болады.

Шынында да 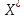үшін

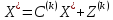
Болғандықтан

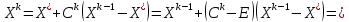
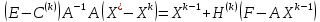
мұнда .

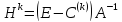Енді итерациялық процестің жинақталуын қарастыру үшін (1.2) теңдігін

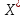векторынан алып тастайық, яғни

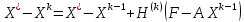(1.4)

Осы формуланы былайша жазсақ

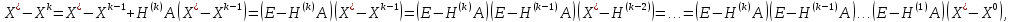
онда 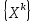-векторлар тізбегінің 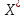векторына жинақталуы үшін

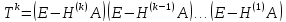
матрицасының нөлге ұмтылуы қажетті жəне жеткілікті, ал 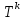матрицасының кез келген нормасының нөлге ұмтылуы жеткілікті шарт екенін көреміз.

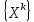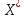Ал векторлар тізбегінің векторына ұмтылу жылдамдығы 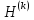матрицасына байланысты болғандықтан, оны таңдау əртүрлі итерациялық əдістерге əкеледі.

Енді итерациялық əдістердің жинақтылығын қалай сипаттауға болады, немесе қай уақытта итерациялық процесті тоқтату керектігіне тоқталайық. Теңдеулер жүйесінің дәлдігін 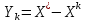қателік векторы арқылы бағалау мүмкін болмағандықтан көбіне 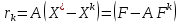-ауытқу векторы арқылы бағалайды. Шынында да, егер 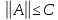(C-const) болса, онда

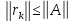
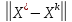
Осыдан 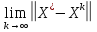=0 болғанда 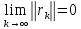екенін көреміз. Ал

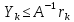(1.6)

болғандықтан

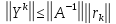
Осыдан мынадай тұжырым жасауға болады: Егер (C-const), яғни (1.1) орнықты болса, онда 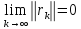шегінен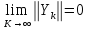шегі келіп шығады. АлA матрицасының шарттылығы нашар болған жағдайда бұл тұжырым орындалмауы да мүмкін.

Мысалы:

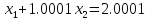
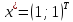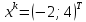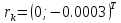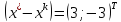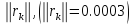теңдеулер жүйесінің дəл шешуі .Егер деп алсақ, онда болады, ал. Осыдан ауытқу векторыныңнормасы аз шама болғанымен, қателік векторының нормасы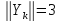 екенін көреміз.

Сондықтан итерациялық процесті алдын ала берілген дəлдік 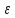бойынша 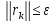теңсіздігі орындалған кезде тоқтату ертерек болуы мүмкін. Енді (1.4) теңдігін былайша жазайық:

.

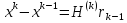Осыдан

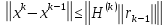
Бұл теңсіздік, (1.1) теңдеулер жүйесі орнықты болған жағдайда, итерациялық процесті

(1.7)

теңсіздігі орындалғанда тоқтатуға болатындығын көрсетеді.

Егер А оң анықталған симметриялы матрица болған жағдайда қателік вектордың шамасын қателік функциясы деп аталатын

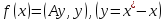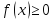функцияның шамасымен де анықтауға болады. Шынында да, А оң анықталған болғандықтан, жəне 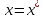болғанда.

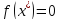Сонымен қатар

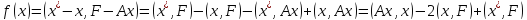
болғандықтан, оның мəнін табу мүмкін емес. Бірақ

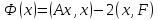(6.8)

функционалының қателік функциясынан айырмашылығы тұрақты сан болғандықтан жəне екеуі де өздерінің ең кіші мəндеріне 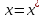болғанда ие болатындығын ескерсек, Ф(х) функционалына минимум мəн беретін векторды жүйенің шешуі деп қарастыруға болады. Сондықтан

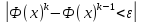(1.9)

болған жағдайда да итерациялық процесті тоқтатуға болады.

Енді итерациялық процестердің қарапайым түрлерімен танысайық.

1.2. Біртіндеп жуықтау əдісі

Берілген

Ax=F

теңдеулер жүйесін былайша жазайық

x=Bx+F (1.10)

мұнда B=E-A.

Енді (1.10) теңдеулер жүйесін шешу үшін мынадай итерациялық əдісті пайдаланайық

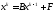(1.11)

мұнда 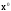– өзіміздің еркіміз бойынша алынатын кез келген бастапқы вектор. (1.11) итерациялық əдісін (612) формуласы түрінде жазсақ

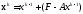
онда 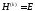екенін жəне бұл стационар итерациялық əдіс екенін көреміз.

Бұл əдістің жинақтылығын анықтау үшін математикалық индукцияны қолдану арқылы, (1.11) теңдігінен алынған

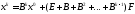(1.12)

жəне 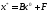теңдігінен (1.11) теңдігін алып тастағанда алынған

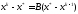(1.13)

формуланы қарастырайық.

Енді осы формуланы қолдана отырып, əдістің жинақтылығы туралы бірнеше теоремаларды дəлелдейік.

1.1-теорема: Кез келген 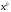-де біртіндеп жуықтау əдісінің жинақты болуы үшін B матрицасының меншікті мəндерінің модулі бірден кіші болуы қажетті жəне жеткілікті.

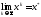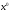Дəлелдеуі. Айталық, . Онда кез келгенүшін

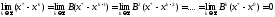
болғандықтан,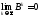. Себебі .

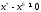Сондықтан 2.2-теорема бойынша B матрицасының меншікті мəндерінің модулі бірден кіші.

Енді B матрицасының меншікті мəндерінің модулі бірден кіші болсын, онда

2.2-теорема бойынша 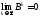жəне

2.5-теорема бойынша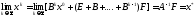

Теорема дəлелденді.

Бұл теореманың шартын тексеру қиын болғандықтан, шарттары оңай анықталатын теоремаларды қарастырайық.

6.2-теорема: Біртіндеп жуықтау əдісі жинақталуы үшін 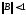болуы жеткілікті.

Дəлелдеуі. 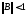болғандықтан 2.3-теорема бойынша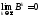Онда 2.2-теорема бойынша B матрицасының меншікті мəндерінің модулдері бірден кіші. Сондықтан 1.1-теореманың шарты орындалады, яғни біртіндеп жуықтау əдісі жинақталады. Теорема дəлелденді.

Əдістің жинақталу жылдамдығын келесі теорема арқылы анықтауға болады:

6.3-теорема: Егер 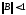болса, онда

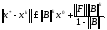(1.14)

Дəлелдеуі. 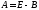болғандықтан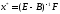. Осы теңдіктен (1.12) теңдігін алсақ, онда

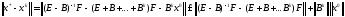
Енді осы теңсіздікке 2.6-теореманы қолдансақ, онда

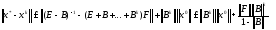
Теорема дəлелденді.

Көп жағдайда 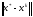жəне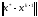нормаларын салыстыруға тура кeледі. Бұл сұраққа келесі теорема жауап береді.

6.4-теорема: 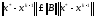(1.15)

Дəлелдеуі. (1.13) теңдіктен

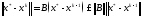
Теорема дəлелденді.

Сонымен қоса 1.4-теореманы пайдалану арқылы мынадай бағалауды алуға болады.

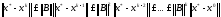
яғни 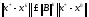(1.16)

(6.14), (6.16) теңсіздіктеріне сүйенсек, онда біртіндеп жуықтау əдісінің

келесі шарттар орындалғанда жинақталатынын көреміз.

1. Егер 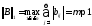болса, онда əдіс жинақталады жəне

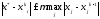теңсіздігі орындалады. Мұнда

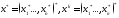
2. 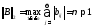болған жағдайда əдіс жинақталады жəне

3. болса, онда əдіс жинақталады жəне

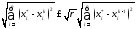теңсіздігі орындалады.

Сонымен берілген жүйесін біртіндеп жуықтау əдісімен шешу үшін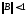немесе оның меншікті санының модулі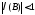болатындай етіп алдын ала түрлендіріп алу керек.

Ондай түрлендірудің бір жолы мынадай:

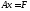жүйесін солдан түйіндес матрицаға көбейтеміз

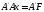(1.17)

Енді (1.17) жүйесін 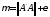(– кез келген теріс емес сан) санына бөліп, оған біртіндеп жуықтау əдісін қолдансақ, онда

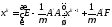(1.18)

итерациялық процесіндегі 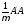матрицасының меншікті саны

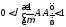(1.19)

болғандықтан 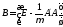матрицасының меншікті саны үшін мына теңсіздік орындалады:

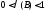
Сондықтан 6.1-теореманың шарты бойынша (6.18) итерациялық əдіс жи- нақталады.

Мысалы:

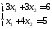(1.20)

теңдеулер жүйесі берілсін.

Мұнда 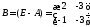болғандықтан

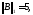
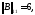
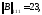ал

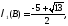
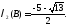
B матрицасының біз қарастырған нормалары мен ең үлкен меншікті саны- ның модулі бірден үлкен болғандықтан

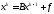
итерациялық əдіс жинақталмайды.

Енді (1.20) жүйесін 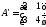матрицасына сол жақтан көбейтсек

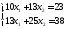(1.21)

жүйесін аламыз.

Мұндағы болғандықтан, (1.21) теңдеулер жүйесін 40-қа

бөлеміз 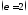. Сонда.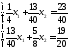

Осыдан 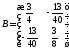болғандықтан 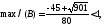яғни

1.1-теореманың шарты орындалады. Сондықтан

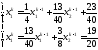
итерациялық процесі жинақты.

Енді осы итерациялық процесті шешейік.

Айталық ,

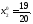
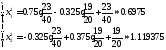
тағы сол сияқты