Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Государственный Университет Управления

Институт инноватики и логистики

Кафедра прикладной математики

Курсовая работа

По дисциплине: «Прикладная математика»

Выполнил	Жамалетдинов Руслан Халитович
Институт	ИИиЛ
Специальность	Логистика
Специализация
Вариант	4
Курс	II
Группа	2
Руководитель	Чистяков Владимир Сергеевич
Дата сдачи на проверку
Дата защиты
Оценка
Подпись руководителя

Москва 2006

Содержание:

Задача о «расшивке узких мест производства» 6

1. Линейная производственная задача

Предприятие выпускает 4 вида продукции, используя 3 вида ресурсов.

Технологическая матрица производства (A), запас ресурсов (B), удельная прибыль предприятия от производства и реализации каждого вида продукции (C) известны.

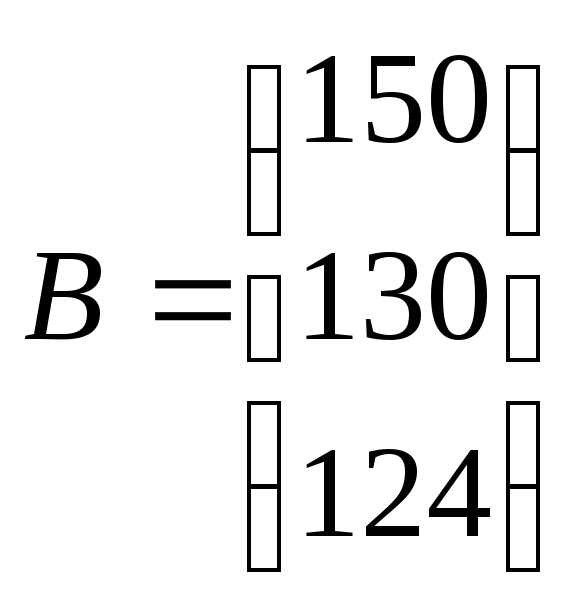
Требуется составить такой план производства продукции X=(x₁,x₂,x₃,x₄), реализация которого обеспечивает предприятие наибольшей прибылью.

При производстве x₁ – единиц продукции Первого вида, x₂ – единиц продукции Второго вида, x₃ – единиц продукции Третьего вида, x₄ – единиц продукции Четвёртого вида предприятие затрачивает 3x₁+2x₂+6x₃+0x₄ единиц ресурсов Первого вида.

Очевидно, что оно не должно превышать имеющийся запас ресурса Первого вида, а именно 150.

Составив аналогичные ограничения для ресурсов Второго и Третьего видов, получаем систему неравенств:

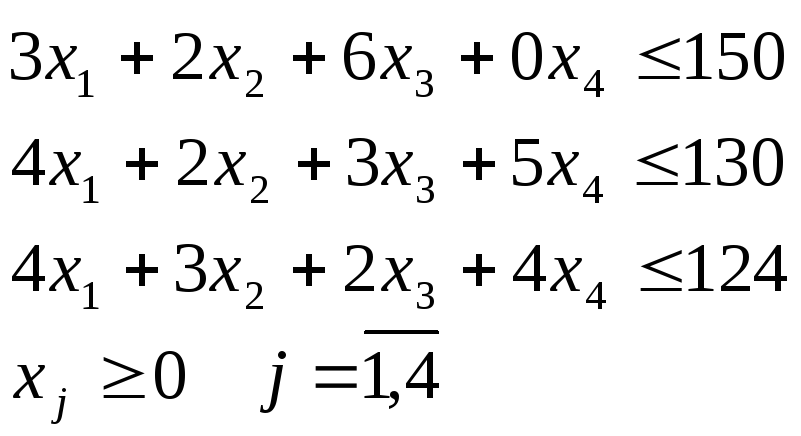
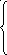(1)

Z=30x₁+11x₂+45x₃+6x₄

В качестве критерия эффективности правомерно принять принцип максимального результата, поэтому математическая постановка задачи выглядит следующим образом: найти вектор X, обеспечивающий максимум линейной форме Z=30x₁+11x₂+45x₃+6x₄ при ограничивающих неравенствах (1) на его компоненты.

Данная задача является задачей линейного программирования. Для её решения симплексным методом проведём систему ограничений к предпочтительному виду за счёт введения в левую часть каждого ограничения по одной дополнительной неотрицательной неизвестной x₅, x₆, x₇.

Переменные x₅, x₆, x₇ по экономическому смыслу будут представлять собой остаток ресурсов Первого, Второго и Третьего видов соответственно.

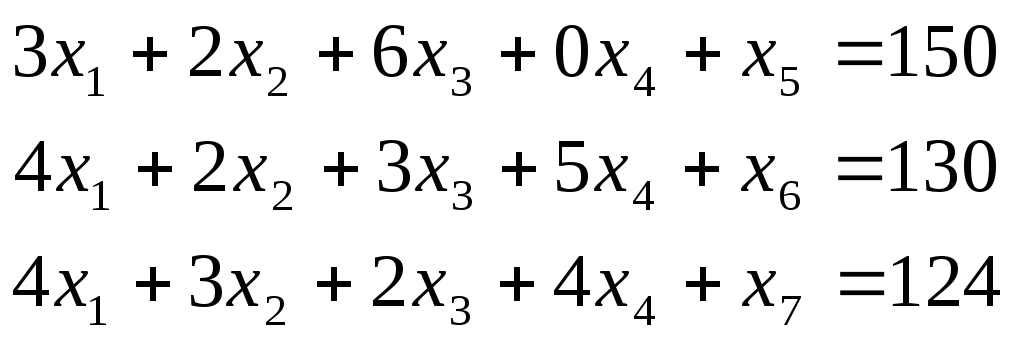
Выразим функцию Z таким образом для подстановки в таблицу:

0-Z=-30x₁-11x₂-45x₃-6x₄

Решим систему симплексным методом:

C	Базис	H	х1	х2	х3	х4	х5	х6	х7	Примечание
0	Х5	150	3	2	6	0	1	0	0	Min ∆j=-45 х3 – в базис min(H/ai3>0)= =min(150/6;130/3;124/2)=150/6=25 х5 – из базиса 1-е ур-ие разрешающее
0	Х6	130	4	2	3	5	0	1	0
0	Х7	124	4	3	2	4	0	0	1
		0-Z	-30	-11	-45	-6	0	0	0
										Min ∆j=-15/2 х1 – в базис min(50;22;74/3)=22 х6 – из базиса 2-е ур-ие разрешающее
45	X3	25	1/2	1/3	1	0	1/6	0	0
0	Х6	55	5/2	1	0	5	-1/2	1	0
0	Х7	74	3	7/3	0	4	-1/3	0	1
		1125-Z	-15/2	4	0	-6	15/2	0	0
										Все ∆j=>0 => решение оптимальное X=(22;0;14;0;0;0;8) Zmax=1290
45	Х3	14	0	2/15	1	-1	4/15	-1/5	0
30	Х1	22	1	2/5	0	2	-1/5	2/5	0
0	Х7	8	0	17/15	0	-2	4/15	-6/5	1
		1290-Z	0	7	0	9	6	3	0

Оптимальная производственная программа: x₁=22, x₂=0, x₃=14, x₄=0.

Остатки ресурсов: первого вида –x₅=0, второго вида –x₆=0, третьего вида – x₇=8.

Узкими местами производства, т.е. ресурсами, использующимися полностью, являются 1-й и 2-й ресурсы, x₅=0 и x₆=0 соответственно.

Среди коэффициентов при неизвестных в левой части уравнения нет ни одного отрицательного. Если из этого уравнения выразить функцию цели z через остальные неотрицательные переменные

z = 1290 - 7х₂ - 9х₄ - 6х₅ - 3х₆ (2)

то становится совершенно очевидным (в силу того, что все x_j0), что прибыль будет наибольшей тогда, когда x₂=0, x₄=0, x₅=0, x₆=0

Это означает, что производственная программа (2) является наилучшей и обеспечивает предприятию наибольшую прибыль z_max = 1290

Обращенный базис, отвечающий оптимальной производственной программе, содержится в последней симплексной таблице:

Для того, чтобы убедиться в правильности полученного решения, следует проверить отношение Н = Q^-1 * В:

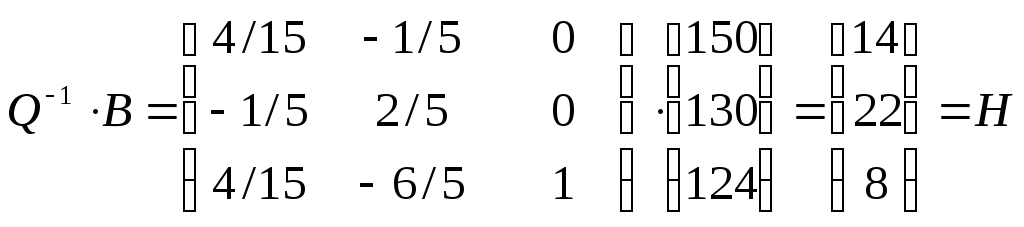
Воспользуемся тем, что в оптимальной производственной программе х₂=0, х₄=0. Предположим, что продукции Второго и Четвёртого видов мы не намеревались выпускать с самого начала. Рассмотрим задачу с оставшимися двумя переменными, сохранив их нумерацию. Математическая модель задачи будет выглядеть следующим образом:

F(x₁,x₃)=30x₁+45x₃→max

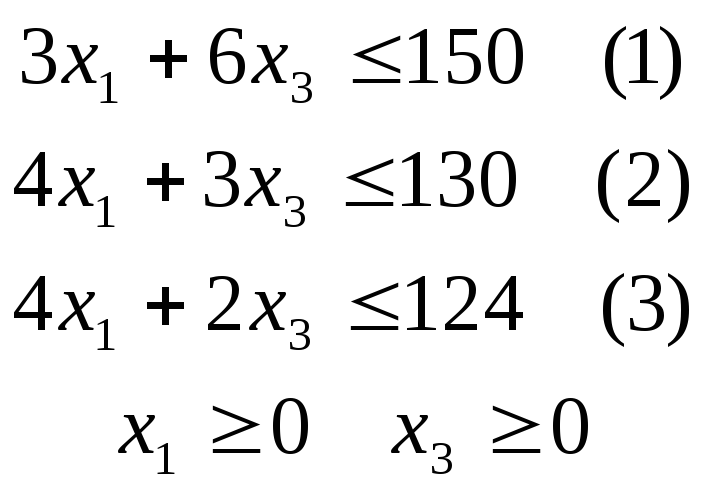
- направления наибольшего роста целевой функции F.

В точке А достигается максимальное значение функции F. Найдём её координаты:

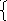
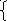
F(22;14)=F_max=30*22+45*14=1290