Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Государственный Университет Управления

Кафедра Прикладной математике

Курсовая работа

по дисциплине: «Прикладная математика»

Вариант №1

Выполнила _________________________________Аксенова Е.И.

Институт ______________________________________ ИУХМП

Специальность _______________________ Менеджмент организации

Специализация ________________________________________МБХТ

Отделение _____________________________вечернее отделение

Курс ____________________________________________ II

Группа _____________________________________________1

Руководитель _____________________________ Супоницкий В. Л.

Дата сдачи на проверку _____________________________________14.12.05г.

Дата защиты _____________________________________________

Оценка _____________________________________________

Подпись руководителя _____________________________________________

г. Москва

2005Г. Содержание курсовой работы

Задание на курсовую работу 3

1. Линейная задача производственного планирования 6

2. Двойственная задача линейного программирования 11

Задача о «расшивке узких мест» 12

3. Транспортная задача линейного программирования 15

4. Динамическое программирование 18

5. Матричная игра как модель конкуренции и сотрудничества 21

6. Матричная модель производственной программы 24

7. Анализ доходности и рискованности финансовых опера­ций 27

Литература 30

Задание на курсовую работу.

1. Сформулировать линейную производственную задачу и составить её математическую модель, имея следующие исходные данные:

Преобразовать данную задачу к виду основной задачи линейного программирования, решить её методом направленного перебора базисных допустимых решений, обосновывая каждый шаг процесса, найти оптимальную производственную программу, максимальную прибыль, остатки ресурсов различных видов и указать «узкие места» производства.

В последней симплексной таблице указать обращённый базис соответствующий оптимальному набору базисных неизвестных. Проверить выполнение соотношения.

Если по оптимальной производственной программе какие-то два вида продукции не должны выпускаться, то в таблице исходных данных вычеркнуть соответствующие два столбца, составить математическую модель задачи оптимизации производственной программы с двумя оставшимися переменными, сохранив прежнюю нумерацию переменных и решить графически.

2. Сформулировать задачу, двойственную линейной производственной задаче, как задачу определения расчётных оценок ресурсов, и найти её решение, пользуясь второй основной теоремой двойственности (о дополняющей нежёсткости). Указать оценку единицы каждого ресурса, минимальную суммарную оценку всех ресурсов, оценку технологий.

Применить наёденные двойственные оценки ресурсов к решению следующей задачи.

Сформулировать задачу о «расшивке узких мест производства» и составить математическую модель. Определить область устойчивости двойственных оценок, где сохраняется структура программы производства. Решить задачу о «расшивке узких мест производства» при условии, что дополнительно можно получить от поставщиков не более одной трети первоначально выделенного объёма ресурса любого вида (если задача окажется с двумя переменными, то только графически); найти план приобретения дополнительных объёмов ресурсов, дополнительную возможную прибыль.

Составить сводку результатов.

3. Составить математическую модель транспортной задачи по следующим данным:

Вектор объёма производства

Вектор объёма потребления

Матрица транспортных издержек:

Если полученная модель окажется открытой, то свести её к замкнутой и найти оптимальное решение транспортной задачи методом потенциалов.

4. Методом динамического программирования решить задачу распределения капитальных вложений между четырьмя предприятиями производственного объединения, располагающего суммой в 700 тыс. руб., причем выделяемые суммы должны быть кратны 100 тыс. руб. по следующим исходным данным:

хj	0	100	200	300	400	500	600	700
f1	0	20	44	55	63	67	70	70
f2	0	18	29	49	72	87	100	108
f3	0	25	41	52	74	82	88	90
f4	0	30	52	76	90	104	116	125

5. Рассмотреть матричную игру как модель сотрудничества и конкуренции по следующим исходным данным:

Найти графически решение игры. Указать, как проявляется конкуренция между игроками и сотрудничество между ними.

6. Составить матричную модель производственной программы предприятия по следующим исходным данным:

структурная матрица производства А =

матрица коэффициентов прямых затрат (затраты на физический выпуск)

B =

матрица коэффициентов прямых затрат внешних ресурсов Y =

По данному вектору выпуска товарной продукции найти вектор производственной программы и полные затраты всех внешних ресурсов.

7. Провести анализ доходности и риска финансовых операций по следующим исходным данным:

Q1	0	2	4	8		Q2	2	4	6	18
	1/2	1/4	1/8	1/8			1/2	1/4	1/8	1/8
Q3	0	4	6	12		Q4	2	6	8	14
	1/4	1/4	1/3	1/6			1/4	1/4	1/3	1/6

1. Линейная производственная задача.

Предприятие может выпускать п видов продукции, используя т ви­дов ресурсов. Пусть а_ij - расход; i-ого ресурса на единицу j-ой продукции, b_i,- имеющееся количество i-го ресурса, с_j - прибыль на единицу j-й про­дукции, х_j - искомое количество единиц j-й продукции. Задача состоит в том, чтобы найти производственную программу

X = (x_1, x₂, … x_n) максимизирующую прибыль

(1)

при ограничениях по ресурсам

(2)

где по смыслу задачи x_j  0.

Исходные данные задачи моего варианта представлены в виде:

45	60	21	14
3	6	3	0	180
6	2	0	6	210
2	3	5	7	112

т.е. матрица А удельных затрат ресурсов, вектор В объемов ресурсов и век­тор С удельной прибыли имеют вид

А=В =С = (45 60 21 14)

Математическая же модель задачи: найти производственную программу (x_1, x₂, x₃, x₄), максимизирующую прибыль

P(x_1, x₂, x₃, x₄) = 45x₁ + 60х₂ + 21x₃ + 14x₄  max, (4)

при ограничениях по ресурсам

3x₁ + 6х₂ + 3x₃ + 0x₄  180

6x₁ + 2х₂ + 0x₃ + 6x₄  210 (5)

2x₁ + 3х₂ + 5x₃ + 7x₄  112

где по смыслу задачи x₁  0, x₂  0, x₃  0, x₄  0 (6)

Получили задачу линейного программирования. Чтобы решить ее, заменяем неравенства системы (5) уравнениями при помощи до­полнительных неотрицательных неизвестных х₅, х₆, х₇, которые имеют эко­номический смысл остатков ресурсов. Эти переменные называются балансовыми. Получается каноническая задача ЛП максимизировать линейную форму (4) при условиях:

3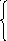x₁ + 6х₂ + 3x₃ + 0x₄ + х₅ + 0х₆ + 0х₇ = 180

6x₁ + 2х₂ + 0x₃ + 6x₄ + 0х₅ + х₆ + 0х₇ = 210 (7)

2x₁ + 3х₂ + 5x₃ + 7x₄ + 0х₅ + 0х₆ + х₇ = 112

гдеx₁  0,

x₂  0,

x₃  0,

x₄  0,

x₅  0,

x₆  0,

x₇  0.

Применим симплексный метод к решению этой задачи. Процесс решения приведен в таблице.

Б	Б	Н	45	60	21	14	0	0	0	Примечания
			Х1	Х2	Х3	Х4	Х5	Х6	Х7
0	Х5	180	3	6	3	0	1	0	0	180 / 6 = 30 min
0	Х6	210	6	2	0	6	0	1	0	210 / 2 = 105
0	Х7	112	2	3	5	7	0	0	1	112 / 3 ≈ 37,3
	Z	0	–45	–60	–21	–14	0	0	0	Z=Б∙H; ∆j=Б∙G-сj;min∆j=–60
60	Х2	30	1/2	1	1/2	0	1/6	0	0	30 / 1/2 = 60
0	Х6	150	5	0	–1	6	–1/3	1	0	150 / 5 = 30 min
0	Х7	22	1/2	0	7/2	7	–1/2	0	1	22 / 1/2 = 44
	Z	1800	–15	0	9	–14	10	0	0	∆j= –15min
60	Х2	15	0	1	3/5	–3/5	1/5	–1/10	0
45	Х1	30	1	0	–1/5	6/5	–1/15	1/5	0
0	Х7	7	0	0	18/5	32/5	–7/15	–1/10	1
	Z	2250	0	0	6	4	9	3	0

Если все оценочные коэффициенты (нижние строки каждой симплексной таблицы) неотрицательны, то получено оптимальное решение: базисные переменные равны свободным членам, остальные равны нулю, максимум целевой функции указан правее буквы Z. Если есть отрицательные оценочные коэффициенты, то находят самый малый из них (в первой таблице это -60). Если в столбце над ним нет положительных элементов, то задача не имеет решения. Если есть, то ищем минимальное отношение свободных членов к разрешающим элементам указанного столбца. В пересечении строки с минимальным показателем и столбца с минимальным оценочным коэффициентом получаем разрешающий элемент.

Так как все оценочные коэффициенты неотрицательны, то получено оптимальное решение: базисные переменные равны свободным членам, остальные равны нулю, максимум целевой функции указан правее буквы Z. Таким образом, имеем решение:

Производственная программа x₁= 30, x₂= 15, x₇= 7, является оптимальной и обеспечивает предприятию наибольшую возмож­ную прибыль Z = 2250. При этом первый и второй ресурсы будут исполь­зованы полностью х₅ = 0, х₆ = 0 (узкие места производства), а третий ресурс будет иметь остаток х₇ = 7

0x₁ + х₂ + 3/5x₃ – 3/5x₄ + 1/5x₅ – 1/10x₆ + 0x₇ = 15

x₁ + 0х₂ – 1/5x₃ + 6/5x₄ – 1/15x₅ + 1/5x₆ + 0x₇ = 35

0x₁ + 0х₂ + 18/5x₃ + 32/5x₄ + 7/15x₅ – 1/10x₆+ x₇ = 7

общее решение системы условий

x₂ = 15 + 3/5x₃ – 3/5x₄ + 1/5x₅ – 1/10x₆

x₁ = 35 – 1/5x₃ + 6/5x₄ – 1/15x₅ + 1/5x₆

x₇ = 7 – 18/5x₃ + 32/5x₄ + 7/15x₅ – 1/10x₆

Z = 2250 + 6х₃ + 4x₄ + 15x₅ + 3x₆

Из этого выражения видно, что найденная производственная программа действительно является оптимальной, обеспечивает максимальную прибыль.

Проверим выполнение соотношения H=Q^-1 В, где Q^-1 базис в последней симплексной таблице, соответствующий набору базисных неизвестных.

Проверка: H=Q^-1*B

	1/5	–1/10	0
Q-1=	–1/15	1/5	0
	–7/15	–1/10	1
		1/5	–1/10	0		180		15
H=	Q-1*B=	–1/15	1/5	0	*	210	=	30
		–7/15	–1/10	1		112		7

1/5 *180–1/10*210+0*112 = 36–21 = 15

–1/15*180+1/5*210+0*112 = –12+42 = 30

–7/15*180–1/10*210+1*112 = –84–21+112 = 7

Вывод: при решении симплексной таблицы ошибок допущено не было.