
Математическая_Статистика_КР8
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
(теория, практика, контрольная работа №8)
Ростов-на-Дону
2010
1
УДК 517(07)
Математическая статистика (теория, практика, контрольная работа №8). — Рос- тов-на-Дону: Ростовский государственный строительный университет, 2010, – 71 с.
Пособие предназначено для студентов очной и заочной формы обучения. Содержит основные понятия математической статистики, описание статистических методов первичной обработки данных, методы проверки статистических гипотез, примеры с подробными решениями. Приведены контрольные задания.
Кафедра прикладной математики и вычислительной техники РГСУ Составители: д.т.н. Белявский Г.И. к.ф.-м.н. Мисюра В.В.
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ, 2010
2
Предметом математической статистики является изучение случайных величин (или случайных событий) по результатам наблюдений.
Совокупность всех подлежащих изучению объектов или возможных результатов всех мыслимых наблюдений, проводимых в неизменных условиях над одной из случайных величин, связанных с данным видом объектов, называется генеральной совокупностью.
Часть отобранных объектов из генеральной совокупности (результаты наблюдений над ограниченным числом объектов из этой совокупности) называется выборочной совокупностью или выборкой. Для того чтобы по выборке можно было достаточно уверенно судить о случайной величине, выборка должна быть представительной (репрезентативной). Репрезентативность выборки означает, что объекты выборки достаточно хорошо представляют генеральную совокупность. Репрезентативность выборки обеспечивается, согласно закону больших чисел, случайностью отбора. Последнее означает, что любой объект выборки отобран случайно, при этом все объекты имеют одинаковую вероятность попасть в выборку.
Различают выборки с возвращением (повторные) и без возвращения (бесповторные). В первом случае отобранный объект возвращается в генеральную совокупность перед извлечением следующего, во втором — не возвращается.
1.Способы первичной обработки выборки
Пусть некоторый признак генеральной совокупности описывается случайной величиной X. Рассмотрим выборку {x1 ,x2 ,...,xn }, состоящую из n наблюдений
(при этом п называется объемом выборки).
Полученный первичный статистический материал подлежит дальнейшей обработке, прежде всего упорядочению. Операция, заключающаяся в том, что результаты наблюдений над случайной величиной, т. е. наблюдаемые значения случайной величины, располагают в порядке неубывания, называется ранжированием опытных данных. Ранжированная совокупность опытных данных называется ва-
риационным рядом
Если в выборке число х1 повторяется m1 раз, число х2 – m2 раза,…, число хk – mk раз (т. е. выборка содержит k различных значений случайной величины), то числа xi называются вариантами, соответствующие им mi – частотами (абсо-
лютными частотами). При этом m1 + m2 + ... + mk = n .
При этом вместо абсолютных частот mi можно задавать распределение относительных частот (частость).
Отношение частоты данного варианта к общей сумме частот всех вариантов называется частостью или относительной частотой этого варианта и обозначается pi , где i — индекс варианта
3
p |
= |
mi |
или p |
= |
mi |
. |
|
|
|
||||||
i |
|
k |
i |
|
n |
(1.1) |
|
|
|
∑mi |
|
|
|||
|
|
|
|
|
|
|
|
i=1
Ранжированная совокупность вариантов и соответствующих им частот или частостей называется дискретным статистическим рядом или статистическим распределением выборки.
Записывается статистическое распределение в виде таблицы. Первая строка содержит варианты, вторая — их частоты или частости.
Пусть для дискретной случайной величины X по выборочным данным построен дискретный статистический ряд, в котором каждому варианту xi – ставится в соответствие его частость pi . Очевидно, что ∑pi равны 1. Тогда статистиче-
ское распределение выборки является оценкой неизвестного распределения дискретной случайной величины X. Естественно считать частость pi выборочным
аналогом (вычисленной по выборочным данным) вероятности рi, появления значения xi, случайной величины X, так как частость (статистическая вероятность) pi
обладает свойством устойчивости, или, иначе, при выполнении определенных условий (см. теоремуБернулли) стремится по вероятности к вероятности pi.
Пример 1.1. Дана выборка, состоящая из чисел: 3.2, 5.0, 7.5, 7,5, 6.7, 4.4, 4.4, 5.0, 5.0, 6.7, 6.7, 7.5, 3.2, 4.4, 6.7, 6.7, 5.0, 5.0, 4.4, 8.1. Построить дискретный статисти-
ческий ряд.
Решение.
Объем выборки п = 20. Перепишем варианты в порядке возрастания: 3.2, 3.2, 4.4, 4.4, 4.4, 4.4, 5.0, 5.0, 5.0, 5.0, 5.0, 6.7, 6.7, 6.7, 6.7, 6.7, 7.5, 7.5, 7.5, 8.1.
Составлен вариационный ряд, который показывает, что выборка состоит из шести вариантов.
Составим дискретный статистический ряд:
xi |
3,2 |
|
4,4 |
5 |
6,7 |
7,5 |
8,1 |
mi |
2 |
|
4 |
5 |
5 |
3 |
1 |
pi |
0,1 |
|
0,2 |
0,25 |
0,25 |
0,15 |
0,05 |
(частость |
pi = mi |
). ► |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
Если получена выборка значений непрерывной случайной величины, где отдельные значения случайной величины могут как угодно мало отличаться друг от друга и поэтому в совокупности наблюдаемых данных одинаковые значения величины могут встречаться редко, а частоты вариантов мало отличаются друг от друга, составляется сгруппированный (интервальный) статистический ряд.
Нецелесообразно также построение дискретного ряда для дискретной случайной величины, число возможных значении которой велико. В подобных случаях следует также построить интервальный ряд распределения.
4
Для построения такого ряда весь интервал варьирования наблюдаемых значений случайной величины разбивают на ряд частичных интервалов и подсчитывают частотупопадания значений величины в каждый частичный интервал.
Интервальный статистистический ряд — это упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частотами или частостями попаданий в каждый из них значений величины.
Для построения интервального ряда необходимо определить величину частичных интервалов, на которые разбивается весь интервал варьирования наблюдаемых значений случайной величины. Считая, что все частичные интервалы имеют одну и ту же длину, для каждого интервала следует установить его верхнюю и нижнюю границы, а затем в соответствии с полученной упорядоченной совокупностью частичных интервалов сгруппировать результаты наблюдений. Длину частичного интервала h следует выбрать так, чтобы построенный ряд не был громоздким и в то же время позволял выявить характерные черты изменения значений случайной величины, т. е. характерные черты изучаемого явления.
Длина интервала вычисляется по формуле
h = |
xнаиб − xнаим |
или h = b −a |
(k — количество интервалов, неко- |
(1.2) |
|
k |
|||||
|
k |
|
торый интервал (a,b) содержит все варианты),
в качестве абсолютных частот выступают количества вариантов, попавших в данный интервал. Если наблюдаемое значение находится на границе интервала, то его присоединяют к правомуинтервалу.
Для более точного определения величины частичного интервала можно воспользоваться формулой Стерджеса
h = (xнаиб − xнаим ) k , где k =1+1.4ln n . |
(1.3) |
k — число интервалов. Если окажется, что k — дробное число, то число интервалов следует брать либо ближайшее целое число, либо целую часть числа.
За начало первого интервала рекомендуется брать величину xнач=xнаим-0,5h.
Конец последнего интервала (хкон) должен удовлетворять условию
xкон −h ≤ xнаиб < xкон
Промежуточные интервалы получают, прибавляя к концу предыдущего интервала длину частичного интервала h. Очевидно, что получаем k+1 интервал.
Пример 1.2. Дана выборка: |
|
|
|
|
|
|
|
|
|
|
|
|||||
5,4 |
3,9 |
12,2 |
2,6 |
8,5 |
5,0 |
5,0 |
1,3 |
3,8 |
4,2 |
6,1 |
2,6 |
5,1 |
3,4 |
3,4 |
4,3 |
6,3 |
10,5 |
8,4 |
10,2 |
0,8 |
1,7 |
4,8 |
1,5 |
5,7 |
1,6 |
6,5 |
14,4 |
1,4 |
0,2 |
|
|
|
|
Построить интервальный статистический ряд.

5
Решение.
Объем выборки п = 30. Выполним ранжирование выборки:
0,2 |
0,8 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
2,6 |
2,6 |
3,4 |
3,4 |
3,8 |
3,9 |
|
|
|
|
4,2 |
4,3 |
4,8 |
5 |
5 |
5,1 |
5,4 |
5,7 |
6,1 |
6,3 |
6,5 |
8,4 |
8,5 |
10,2 |
10,5 |
12,2 |
14,4 |
|
Обратите внимание, что одинаковые значения случайной величины встре- |
|||||||||||||||
чаются редко, частоты вариантов мало отличаются друг от друга. |
|
|
|
|||||||||||||
|
Просматривая приведенные выше результаты наблюдений, находим, что |
|||||||||||||||
наибольшим значением случайной величины (xнаиб) является |
14,4, а |
наимен ь- |
||||||||||||||
шим |
(хнаим) – 0,2. |
Тогда xнаиб −xнаим =14,4 −0,2 =14,2. |
|
|
|
|
|
|
||||||||
Найдем число интервалов k и длинуинтервалов h по формуле Стерджеса.
k =1+1,4 ln(30) ≈ 5,7. Поскольку k должно быть целым числом, возьмем целую часть от числа 5,7, k=5.
Найдем h = 145,2 = 2,84 .
Отступаем на полшага h от наименьшего значения выборки – 0,2 − 2,284 = −1,22. Промежуточные интервалы получаем прибавляя к концу пре-
дыдущего интервала длину частичного интервала h (в рассматриваемом случае h=2,84).
Статистический ряд при этом имеет вид:
Номер интервала |
Границы |
Абсолютные |
Относительные |
|
|
интервала |
частоты |
частоты |
|
1 |
-1,22 — 1,62 |
6 |
6 30 |
|
2 |
1,62 |
— 4,46 |
9 |
9 30 |
3 |
4,46 — 7,3 |
9 |
9 30 |
|
4 |
7,3 — 10,14 |
2 |
2 30 |
|
5 |
10,14 |
— 12,98 |
3 |
3 30 |
6 |
12,98 |
— 15,82 |
1 |
1 30 |
Из таблицы видно, что в четвертый интервал попало 2 значения случайной величины. Однако определенно нельзя сказать, каковы эти значения, зато можно утверждать, что все эти значения принадлежат интервалу [7,3; 10,14). Такие частоты обычно называют интервальными, а их отношение к общему числу наблю- дений—интервальными частостями.
При вычислении интервальных частостей округление результатов следует проводить таким образом, чтобы общая сумма частостей была равна 1. ►
Одним из способов обработки вариационного ряда является построение эмпирической функции распределения.
6
В теории вероятностей для характеристики распределения случайной величины X служит интегральная функция распределения F(x) = P(X ≤ x). Введем выборочный аналог функции F(x).
Пусть имеется выборочная совокупность значений некоторой случайной величины X объема n и каждому варианту из этой совокупности поставлена в соответствие его частость. Пусть, далее, х – некоторое действительное число, а mx – число выборочных значений случайной величины X, меньших либо равных х.
Выборочной функцией распределения (или функцией распределения выборки) называется функция, задающая для каждого значения х относительную час-
тоту события Х ≤ х.
F(x) задается аналитически с.о.
|
0 |
при |
х < х1 |
|
|
|
|
|
|
i−1 |
xi−1 ≤ x < xi , i =1,2,3,...,k, |
(1.4) |
||
F |
(x)= ∑ pl при |
|||
|
l=1 |
|
|
|
|
1 |
при |
x ≥ x |
|
|
|
|
v |
|
где xi (i =1,2,...,k) границы частичных интервалов.
Свойство статистической устойчивости частоты, обоснованное теоремой Бернулли, оправдывает целесообразность использования функции F(x) при больших n в качестве приближенного значения неизвестной функции F(x).
Количество вариантов mx , значения которых меньше
ленной частотой, т.е.
mx = ∑mi
xi ≤x
x , называется накоп-
(1.5)
Тогда число mx 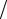 n является частостью наблюдаемых в выборке значений
n является частостью наблюдаемых в выборке значений
величины X, меньших либо равных х, т. е. частостью появления события Х ≤ х. При изменении х в общем случае будет изменяться и величина mx 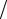 n. Это означа-
n. Это означа-
ет, что относительная частота mx  n является функцией аргумента х. А так как эта
n является функцией аргумента х. А так как эта
функция находится по выборочным данным, полученным в результате опытов, то ее называют выборочной или эмпирической. Отношение накопленной частоты к общемучислу наблюдений n обычно называют накопленной частостью:
ωx = mx = |
1 |
∑mi . |
n |
n x ≤x |
|
|
|
i |
Тогда эмпирическую функцию распределения можно определить с.о.
F(x)= |
0 |
|
при |
х < х1 |
|
|
m |
x |
n |
при x |
≤ x < x |
, i =1,2,3,...,k, |
|
|
|
|
i−1 |
i |
|
|
|
|
|
при |
x ≥ xk. |
|
|
|
1 |
|
|
|
(1.6)
(1.7)

7
Пример 1.3. Для данных примера 1.1 построить эмпирическую функцию распределения.
Решение.
Найдем накопленные частоты и частости. Наименьший вариант равен 3,2, число наблюдений меньших либо равных 3,2 равно 2, значит, mx = 2 и
ωx = mnx = 202 . Если x = 4,4, число наблюдений меньших либо равных 4,4 равно 6,
значит, m |
x |
= 6 |
и ω |
x |
= |
mx |
= |
6 |
. Далее рассуждаем аналогично. Результаты вычис- |
||||||||||||
|
20 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||
лений запишем в виде таблицы. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
xi |
|
|
|
3,2 |
|
|
4,4 |
|
|
|
|
5 |
6,7 |
|
7,5 |
8,1 |
|
|
||
|
mxi |
|
|
|
2 |
|
|
|
6 |
|
|
|
|
11 |
16 |
|
19 |
20 |
|
|
|
|
ωx |
|
|
|
0,1 |
|
|
0,3 |
|
|
|
|
0,55 |
0,8 |
|
0,95 |
1 |
|
|
||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно |
|
|
(1.7) |
|
|
получаем |
эмпирическую |
функцию |
распределения |
||||||||||||
|
0, |
|
|
|
|
x < 3,2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
0,1, |
|
3,2 ≤ x < 4,4 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4,4 ≤ x < 5 |
|
|
|
|
|
|
|
|
|
|
||||||
0,3, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
F |
(x) = 0,55, |
5 ≤ x < 6,7 ► |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
6,7 ≤ x < 7,5 |
|
|
|
|
|
|
|
|
|
|
||||||
|
0,8, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
0,95, |
7,5 ≤ x <8,1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
x ≥8,1 |
|
|
|
|
|
|
|
|
|
|
|||
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В рассматриваемом примере функция F(x) построена по дискретному статистическому ряду и для дискретной случайной величины. Рассмотрим на примере построения функции F(x) по интервальному статистическому ряду для непрерывной случайной величины .
Пример 1.4. Используя данные примера 1.2, найдем выборочную функцию распределения.
Решение.
Найдем накопленные частоты и частости. Начало первого интервала равно -1,22, число наблюдений меньших либо равных -1,22 равно 0, значит, mx = 0 и
ωx = 0 . Далее x =1,62 , число наблюдений меньших либо равных 1,62 равно 6, значит, mx = 6 и ωx = mnx = 306 и т.д. Результаты вычислений запишем в виде таблицы.
xi |
-1,22 |
1,62 |
4,46 |
7,3 |
10,14 |
12,98 |
15,82 |
mx |
0 |
6 |
15 |
24 |
26 |
29 |
30 |
ωx |
0 |
6 30 |
15 30 |
24 30 |
26 30 |
29 30 |
1 |
|
|
|
|
|
8 |
|
|
|
|
|
|
Далее построим функцию распределения. |
|
|
|
|
|
|
|||||
|
|
Очевидно, что всех x (- ∞; -1,22) функция распределения равна 0, так как |
|||||||||
известно, что |
нет наблюдений меньших либо равных |
-1,22. Пусть |
теперь |
||||||||
x [ -1,22;1,62) . В этом случае значение выборочной функции распределения |
не |
||||||||||
определено, так как не известно, сколько выборочных значений случайной вели- |
|||||||||||
чины, |
принадлежащих |
этому |
интервалу, |
меньше |
х. |
Если |
х=1,62, |
то |
|||
F(x)=ωx (x =1,62) = 6 / 30. Рассуждая аналогично, убеждаемся, что точками, в ко- |
|||||||||||
торых значения функции F(x) можно определить, являются правые концы интер- |
|||||||||||
валов и все точки интервала [15,82;∞). Определяем теперь значение функции |
|||||||||||
F(x) в указанных точках и запишем в виде таблицы. |
|
|
|
|
|
||||||
xi |
|
-1,22 |
1,62 |
4,46 |
7,3 |
10,14 |
|
12,98 |
|
15,82 |
|
F(x) |
0 |
6 30 |
15 30 |
24 30 |
26 30 |
|
29 30 |
|
1 |
|
|
|
|
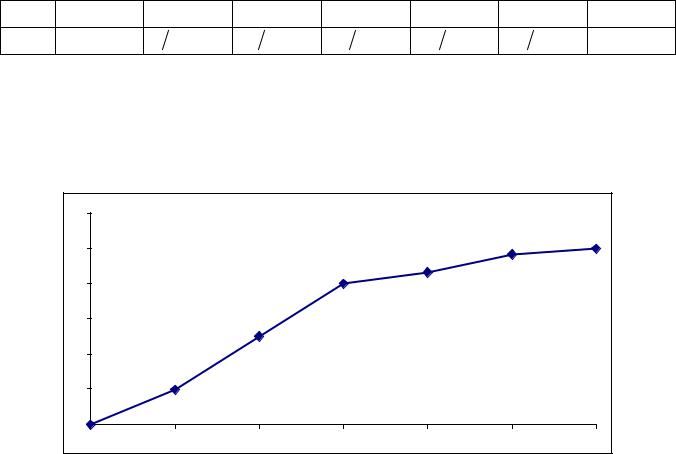
Так как эта таблица определяет функцию F(x) не полностью (не для всех х |
|||||||||
известны ее значения), то при графическом изображении данной функции целе- |
|||||||||||
сообразно ее доопределить, соединив точки графика, соответствующие концам |
|||||||||||
интервалов, отрезками прямой (рис.1.1). В результате график функции F(x) будет |
|||||||||||
представлять собой непрерывную линию. |
|
|
|
|
|
|
|||||
|
|
1,2 F(x)( mx |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
0,8 |
|
|
|
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
x |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
-1,22 |
1,62 |
4,46 |
7,3 |
10,14 |
|
12,98 |
15,82 |
|
|
|
|
|
|
|
Рисунок 1.1. |
|
|
|
|
|
|
Обратите внимание, что на концах частичных интервалов значение эмпирической функции распределения F(x) и значение накопленной частости ωx совпадают. ►
Для наглядного представления поведения случайной величины, исследуемой по выборке, используют графические изображения статистических рядов в виде полигона, гистограммы и кумулянты.
Полигон служит, как правило, для изображения дискретного статистического ряда и представляет собой ломаную, соединяющую точки плоскости с коорди-
натами (xi ,mi ) , i =1,2,...,n. Для интервального ряда полигон строится по точкам (ci ,mi ) , где ci —середина i-го интервала.
