Математическая_Статистика_КР8

37

ν

∑ni = n .

i=1

С помощью критерия Пирсона можно проверить гипотезу о различных законах распределения генеральной совокупности (равномерном, нормальном, показательном и др.)

Схема применения критерия χ2 для проверки гипотезы H0 сводится к следующему.

1. Формулируют основную гипотезу H0 , которая заключается в том, что

исследуемая случайная величина X подчиняется определенному закону распределения.

2.По результатам наблюдений находят оценки неизвестных параметров этой модели (допустим, что их число равно r).

3.Вместо неизвестных параметров подставляют в модель закона найденные

оценки.

4.В результате предполагаемая модель закона оказывается полностью оп-

ределенной и, используя ее, рассчитывают вероятности pi теор = P(X = xi ) , того,

что случайная величина X примет зафиксированные в наблюдениях значения xi , i =1,2,...,ν . Эти вероятности называют теоретическими.

5.Находят теоретические частоты ni′ = npiтеор .

6.В качестве критерия выбирается случайная величина

– число частичных интервалов выборки или вариант, r – число параметров предполагаемого распределения.

7. Критическая область выбирается правосторонней, и граница ее при заданном уровне значимости α χкр2 (α,k) находится по таблице критических точек

распределения χ2 (см. приложение 4).

Это значит, что если χ2 > χкр2 (α,k) , то гипотеза H0 отвергается, в противном случае принимается.

Замечание: Критерий согласия Пирсона можно использовать лишь в том

случае, когда ni′ ≥ 5. Если в какой-нибудь группе вариационного ряда это усло-

вие не выполняется, то имеет смысл объединить две соседние группы, так поступают до тех пор, пока для каждой новой группы не будет выполняться неравенство ni′ ≥ 5.

38

Приведем некоторые факты, необходимые для построения теоретического распределения по опытным данным.

Пусть по выборке объема n получен дискретный статистический ряд:

Проверки гипотезы о биномиальном законе распределения

◄ Для проверки гипотезы о биномиальном распределении генеральной совокупности в качестве оценки параметра p принимается p = mx , где m – число испыта-

Проверки гипотезы о законе распределения Пуассона

◄ Для проверки гипотезы о распределении генеральной совокупности по закону Пуассона в качестве оценки параметра λпринимается λ = x . Тогда теоретические

Пусть по выборке объема n получен интервальный статистический ряд:

Проверки гипотезы о нормальном законе распределения

◄ Для проверки гипотезы о нормальном распределении генеральной совокупности в качестве оценок параметров a и σ принимается соответственноa = х и

и xi+1 – левая и правая границы i-го интервала (i =1,2,...,ν ), x - выборочное среднее, s = 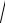s2 – выборочное среднее квадратическое отклонение. Поскольку нор-

39

мальное распределение характеризуется двумя параметрами, число степеней свободы k =ν −3. ►

Проверки гипотезы о показательном законе распределения

◄ Для проверки гипотезы о показательном распределении генеральной совокуп-

Проверки гипотезы о равномерном законе распределения

◄ Для проверки гипотезы о равномерном распределении генеральной совокупности концы интервала, в котором наблюдались возможные значения Х, оценива-

Число степеней свободы k =ν − 2 , так как равномерное распределение оценивается двумя параметрами. ►

Пример 6.5. Для выборки, интервальный статистический ряд которой имеет вид

Проверить при уровне значимости α = 0,05 гипотезу о: а) показательном; б) равномерном; в) нормальном

законе распределения генеральной совокупности с помощью критерия Пирсона.

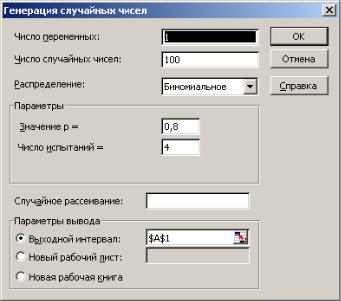
в) Теоретические частоты для нормального распределения:

купности принимается. ►

Приведем примеры проверки гипотезы о законе распределения случайной величины с помощью критерия Пирсона, выполненной средствами Microsoft Excel.

Пример 6.6. По успеваемости 100 студентов-заочников, которые сдавали 4 экзамена получена выборка. Необходимо проверить гипотезу о биномиальном законе распределения случайной величины.

Решим поставленную задачу с помощью Microsoft Excel.

1. В новой рабочей книге сгенерируем выборку с помощью Пакета анализа (Сервис/Анализ данных/Генерация случайных чисел). Понятно, что необходимо генерировать значения случайной величины, имеющей биномиальное распределение. Зададим вероятность успеха в одном испытании равной 0,8 (см. рис.6.1).

Рисунок 6.1.

Далее считаем, что полученная последовательность – выборка объемом n=100, характеризующая успеваемости 100 студентов-заочников, каждый из которых сдавал 4 экзамена. X — случайная величина равная числу сданных экзаменов одним студентом.

42

2. Выдвигаем основную гипотезу H0 : исследуемая случайная величина X имеет биномиальный закон распределения.

3. Далее выполняем шаги согласно схеме предложенной выше. Получаем лист Excel, представленный на рис.6.2. На рис.6.3 представлен лист Excel с формулами. Обратите внимание, что диапазон F20:F24 содержит формулу массива. Описательную статистику выполняем с помощью Пакета анализа (Сервис/Анализ данных/Описательная статистика).

При вычислении критерия число групп уменьшилось (почему?), число степеней свободы критерия вычислили с.о.: число групп минус один параметр минус единица, получили что число степеней свободы равно1. Задали уровень значимости равный 0,05.

Поскольку χ2 < χкр2 (α,k) , основную гипотезу H0 о виде распределения принимаем.

Пример 6.7. По данным выборочного обследования получена выборка среднедушевого дохода населения в тыс. рублей. Необходимо проверить гипотезу о нормальном законе распределения случайной величины.

Решим поставленную задачу с помощью Microsoft Excel.

1.В новой рабочей книге сгенерируем выборку с помощью Пакета анализа (см. рис.6.4). Будем считать, что СВ X — среднедушевой доход населения подчиняется нормальному закону распределения.

Далее считаем, что полученная выборка объемом n=100 характеризует среднедушевой доход населения.

2.Выдвигаем основную гипотезу H0 : исследуемая случайная величина X имеет

нормальный закон распределения.

44

Рисунок 6.4.

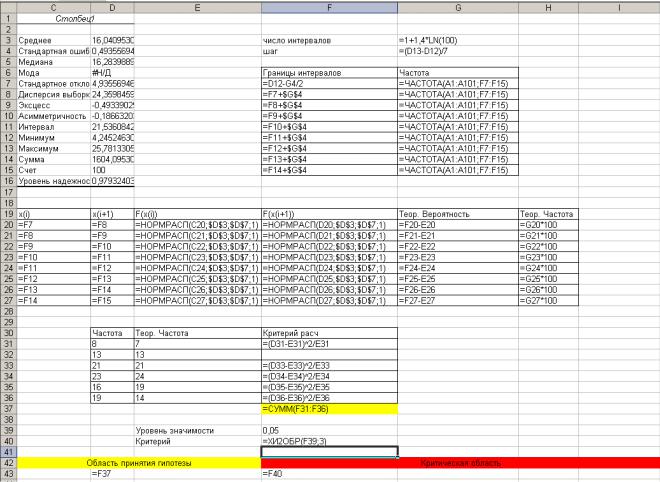
3. Далее выполняем шаги согласно схеме предложенной выше. Получаем лист Excel, представленный на рис.6.5 и на рис.6.6 представлен лист Excel с формулами.

Оценки параметров нормального распределения находятся в таблице Описательная статистика (Сервис/Анализ данных/Описательная статистика).

Заметим, что при получении теоретической вероятности для интервального статистического ряда вычисляется вероятность попадания в интервал по формуле

P( a < X < b ) = F( b ) − F( a ).

Обратите внимание, что диапазон G7:G15 содержит формулу массива.

При вычислении критерия диапазоны число групп уменьшилось (почему?), число степеней свободы критерия вычислили с.о.: число групп-два параметра-1, получили что число степеней свободы равно 3. Задали уровень равный 0,05.

Поскольку χ2 < χкр2 (α,k ), основную гипотезу H0 о виде распределения принима-

ем.

46

Рисунок 6.6.