Математическая_Статистика_КР8

Рисунок 1.2.

На рисунке 1.3 изображена кумулянта дискретного статистического ряда.

Рисунок 1.3.

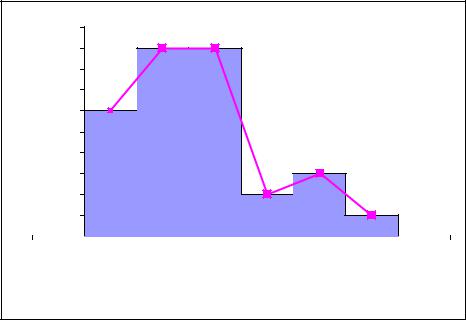
Построим гистограмму (рисунок 1.4) и полигон для интервального статистического ряда, рассмотренного в примере 1.2.

Кумулятивная кривая для интервального статистического ряда, рассмотренного в примерах 1.2 и 1.4, представлена на рисунке 1.1. Как отмечалось выше на концах частичных интервалов значение эмпирической функции распределения интервального статистического ряда и значение накопленной частости совпадают.

Статистические методы сравнительно просто реализуются в электронной таблице MS Excel. В Лабораторных работах 1 и 2, приведенных в конце методического пособия, рассматриваются практические методы построения дискретного и интервального статистического ряда.

Построив статистический ряд и изобразив его графически, можно получить первоначальное представление о закономерностях, имеющих место в ряду наблюдении. Однако на практике зачастую этого недостаточно. Такая ситуация возникает, когда следует уточнить те или иные сведения о ряде распределения или когда имеется необходимость сравнивать два ряда и более. При этом следует сравнивать однотипные статистические ряды, т.е. такие ряды, которые получены при обработке сравниваемых статистических данных.

Например, можно сравнивать распределения длины втулок, изготовленных на двух однотипных станках-автоматах, или распределения количества отказов определенных электронных устройств, изготовленных на разных заводах. Обычно графики таких распределений имеют почти одинаковый вид. Особенно это относится к кумулятивной кривой.

Сравниваемые распределения могут существенно отличаться друг от друга. Они могут иметь различные средние значения случайной величины, вокруг которых группируются в основном остальные значения, или различаться рассеиванием данных наблюдений вокруг указанных значений и т.д. поэтому для дальнейшего изучения изменения значений случайной величины используют числовые характеристики статистических рядов.

12

Медианой Me вариационного ряда называется значение признака, приходящееся на середину ряда.

Для вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов – полусумме двух серединных вариантов.

Модой Mо вариационного ряда называется вариант, имеющий наибольшую частоту.

Средние величины, рассмотренные выше, не отражают изменчивости (вариации) значений признака.

Простейшим показателем вариации является вариационный размах R, равный разности между наибольшим и наименьшим вариантами ряда:

Наибольший интерес представляют меры вариации (рассеивания) наблюдений вокруг средних величин, в частности, вокруг средней арифметической.

Выборочной дисперсией значений случайной величины X называется среднее арифметическое квадратов отклонений наблюдаемых значений этой величи-

ны от их среднего арифметического (обозначение DX ):

Если данные наблюдений представлены в виде дискретного статистического ряда (2.1.а), то выборочная дисперсия определяется формулой

Вычисленная по формулам (2.5) дисперсия называется взвешенной выборочной дисперсией. В случае интервального статистического ряда его заменяют дискретным (за xi принимают середину i-го интервала, а за mi – соответствующую интервальную частоту) и затем используют формулы (2.4), (2.5).

Можно показать, что D(X ) может быть подсчитана также по формуле

Дисперсия характеризует отклонение от средней в квадратных единицах измерения признака, поэтому используют такой показатель ,как среднее квадратическое отклонение, который измеряется в тех же единицах, что и изучаемый признак.

13

Выборочным средним квадратическим отклонением называется арифметический квадратный корень из выборочной дисперсии (обозначениеσx ).

Выборочное среднее квадратическое отклонение определяется формулой:

Вычисляется также безразмерная характеристика — выборочный коэффициент вариации, который равен процентному отношению выборочного среднего квадратического отклонения к средней арифметческой:

Если коэффициент вариации высок (более 35%), то выборочная совокупность считается неоднородной. Следовательно, использование среднего для ее характеристики является неверным. В этом случае используют моду или медиану.

Пример 2.1. В результате тестирования группа студентов набрала баллы: 5, 2, 3, 0, 1, 3, 4, 2, 1, 3, 5, 4, 1, 0, 5, 3, 3. Найти характеристики полученной выборки.

Решение.

Объем выборки равен 16.

Составим вариационный ряд: 0, 0, 1, 1, 1, 2, 2, 3, 3, 3, 3, 4, 4, 5, 5, 5.

Получим дискретный статистический ряд.

Используя формулы (2.1) – (2.9) и определения данные выше находим:

x = 0 2 +1 3 +2 2 +3 4 +4 2 +5 3 = 2,625; 16

D(X ) = 02 2 +12 3 + 22 2 +32 4 + 42 2 +52 3 − 2,6252 = 2,734; 16

σx = 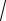2,734 =1,654 ;

14

s2 = 151 ( (0 − 2,625)2 2 + (1− 2,625)2 3 + (2 − 2,625)2 2 + (3 − 2,625)2 4 + + (4 − 2,625)2 2 + (5 − 2,625)2 3 )= 2,917;

s = 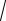2,917 =1,708;

R = 5 −0 = 5;

Mо = 3;

Me = 3 +2 3 = 3;

ν = 12,,654625 100% = 63% .►

Пример 2.2. Для выборки из примера 1.2 найдем выборочное среднее и исправленную выборочную дисперсию. Будем считать вариантами середины частичных интервалов.

s2 = (0,2 − 4,93)2 6 + (3,04 − 4,93)2 9 + (5,88 − 4,93)2 9 + (8,72 − 4,93)2 2 + (11,56 − 4,93)2 3 + (14,4 − 4,93)2 = 6,03;

29

s = 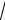6,03 = 2,45.

Проверьте самостоятельно, что вычисленные взвешенные выборочное среднее и дисперсия по интервальному ряду будет отличаться от значений, вычисленных по всей выборке с использованием формул (2.1), (2.5). ►

3. Точечная оценка параметров

Пусть изучается случайная величина X с законом распределения, зависящим от одного или нескольких параметров. Например, это параметр λ в распределении Пуассона, параметры a и σ для нормального закона распределения.

Выборку можно определить как последовательность X1, X 2 ,..., X n незави-

симых одинаково распределенных случайных величин, распределение каждой из которых совпадает с распределением генеральной случайной величины.

Конкретная выборка x1, x2 ,..., xn – это значения (реализация) независимых случайных величин X1, X 2 ,..., X n .

Требуется по выборке X1, X 2 ,..., X n , полученной в результате n наблюдений, оценить неизвестный параметр θ .

15

Выборочная характеристика θn , используемая в качестве приближенного

значения неизвестной генеральной характеристики θ , называется ее точечной статистической оценкой (далее просто – оценкой).

Очевидно, что оценка θn есть значение некоторой функции результатов наблюдений над случайной величиной, т.е.

Функцию результатов наблюдений называют статистикой.

Заметим, что выборочное среднее служит для оценки математического ожидания исследуемой случайной величины, выборочная дисперсия является оценкой дисперсии случайной величины.

Оценка θn является случайной величиной, так как является функцией независимых случайных величин X1, X 2 ,..., X n ; если произвести другую выборку, то функция примет, вообще говоря, другое значение.

Получив статистические оценки параметров распределения (выборочное среднее, выборочную дисперсию и т.д.), нужно убедиться, что они в достаточной степени служат приближением соответствующих характеристик генеральной совокупности. Определим требования, которые должны при этом выполняться.

Пусть θn - статистическая оценка неизвестного параметра θ теоретическо-

го распределения. Извлечем из генеральной совокупности несколько выборок одного и того же объема n и вычислим для каждой из них оценку параметра θ :

θn1,θn2 ,...,θnk Тогда оценку θn можно рассматривать как случайную величину, принимающую возможные значения θn1,θn2 ,...,θnk Если математическое ожидание θn не равно оцениваемому параметру, мы будем получать при вычислении оценок систематические ошибки одного знака (с избытком, если М(θn ) >θ , и с недостатком, если М(θn ) < θ ). Следовательно, необходимым условием отсутствия систематических ошибок является требование М(θn ) = θ .

Статистическая оценка θn называется несмещенной, если ее математическое ожидание равно оцениваемому параметру θ при любом объеме выборки:

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Однако несмещенность не является достаточным условием хорошего приближения к истинному значению оцениваемого параметра. Если при этом воз-

можные значения θn могут значительно отклоняться от среднего значения, то есть дисперсия θn велика, то значение, найденное по данным одной выборки, мо-

16

жет значительно отличаться от оцениваемого параметра. Следовательно, требуется наложить ограничения на дисперсию.

Статистическая оценка называется эффективной, если она при заданном объеме выборки n имеет наименьшую возможную дисперсию.

К статистическим оценкам предъявляется также требование состоятельно-

сти.

Состоятельной называется статистическая оценка, которая при n→∞ стремится по вероятности к оцениваемому параметру, т.е.

для любого ε > 0 выполнено limP(θn −θ <ε) =1.

n→∞

Это означает, что с увеличением объема выборки мы все ближе приближаемся к истинномузначению параметра θ , т.е. практически достоверно θn ≈θ .

Отметим важное утверждение, если оценка несмещенная θn , то она будет состоятельной, если при n→∞ ее дисперсия стремится к 0.

Убедимся, что х представляет собой несмещенную оценку математического ожидания М(Х).

Будем рассматривать х как случайную величину, а х1, х2,…, хn, то есть значения исследуемой случайной величины, составляющие выборку, – как незави-

симые, одинаково распределенные случайные величины X1, X 2 ,..., X n , имеющие математическое ожидание а. Из свойств математического ожидания следует, что

Но, поскольку каждая из величин X1, X 2 ,..., X n имеет такое же распределе-

ние, что и генеральная совокупность, а = М(Х), то есть М( Х ) = М(Х), что и требовалось доказать.

Выборочное среднее является не только несмещенной, но и состоятельной оценкой математического ожидания. Если предположить, что X1, X 2 ,..., X n имеют

ограниченные дисперсии, то из теоремы Чебышева следует, что их среднее арифметическое, то есть Х , при увеличении n стремится по вероятности к математическому ожиданию а каждой их величин, то есть к М(Х). Следовательно, выборочное среднее есть состоятельная оценка математического ожидания.

В отличие от выборочного среднего, выборочная дисперсия D(X )(см. (2.5), (2.6))является смещенной оценкой дисперсии генеральной совокупности. Можно

доказать, что М(D(X )) = n n−1 D(X ), где D(X )– истинное значение дисперсии генеральной совокупности.

17

Поэтому выборочную дисперсию исправляют, умножив ее на n n−1, получая исправленную выборочную дисперсию s2 (см. (2.9)).

Исправленная выборочная дисперсия s2 будет являться несмещенной. Отметим, что при больших значениях n разница между D(X ) и s2 очень

мала и они практически равны, поэтому оценку s2 используют для оценки дисперсии при малых выборках, обычно при n ≤ 30.

Далее рассмотрим точечную оценку генеральной доли p признака A ( p = MN

, где N — объем генеральной совокупности, M — количество элементов генеральной совокупности, обладающих некоторым признаком A).

Пусть m — число элементов выборки объема n, обладающих признаком A и ω = mn — выборочная доля признака A. Доказано, что ω является несмещенной и состоятельной оценкой генеральной доли p признака A.

4. Распределение функций нормальных случайных величин

Рассмотрим распределение некоторых случайных величин, представляющих функции нормальных величин, используемые в математической статистике.

1) Распределение χ2 (k). Пусть независимые случайные величины U1, U2,

…,Uk являются стандартными нормально распределенными величинами, т.е. Ui=N(0.1), i=1, 2, …, k. Распределение случайной величины

(6.33)

называется распределением хи-квадрат с k степенями свободы, а сама величина (4.1) – величиной хи-квадрат с k степенями свободы.

Подобно тому, как математическое ожидание a и среднее квадратическое отклонение σ являются параметрами нормального закона, так и число k является

параметром χ2 (k) - распределения.

Формула функции плотности χ2 (k) - распределения имеет сложный вид,

поэтому здесь не приводится. Графики этой функции – кривые Пирсона – при k=1, 2, 6 изображены на рисунке 4.1.

18

Рисунок 4.1.

В Приложении 4. содержатся определенные значения величины χ2 (k). Применение χ2 (k)-распределения рассматривается ниже.

2)Распределение Стьюдента. Пусть U – стандартная нормально распреде-

ленная случайная величина, т.е. U=N(0,1), а χ2 (k) случайная величина, имеющая

хи-квадрат-распределение с k степенями свободы, причем U и χ2 (k)– независимые величины. Распределение случайной величины

называется t-распределением с k степенями свободы или распределением Стьюдента, а сама величина (4.2) t-величиной с k степенями свободы.

Графики распределения величины t(k) – кривые Стьюдента – при k=1, 10 изображены на рисунке 4.2.

Рисунок 4.2.

В таблице Приложения 2 содержатся такие значения tγ величины t(k), при которых вероятность P(t(k) < tγ )= γ .