2. Вычисление двойного интеграла

Существуют два основных вида области интегрирования:

1.Область интегрирования Д ограничена слева и справа прямыми х = а,

х = в (а  в), а снизу и сверху - непрерывными кривыми у = ₁(х) и у =₂(х)

(₁(х)  ₂(х)), каждая из которых пересекается прямой, параллельной оси Оу, только в одной точке (рис. 1).

У

у = (х)

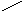
у = ₁(х)

Д

Х

а

в

Рис. 1

У

х = ₁(у)

х = ₂(у)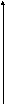

d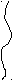

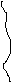
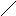
Д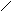

c

Х

Рис. 2

Вычисление двойного интеграла сводится к двукратному интегрированию

.

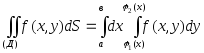Интеграл 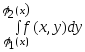называется внутренним. В немх считается постоянной. Этот интеграл вычисляется в первую очередь. А потом вычисляется внешний интеграл по переменной х.

Для того, чтобы поставить пределы внутреннего интеграла, надо посмотреть на изменение у вдоль вектора от точки входа вектора в областьД (нижний предел) до точки выхода вектора из области Д (верхний предел). Пределы внешнего интеграла всегда постоянны и показывают пределы изменения переменной х.

2. Пусть область интегрирования Д ограничена снизу и сверху прямыми

у = с, у = d (с  d) , а слева и справа - непрерывными кривыми х = ₁(у), х = ₂(у) (₁ (у)  ₁ (у)), каждая из которых пересекается горизонтальной прямой только в одной точке (рис. 2).

Тогда двойной интеграл по такой области вычисляется по формуле

,

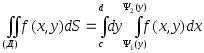причем сначала вычисляется внутренний интеграл, 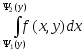, в которому считается постоянной.

Задача № 13

Вычислить повторные интегралы

1.;2. .

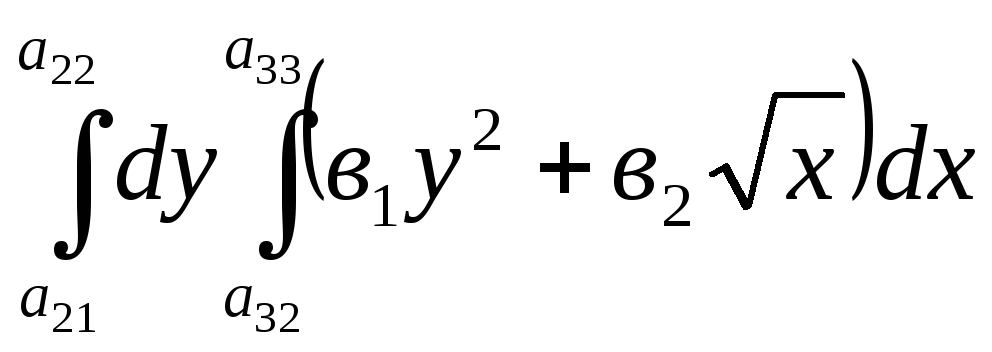1.

.

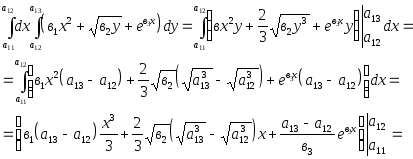
2.

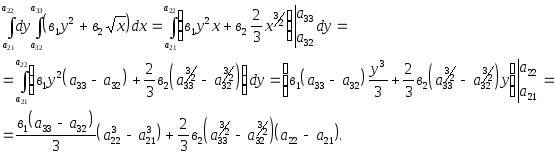
Задача № 14

Вычислить следующие двойные интегралы по области Д, ограниченные линиями

1.; 2. .

1. ;.

D

Х

У

.

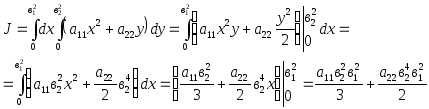
2. ;;

Y

Д

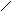
X

=

=

=

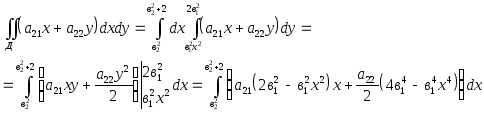
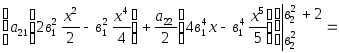
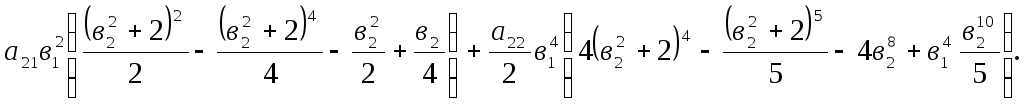
Контрольная работа №4 дифференциальные уравнения

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1-ГО ПОРЯДКА

Дифференциальными уравнениями ( д. у.) 1-го порядка называются уравнение вида F(x, у, у) = 0 (1)

или у = f(x, у), что можно записать и так (1)

dу = f(x,у)dx. (1)

Обозначим через Д область существования решения (1) - (1).

Общим решением д.у. (1) - (1) называется функция у =, (2)

где С - произвольная константа, удовлетворяющая условиям:

а) она является решением д.у. при любом С;

б) при любых начальных условиях . (*)

, найдется такое значение С = С₀ , что функция

удовлетворяет условиям (*).

Нахождение такого С = С₀ по условиям (*) называется решением задачи Коши. Найденная таким образом функция называется иначе частным решением д.у.

Если решение д.у. найдено в виде Ф(х, у, С) =0, оно называется общим интегралом этого уравнения.

1. Д.у. с разделяющимися переменными.

Общий вид : m₁(x) * m₂(y) dx + n₁(x) * n₂(y)dx = 0, (m₂(y)  0 и n­₁(x)  0 ). (3)

Разделим переменные: . Тогда является общим интегралом уравнения (3)

2. Однородные д.у.

Общий вид: у = f(x,y), (4)

где f(x,y) - однородная функция “нулевого измерения”, что означает выполнение условия f(tx,ty) = f(x,y) для любого t. (4) может быть приведено к виду (4):

. (4)

Подставной у = u * x приводится к уравнению с разделяющимися переменными : y = ux + u.

; -

общий интеграл уравнения (4).

3. Линейное д.у. 1-го порядка.

Общий вид:

у + Р(х) * у = Q (х) . (5)

Подстановка y = u * V, где u = u(x), V = V(x); y = uV + uV.

uV + uV + P(x) * uV = Q(x). (5)

Выберем V так, чтобы V + P(x) * V = 0. Это - д.у. с разделяющимися переменными.

, тогда (5) будет иметь вид:

uV = Q (x), а это также д.у. с разделяющимися переменными (V уже найдено!): 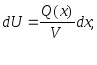интегрируя, получим: .

Окончательно, . Общий вид (5).

4. Уравнение Бернулли.

Общий вид: y + P(x) * y = Q(x) * yⁿ (6)

(n  0 и n  1). Метод решения - такой же, как линейного уравнения (5).