
- •Интегральное исчисление
- •1. Интегральное исчисление
- •Основные свойства неопределенного интеграла
- •Найти неопределенный интеграл .
- •Метод подстановки
- •Найти неопределенный интеграл .
- •Задача № 8
- •Теорема существования определенного интеграла
- •Вычисление объема тела вращения
- •Задача № 12
- •Двойной интеграл
- •Двойной интеграл в прямоугольных координатах
- •Вычисление двойного интеграла
- •Задача № 13
- •Задача № 14
- •Контрольная работа №4 дифференциальные уравнения
- •Задача № 1
- •Основные определения
- •Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами однородные уравнения
- •Задача № 2
- •Неоднородные уравнения случай специальной правой части
- •Задача № 3
- •Пояснение
- •Контрольная работа
- •Высшей математике (часть 2) Студента(ки) группы _________________________________________________
Найти неопределенный интеграл .
![]() =
=![]()
![]()
Метод подстановки
Метод заключается в том, что вместо переменной x вводят новую переменную, например t. Так, если положить х = (t), то
![]() Получаемый
интеграл должен быть значительно проще
данного. В противном случае следует
искать другую форму введения новой
переменной. Часто переменную
t
вводят так:
t
= (x),
а dt
= (x)dx.
Это удобно, если данное подынтегральное
выражение содержит дифференциал (x)dx.
Получаемый
интеграл должен быть значительно проще
данного. В противном случае следует
искать другую форму введения новой
переменной. Часто переменную
t
вводят так:
t
= (x),
а dt
= (x)dx.
Это удобно, если данное подынтегральное
выражение содержит дифференциал (x)dx.
ПРИМЕР:
![]()
Видно, что Cosx dx является дифференциалом для функции Sinx = t, Cosx dx = dt.
Получим
![]() (далее нужно вернуться к функцииSinx)
(далее нужно вернуться к функцииSinx)
![]()
ЗАДАЧА № 2
Найти неопределенный интеграл .
![]() =
=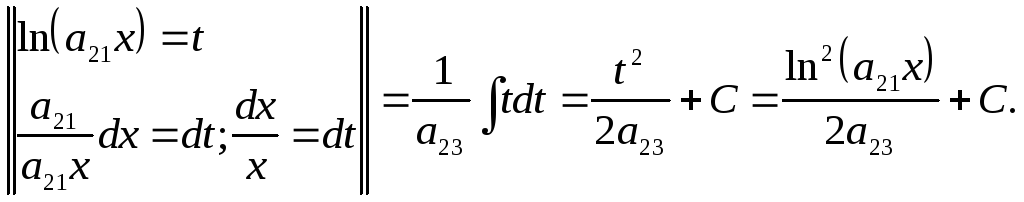
ЗАДАЧА № 3
Найти
неопределенный интеграл
![]() .
.
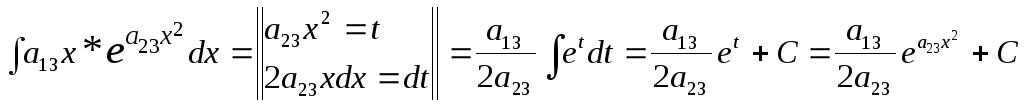 .
.
ЗАДАЧА № 4
Найти неопределенный
интеграл
![]() .
.
![]() =
=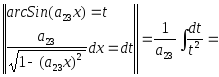
![]()
ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ КВАДРАТНЫЙ ТРЕХЧЛЕН
В квадратном трехчлене ах2 + вх + С следует выделить полный квадрат:
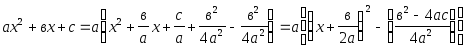 .
.
ПРИМЕР:
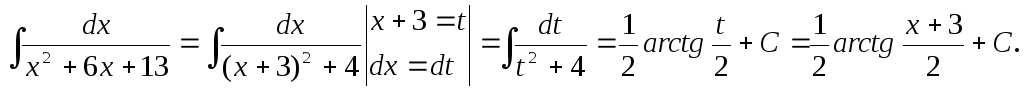
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
Идея
метода состоит в том, что подынтегральное
выражение f(x)dx
нужно представить в виде произведения
U*dV
, где U(x)
и V(x)
- дифференцируемые
функции и воспользоваться формулой
![]() .
.
При
этом вновь полученный интеграл
![]() должен
быть проще данного.
должен
быть проще данного.
ЗАДАЧА № 5
Найти
неопределенный интеграл
![]() .
.
![]() =
=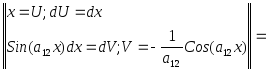
![]()
ЗАДАЧА № 6
Найти
неопределенный интеграл
![]() .
.
![]() =
=
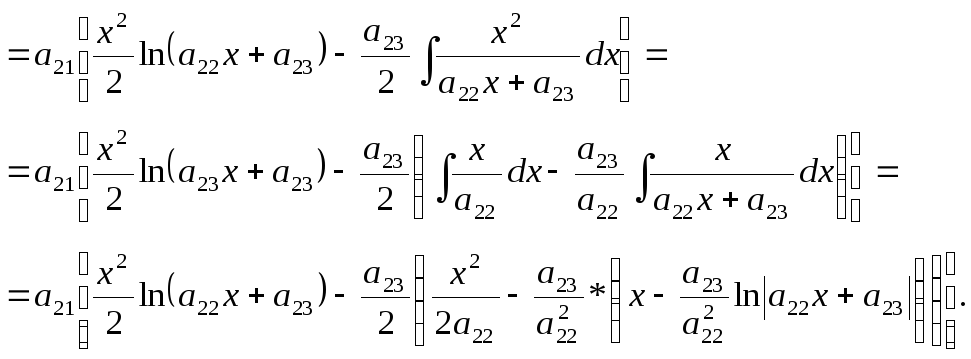
ЗАДАЧА № 7
Найти неопределенный
интеграл
![]() .
.
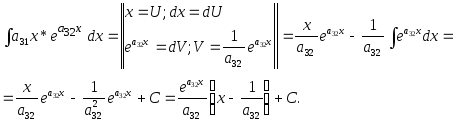
ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ
Выше было показано, что из неправильной рациональной дроби можно выделить целую часть и представить эту дробь как сумму целой ее части и правильной дроби. Поэтому будем рассматривать только интегрирование правильных дробей.
Всякую правильную рациональную дробь нужно представить в виде суммы простейших, которые имеют вид:
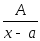 ,
2.
,
2.
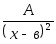 ,
3.
,
3.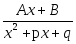 ,
,
где А, В, а, в, р, q - действительные числа.
Теперь нужно научиться всякую правильную рациональную дробь представить как сумму простейших. Для этого вначале разложим знаменатель этой дроби на произведение множителей типа (х - а) и (х2 + рх + q), причем квадратный трехчлен х2 + рх + q имеет дискриминант Д 0. Если Д 0, то такой квадратный трехчлен можно разложить на линейные множители:
x2 + px + q = (x - x1)(x - x2), где х1 и х2 - корни данного трехчлена.
Будем руководствоваться следующими приемами:
Каждому линейному множителю вида (х - а) соответствует дробь
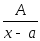 ,
гдеА
-
,
гдеА
-
неизвестный пока коэффициент;
2. Каждому множителю (х - в )к соответствует сумма из К простых дробей
![]() ;
;
3.
Каждому множителю
х2
+ рх + q
( Д
0 ) соответствует
дробь вида
![]() .
.
Задача № 8
Найти
неопределенный интеграл
![]() .
.
![]() ;
;
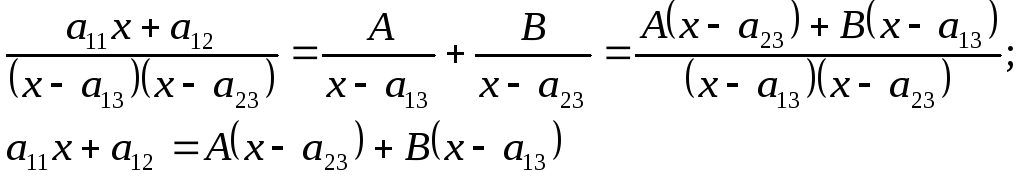
При х = а23 получим: а11а23 + а12 = В(а23 - а13).
При х = а13 получим: а11а13 + а12 = А(а13 - а23).
Отсюда
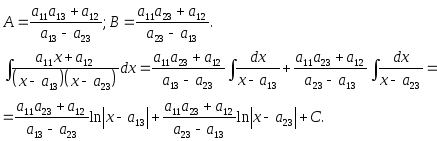
ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Рассмотрим интегралы вида:
![]() ,
где R
- рациональная
функция.
,
где R
- рациональная
функция.
Такие интегралы вычисляются при помощи универсальной подстановки
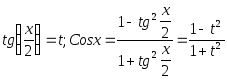 .
Тогда
.
Тогда
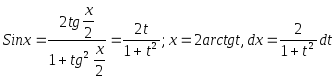 .
.
После
подстановки интеграл примет вид
![]() гдеR1(t)
- рациональная функция.
гдеR1(t)
- рациональная функция.
ПРИМЕР:
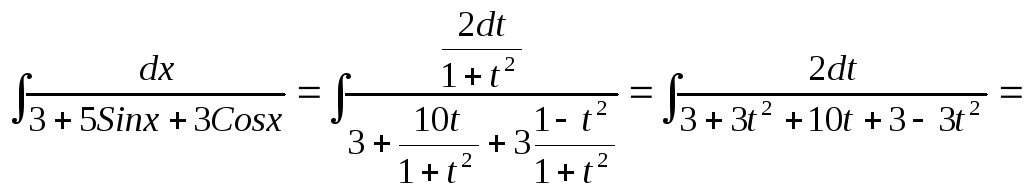
![]() .
.
Если
интегралы имеют вид:
![]() ,
то выполняют подстановку tgx
= z.
Используя тригонометрические
преобразования, получим
,
то выполняют подстановку tgx
= z.
Используя тригонометрические
преобразования, получим
![]() .
.
ПРИМЕР:
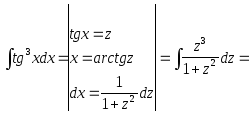 (выделим
целую часть неправильной дроби)
(выделим
целую часть неправильной дроби)
![]() .
.
Интегралы
вида:
![]() .
.
Рассмотрим 2 случая.
Случай 1
Хотя бы один из показателей - целое положительное нечетное число. Если положительное нечетное число n, то применяется подстановка Sinx = t, если
m - нечетное положительное число, то используется подстановка Cosx = t.
Случай 2
Оба показателя степени m и n - положительные четные числа. В этом случае необходимо преобразовать подынтегральную функцию с помощью формул понижения степени.
ПРИМЕР:
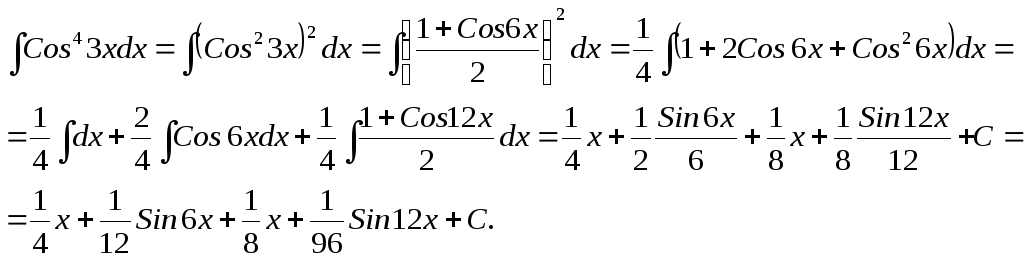
Интегралы
вида :
![]() .
.
Если степень подынтегральной функции n - целое положительное число, то такие интегралы вычисляются при помощи замены tgx = t или ctgx = t.
Интегралы
вида:
![]() .
.
В результате использования тригонометрических формул
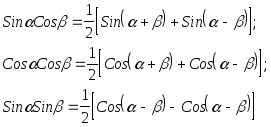
подынтегральные функции удается представить в виде суммы функций.
ПРИМЕР:
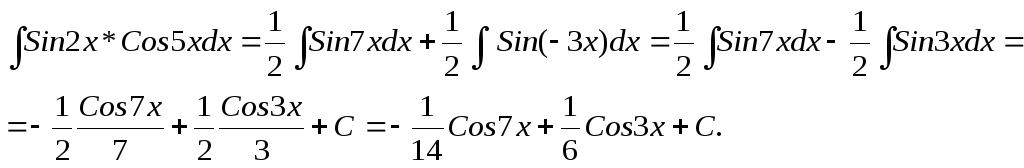
ЗАДАЧА № 9
Найти
неопределенный интеграл
![]() .
.
![]() =
=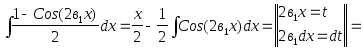
=![]()
ЗАДАЧА № 10
Найти
неопределенный интеграл
![]() .
.
![]() =
=![]()
=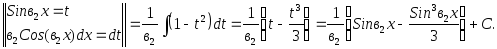
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пусть функция f(x) определена на отрезке [ a, в ]. Разделим отрезок
[ a, в ] на n произвольных частей точками а = х0 х1 х2 ... хn-1 хn = в.
Выберем
на каждом элементарном отрезке
[ Xk-1,
Xk
] произвольную
точку Сk,
обозначим длину элементарного отрезка
через
![]() хk
= xk
- xk-1.
хk
= xk
- xk-1.
Интегральной суммой для функции f(x) на отрезке [ a, в ] называется сумма вида
![]() .
.
Определение:
Определенным
интегралом от функции f(x)
на отрезке [
a,
в ] называется
предел интегральной суммы при условии,
что длина наибольшего из элементарных
отрезков стремится к нулю
![]() .
.
