9.4.2.Краевые условия

Дифференциальное уравнение (9.12) описывает в самом общем виде все без исключения задачи теплопроводности. Для решения конкретной задачи необходимо к дифференциальному уравнению присоединить математическое описание частных ее особенностей. Эти дополнительные данные, которые характеризуют конкретное единичное явление, называются краевыми условиями, или условиями однозначности.

Существуют различные условия однозначности: геометрические — характеризующие форму и размеры тела, в котором протекает про­цесс теплопроводности; физические — характеризующие физические свойства тела; временные — характеризующие распределение температуры тела в начальный момент времени; граничные — характеризующие взаимодействие тела с окружающей средой. Граничные условия в свою очередь бывают трех родов:

1) первого рода, задается распределение температуры на поверхности тела в функции времени;

2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;

3) третьего рода, задаются температура окружающей среды t_жи закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана:

,

(9.13)

где t_c— температура поверхности тела;α— коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м²·К). Коэф­фициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус. Этот коэффициент учитывает все особенности явлении теплообмена, происходящие между поверхностью тела и окружающей средой. Плотность теплового потока, передаваемого от поверхности тела в окружающую среду,

.

(9.14)

Согласно закону сохранения энергии, эта теплота равна теплоте, подводимой к поверхности изнутри тела путем теплопроводности:

.

Переписав последнее уравнение в виде:

,

(9.15)

получаем математическую формулировку граничных условий третьего рода. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье — соответствующие тепловые потоки.

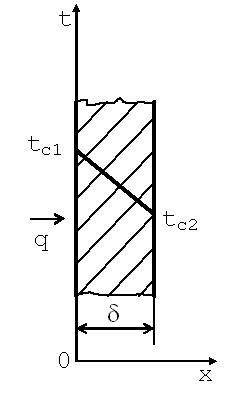
9.4.3.Теплопроводность через плоскую стенку при граничных условиях первого рода

Рис. 9.2. Однородная плоская стенка

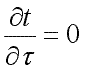Рассмотрим однородную плоскую стенку толщинойδ(рис. 9.2). На наружных поверхностях стенки поддерживаются постоянные температурыt_с1иt_с2. Коэффициент теплопроводности стенки постоянен и равенλ. При стационарном режиме () и отсутствии внутренних источников теплоты (q_v=0) дифференциальное уравнение теплопроводности примет вид:

.

(9.16)

При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки (ось Оx). В этом случае

,

и дифференциальное уравнение теплопроводности перепишется в виде:

.

(9.17)

Граничные условия первого рода запишутся следующим образом: при x=0 t=t_c1; приx=δ t=t_c2. Интегрируя уравнение (9.17), находим

.

После второго интегрирования получаем

.

(9.18)

Постоянные С₁иС₂определим из граничных условий: приx=0 t=t_c1, С₂=t_c1; приx=δ t=t_c2=С₁·δ+t_c1, отсюда 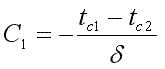. Подставляя значенияС₁иС₂в уравнение (9.18), получим уравнение распределения температуры по толщине стенки:

.

(9.19)

Для определения плотности теплового потока, проходящего через стенку в направлении оси Оx, воспользуемся законом Фурье, согласно которому .

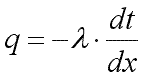Учитывая, что 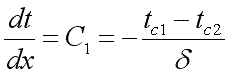, получим

.

(9.20)

Общее количество теплоты, которое передается через поверхность стенки Fза времяτ,

.

(9.21)

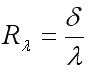Отношение называют тепловой проводимостью стенки, обратную ей величину - термическим сопротивлением теплопроводности. Поскольку величинаλзависит от температуры, в уравнения (9.20), (9.21) необходимо подставить коэффициент теплопроводностиλ_с, взятый при средней температуре стенки.

1
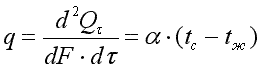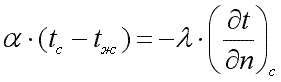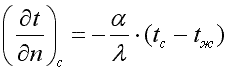
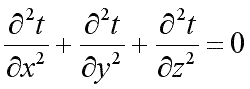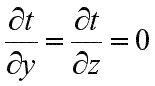
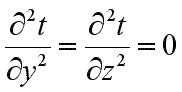
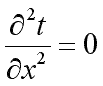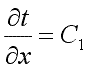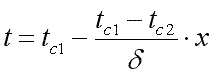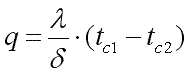