
3-15-1 Мат. модели
.pdf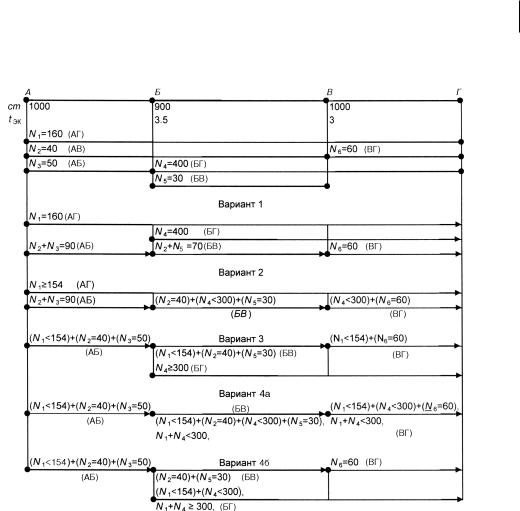
А |
Б |
В |
Г |
|
|
|
|
Рис. 1. Схема полигона АГ и варианты плана формирования поездов
21
P (X ≥ х ) + P (X < х) = 1.
2.2. Аналогично определяем вероятность выделения потока N4 в самостоятельное назначение при N4 ≥ 300:
|
|
|
|
N 4 |
− М (N 4) |
300 − 400 |
|
= |
|||
P (N |
4 |
≥ 300) = 1−Φ |
|
σ(N 4 ) |
|
=1−Φ |
|
|
|||
|
|
||||||||||
|
|
|
|
|
98 |
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
= 1−Φ |
( |
|
) |
= 1 – 0,1539 = 0,8461. |
|
(9) |
|||
|
|
−1,02 |
|
|
|||||||
2.3. Поскольку вагонопотоки N1 и N4 независимы, то вероятность P(A1) события A1 одновременного их выделения в самостоятельное назначение, а, следовательно, что то же самое, вероятность P(A1) выполнения полученного плана формирования поездов (вариант 1, рис. 1) в соответствии с теоремой умножения вероятностей независимых событий будет равна:
b
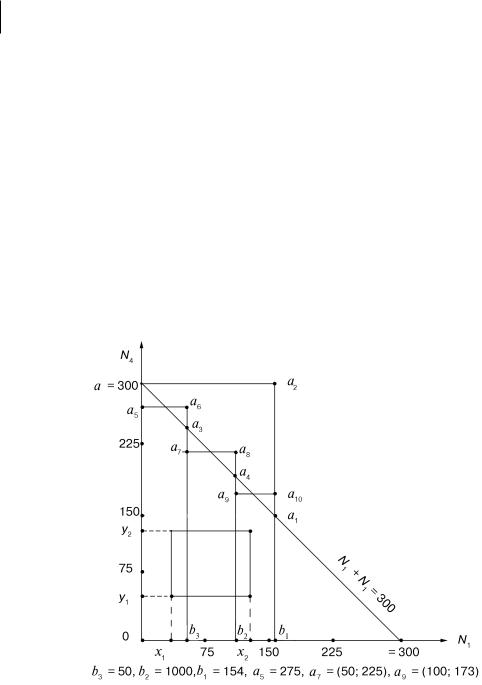
Рис. 2. Определение вероятностей Р(А5) = РВ(А4) и Р(А6) = РB(А4)
22

P(A1) = Р [(N1 ≥ 154) (N4 ≥ 300)] =
=Р (N1 ≥ 154) Р (N4 ≥ 300) = 0,5517 0,8461 = 0,4668.
3.Проанализируем различные варианты плана формирования поездов при случайных событиях
A2 = (N1 ≥ 154, N4 < 300), A3 = (N1 < 154, N4 ≥ 300),
A4 = (N1 ≥ 154, N4 ≥ 300).
Значения N1 = 154 и N4 = 300 назовем критическими.
3.1. Пусть не отвечает необходимому условию вначале более короткое назначение БГ с вагонопотоком N4 при сохранении вагонопотока N1 ≥ 154 по назначению АГ.
Вероятность P (N4 < 300) определена и равна 0,1539. Вероятность P(A2) такого варианта (варианта 2), как вероятность совпадения двух независимых случайных событий N1 ≥ 154 и N4 < 300 определяется в соответствии с теоремой умножения вероятностей независимых событий:
P(A2) = Р [(N1 ≥ 154) (N4 <300)] = Р (N1 ≥ 154)
Р (N4 < 300) = 0,5517 0,1539 = 0,0849.
На рис. 1 представлен вариант 2 плана формирования поездов:
N1 ≥ 154 (АГ), N2 + N4 = 90 (АБ), [(N2 = 40) + (N4 < 300) + (N5 = 30)] (БВ),
[(N4 < 300)+(N5 = 60)] (ВГ).
3.2. Пусть N1 < 154, а N4 ≥ 300, тогда получим вариант 3 (рис.1) плана формирования поездов с вероятностью:
P(A3) = Р [(N1 < 154) (N4 ≥ 300)] = Р (N1< 154)
Р (N4 ≥ 300) = 0,4483 0,8461= 0,3793.
23

В самостоятельное сквозное назначение выделяется только вагонопоток N4 ≥ 300.
Проверим, удовлетворит ли необходимому условию (5) в этом варианте объединение потоков N1 и N2 для формирования сквозного назначения поездов в направлении АВ. Возьмем наибольшее возможное значение, равное критическому N1 = 154, и объединим с N2 = 40:
(N1 =154) +( N2 = 40) =194.
Для объединения N1 и N необходимо, чтобы их сумма была бы не меньше требуемой (условие (5)):
N1 + N2 |
1000 |
= 286. |
||
|
3,5 |
|||
|
|
|||
Но поскольку (N1 =154) + (N2 = 40) =194 < 286, то объединение только вагонопотоков N1 и N2 для формирования сквозного назначения поездов в направлении АВ нецелесообразно. В результате получим вариант 3 плана формирования поездов (рис 1) :
[(N1< 154 ) + (N2 = 40) + (N3 = 50)] (АБ),
[(N1 < 154) + (N2 = 40) +(N5 = 30)] (БВ),
N4 ≥ 300 (БГ),
[(N1 < 154)+(N6 = 60)] (ВГ).
3.3. Пусть оба вагонопотока N1 и N4 одновременно меньше критических значений: N1< 154 и N4 < 300. Вероятность этого события, − вероятность P (A4) получения варианта 4 плана формирования поездов равна:
P (A4) = Р [(N1 < 154) (N4 <300)] = Р (N1 < 154)Р (N4 < 300) = 0 ,4483 0 ,1539 = 0,069.
24

4. Выводы:
4.1. Установлены всевозможные варианты плана формирования поездов, соответствующие следующим случайным событиям и вероятностям их наблюдения:
Вариант 1 A1 = (N1 ≥ 154) (N4 ≥ 300), P(A1) = 0,4668. Вариант 2 A2 = (N1 ≥ 154) ( N4 < 300), P(A2) = 0,0849. Вариант 3 A3 = (N1 <154) (N4 ≥ 300), P(A3) = 0,3793.
Вариант 4 A4 = (N1 <154) ( N4 < 300), P(A4) = 0,069.
События A1, A2, A3, A4 являются несовместными и составляют полную систему событий. На основании теоремы о вероятности суммы событий , составляющих полную систему при суммировании вероятностей событий A1, A2, A3, A4 должны получить 1:
P(A1 + A2 + A3 + A4)= P (A1) + Р (A2 ) + Р (A3 ) + Р (A4 )=
= 0,4668 + 0,0849 + 0,3793 + 0,069 =1,0000.
Полученный результат свидетельствует о правильности выполненного вероятностного анализа плана формирования поездов в соответствии с исходными данными примера.
4.2.Из всех четырех вариантов плана формирования поездов
вариант 1 имеет наибольшую вероятность P (A1 ) = 0,4668. Это означает, что вариант 1 является оптимальным для организации вагонопотоков на полигоне АГ.
4.3.Общее число вариантов плана формирования поездов равно числу событий, определяемых с помощью критических значений вагонопотоков и составляющих полную систему событий, сумма вероятностей которых равна 1. Исходные данные примера предопределили 4 варианта плана формирования поездов.
5. Вариант 4, соответствующий событию A4 , возможен в любом из двух случаев:
1) B = N1+ N4 < 300, что вызывает необходимость расмотрения варианта 4a плана формирования поездов без какоголибо одного сквозного назначения,
25

– ≥
2) B = N1+ N4 300, тогда появляется необходимость рассмотрения варианта 4b плана формирования поездов, в котором будет иметь место одно сквозное назначение БГ.
5.1. Представление варианта 4 в виде двух вариантов дает основание и позволяет в соответствии с законами алгебры событий выразить событие A4 в виде суммы двух несовместных событий A5 и A6 :
A4 = A5 + А6,
где A4 = (N1 < 154) (N4 < 300), A5 = (N1 <154, N4 <300,
N1 + N4 < 300), A6 = (N1 < 154, N4 < 300, N1 + N4 ≥ 300).
Таким образом, вариант A4 представляется одним из вариантов, безразлично каким, либо вариантом 4a (событие A5), либо
вариантом 4b (событие A6 ). При этом A5 |
есть условное событие |
|||||||||||||||
A |
, рассматриваемое при условии B = N |
+ N |
4 |
< 300, т.е. A |
5 |
= |
(A |
). |
||||||||
4 |
|
|
= –(A |
), где |
– |
|
+ N |
1 |
|
|
|
B |
4 |
|
||
Аналогично, A |
6 |
В = N |
1 |
4 |
|
≥ 300. |
|
|
|
|
||||||
|
|
B 4 |
|
|
|
|
|
|
|
|
|
|
|
|||
Используя теорему о вероятности суммы несовместных событий, получим:
P (A4) = Р(A5 + A6) = Р (A5)+ Р (A6 )= Р B (A4) + Р B (A4) ,
где P (A5) = P B (A4), P (A6) = P B (A4) .
5.2. Вероятность P (A4) = 0,069. Однако, при критических значениях вагонопотоков N1 и N4, отличающихся от N1=154 и N4 = 300 и при других параметрах M(N1), σ(N1), M(N4), σ(N4), а также при иных законах распределения вероятностей случайных величин N1 и N4, вероятность P (A4) может оказаться значительно больше, чем P (A4) = 0,069. И тогда появится необходимость определить вероятности P (A5) и P (A6).
6. Рассмотрим вариант 4а и определим вероятность P(A5) = P B (A4) его получения.
26

В силу невыполнения условия (5) при A5 = (N1 < 154, N4 < 300,N1 + N4 < 300) вариант 4а не имеет ни одного сквозного назначения, его график представлен на рис. 1:
|
<154 |
) |
+ |
(N |
2 |
= 40 |
) |
+( |
N 3 |
= 50) |
(АБ),[(N |
1 |
<154) + |
||||||
(N 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
+(N 2 = 40) +(N 4 < 300) +(N 5 = 30)](БВ), |
||||||||||||||||||
|
(N 1 |
<154 |
) |
+ |
(N 4 |
< 300 |
) |
+( |
N |
6 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
= 60) (ВГ). |
|||||||||
Двумерная случайная величина (N1, N4) описывается двумерным нормальным распределением, удовлетворяющим не обходимому и достаточному условию независимости случайных величин N1 и N4. Вероятностную математическую модель события A5 =B(A4) представим вероятностью попадания двумерной случайной точки (N1, N4) в часть области плоскости (0 ≤ N1 ≤ 154, 0 ≤ N4 ≤ 300), ограниченную осями координат ОN1 и ON4 и прямой N1 + N4 =300 в поле трапеции Oaa1b1 (рис. 2) [3]. Очевидно, что при этом выполняются условия получения вари-
анта 4a: N1 < 154, N4 < 300, N1 + N4 < 300.
Условия получения варианта 4b, а именно, N1 <154, N4 <300, N1 + N4 ≥ 300 будут выполнены, если точка (N1, N4 ) попадает в поле треугольника аа2а1 .
Вероятностная математическая модель события A5 =B(A4) предполагает следующий порядок определения вероятности
Р(A5) = РB(A4) [Доп. 2].
6.1. Трапецию Oaa1b1 разобьем на ряд частичных трапеций; чем больше их число, тем точнее будет результат; с целью сокращения объема расчетной работы ограничимся всего лишь тремя частичными трапециями S1 =(Oaa3b3), S 2 =(b3a3a4b2),
S3 =( b2а4а1b1 ).
6.2.Частичные трапеции заменим равными по площади
прямоугольниками S ′ =(Oa |
a |
b |
), S ′ =(b |
a |
a |
b |
), S ′ =(b |
a |
a |
10 |
b |
), |
|||
1 |
5 |
6 |
3 |
2 |
3 |
7 |
8 |
2 |
3 |
2 |
9 |
|
1 |
|
|
что дает основание считать, что и вероятности попадания точки (N1, N4 ) в фигуры трапеций и прямоугольников, равных по площади, также равны.
27

Равенство вероятностей попадания точки (N1, N4 ) в фигуру трапеции и прямоугольника является приближенным в силу «выхода» фигуры прямоугольника в область (N1, N4 ) (N1 <154, N4 <300, N1 + N4 ≥ 300). В связи с этим рекомендуется разбить отрезок [0; b1] на оси O N1 не на три, как показано на рис. 2, а на большее число частичных отрезков.
6.3. Используем выражение для определения вероятно-
сти P попадания точки (N1, |
N4) |
|
в |
|
прямоугольную область |
||||||||||||||||
( х1 ≤ N 1 ≤ x 2, y1 ≤ N 4 ≤ y2 ): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
P[(N 1,N 4) (x1 ≤ N 1 ≤ x 2, y1 ≤ N 4 ≤ y2)] = |
|
||||||||||||||||||||
|
x |
2 |
− M N |
|
|
|
x |
− M N |
|
|
|
|
|
||||||||
Ф |
|
|
( 1 ) |
|
−Ф |
1 |
|
( 1 ) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
σ(N1 ) |
|
|
|
|
|
|
|
σ(N1 ) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(10) |
||||
|
y |
− M N |
4 ) |
|
|
y |
− M N |
4 ) |
|
|
|||||||||||
|
|
||||||||||||||||||||
Ф |
|
2 |
( |
|
−Ф |
|
1 |
( |
, |
|
|||||||||||
|
|
σ(N4 ) |
|
|
|
|
|
σ(N4 ) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где N1 и N4 – нормально распределенные случайные величины, Ф(х) – функция распределения стандартной нормальной случайной величины N (х,0;1) (функция Лапласа).
При выполнении расчетов:
1)используется таблица значений функции Лапласа Ф(х), приведенная в приложении 3,
2)необходимо иметь ввиду свойство функции Ф(х):
Ф(– х) = 1–Ф( х) , 3) функцию Лапласа Ф(х) можно заменить нормированной
функцией Лапласа Ф0 (х )
|
1 |
x |
− |
t2 |
||
Ф0 (x )= |
∫0 e |
|
dt = Ф(х )− 0,5, |
|||
2 |
||||||
2π |
|
|||||
таблица значений которой приводится в приложении 2.
28

Например: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
2 |
− М N |
1 ) |
|
|
х − М N |
1 ) |
|
|
|||
Ф |
|
( |
|
−Ф |
1 |
( |
|
= |
|||||
|
|
σ(N1 ) |
|
|
|
σ(N1 ) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
х |
2 |
− М N |
1 ) |
|
|
|
х − М N |
1 ) |
|
|||
= Ф0 |
|
|
( |
|
−Ф0 |
|
1 |
( |
. |
|||||
|
|
σ(N1 ) |
|
|
|
σ(N1 ) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Однако, при этом надо иметь ввиду свойство нечетности функции Ф0 (х ) т.е. Ф0 (−х )= −Ф0 (х ).
6.4 С помощью выражения (10) определяем вероятности |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
попадания случайной точки (N1,N4 ) в поле прямоугольников |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S′1, S′2, S′3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
− М N |
1 ) |
|
|
|
|
|
|
0 − М N |
1 ) |
|
|
|
|||||||||||||||||||||
|
P |
(N1,N |
4 ) S′1 = Ф |
|
|
3 |
|
|
|
( |
|
|
− |
Ф |
|
|
|
|
|
( |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
σ(N1 ) |
|
|
|
|
|
|
σ(N1 ) |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
a |
|
− М N |
4 ) |
|
|
|
|
0 |
− |
М N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
Ф |
|
5 |
|
|
|
|
( |
|
|
−Ф |
|
|
|
|
|
|
|
( |
4 ) |
|
= |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
σ(N4 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ(N4 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
50 |
−160 |
|
|
|
|
|
|
0 |
−160 |
|
|
|
275 − 400 |
|
|
0 |
− 400 |
|
||||||||||||||||||||||||||||||||||||
= |
Ф |
|
|
|
|
|
|
|
−Ф |
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
−Ф |
|
|
|
|
|
|
|
= |
|||||||||||||||
|
46 |
|
|
|
|
|
|
|
|
|
|
|
|
98 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
) |
|
46 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
98 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|||||
|
|
|
= Ф |
−2,39 |
|
−Ф −3,48 |
|
|
Ф(−1,28) −Ф |
−4,08 |
= |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
= |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) ( |
|
|
|
|
|
|
|
) |
= 0,0008. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
0,0082 − 0,0002 |
|
|
0,1003 − 0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
− М N |
|
|
|
|
|
b |
− |
М N |
1 ) |
|
|
|
||||||||||||||||||||
|
Р |
(N1,N |
4 ) S2′ |
= |
Ф |
|
2 |
|
|
|
( |
1 ) |
− |
Ф |
|
|
3 |
|
|
( |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ(N1 ) |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ(N1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
a |
|
− М N |
4 ) |
|
|
|
|
0 − М N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
Ф |
|
7 |
|
|
|
|
( |
|
|
−Ф |
|
|
|
|
|
|
|
( |
4 ) |
|
= |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
σ(N4 ) |
|
|
|
|
|
|
|
σ(N4 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
100 −160 |
|
|
|
|
|
|
50 −160 |
|
|
|
|
|
225 − |
400 |
|
0 − 400 |
|
||||||||||||||||||||||||||||||||||||||
= Ф |
|
|
|
|
|
|
|
|
−Ф |
|
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
− Φ |
|
|
|
|
|
|
|
|
= |
|||||||||||||
46 |
|
|
|
|
46 |
|
|
|
|
|
|
|
|
98 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
98 |
|
|||||||||||||||||||||||||
|
|
|
|
|
( |
|
|
|
|
−Ф |
( |
|
|
|
|
) |
|
( |
|
|
|
|
|
) |
−Ф |
( |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
= Ф −1,3 |
|
|
|
|
−2,39 |
|
|
|
|
Ф |
|
−1,79 |
|
|
|
|
−4,08 |
|
= |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
= |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) ( |
|
|
|
|
|
|
|
) |
= 0,0033. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
0,0968 − 0,0082 |
|
|
0,0367 − 0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
29

|
|
|
|
|
|
|
|
|
|
b − М N |
|
|
|
|
b − М N |
1 ) |
|
|
|
||||||||||||
|
Р (N1,N |
4 ) S3′ |
|
= Ф |
1 |
|
|
( |
|
1 ) |
− |
Ф |
2 |
( |
|
|
|
||||||||||||||
|
|
|
σ(N1 ) |
|
|
|
σ(N1 ) |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
− М N |
4 ) |
|
0 |
− М N |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Ф |
|
9 |
|
|
( |
− |
Ф |
|
|
|
|
|
( 4 ) |
= |
|
|
|
|
|
|
|||||||||
|
|
|
σ(N4 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
σ(N4 ) |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
154 −160 |
|
|
|
|
100 −160 |
|
|
173 − 400 |
0 |
− 400 |
|
|||||||||||||||||||
= Ф |
|
|
|
− |
Ф |
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
− Φ |
|
|
|
|
|
|
= |
||||
|
|
|
46 |
|
|
|
|
98 |
|
|
98 |
|
|||||||||||||||||||
|
46 |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
( |
|
|
|
|
( |
) |
( |
|
|
|
|
) |
|
( |
) |
|
|
|
|
|
|
||||||||
|
|
= Ф |
−0,13 |
|
− Ф |
−1,3 Ф −2,32 |
|
|
− Ф −4,08 = |
|
|
|
|
||||||||||||||||||
=(0,4483 − 0,0968) (0,0102 − 0)= 0,0036.
6.5.Вероятность Р(A5) = РB(A4) определяется суммой:
|
|
3 |
|
|
S′ |
|
|
P( |
) = |
∑ |
P N |
,N |
= 0,0008 + 0,0033 + 0,0036 = 0,0077. |
||
|
A5 |
( 1 |
|
4 ) |
i |
|
|
|
|
i =1 |
|
|
|
|
|
7. Рассмотрим вариант 4b и определим вероятность Р(A6 ) =
= Р–(A ) его получения.
B 4
Случайному событию А4 =(N1 < 154, N4 < 300) соответствует попадание двумерной случайной точки (N1, N4) в поле прямоугольника (Oaa2b1) (рис. 2) с вероятностью:
|
|
|
P (A4 )= P (0 < N1 <154) P (0 < N4 < 300)= |
|
|
|
|||||||||||||||||||||||||||||||
|
154 |
−160 |
|
|
|
|
|
|
0 |
−160 |
|
|
|
300 − 400 |
|
|
|
0 − 400 |
|
||||||||||||||||||
= Ф0 |
|
|
|
|
|
|
|
− Ф0 |
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
− Ф0 |
|
|
= |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
98 |
|
|
|||||||||||||||||||||||
|
46 |
|
|
|
|
|
) |
|
|
|
|
|
|
|
46 |
|
|
|
|
|
|
|
( |
|
98 |
|
|||||||||||
|
|
|
0 ( |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
( |
|
|
) |
− Ф |
0 |
|
) |
|
||||||||
|
= Ф |
−0,13 |
|
− Ф |
(−3,48) |
Ф |
|
|
−1,02 |
) |
|
−4,08 = |
|
||||||||||||||||||||||||
|
|
|
|
0 |
( |
|
|
|
|
) |
+ |
Ф |
0 |
( |
|
) |
Ф0 |
( |
|
+ Ф |
0 |
( |
|
) |
|
||||||||||||
|
= −Ф |
|
0,13 |
|
|
3,48 |
|
− |
|
|
|
1,02 |
|
|
4,08 |
= |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
) |
= 0,069. |
|
|
|||
|
= (−0,05172 + 0,49977) −0,34614 + 0,49997 |
|
|
|
|||||||||||||||||||||||||||||||||
Поскольку A |
4 |
= |
B |
(A |
|
) + –(A |
), где |
B |
(A |
) и –(A ) несовместные |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
B |
4 |
|
|
|
|
|
4 |
|
|
B |
4 |
|
|
|
|
|
||||||||
события, то по теореме о вероятности суммы несовместных событий имеем
30
