3. Средние величины

3.1. Сущность средних величин, правила их применения

Средняя величина в статистике –обобщающий показатель, характеризующий типичное для данной совокупности значение признака или соотношение между признаками в определенных условиях места и времени действия.

Признак, среднее значение которого определяется, называется осредняемым (усредняемым) признаком. Отдельные значения осредняемого признака обозначаются Х_i.

Числа, характеризующие количество повторений данного значения признака, называются частотами (f_i).

Средние величины должны вычисляться для:

1. Качественно однородных совокупностей;

2. Массовых явлений (только в массовых явлениях в силу действия закона больших чисел взаимно исключаются индивидуальные значения, действие случайных факторов и проявляются типичные размеры);

3. Средняя, вычисленная для совокупности в целом, (общая средняя) должна дополняться средними, рассчитанными для отдельных групп этой совокупности (групповыми средними), а в ряде случаев, индивидуальными значениями признака, как правило, максимальным и минимальным, чтобы не потерять передовое и отстающее.

2. Виды средних величин, способы их расчета и условия применения

1. Средняя арифметическая простая

n – количество единиц в совокупности, для которой вычисляется средняя величина.

Средняя арифметическая простая применяется для несгруппированных данных, когда известны отдельные значения осредняемого признака.

2. Средняя арифметическая взвешенная

Средняя арифметическая взвешенная применяется для сгруппированных данных, когда известны отдельные значения осредняемого признака (х_i) и количество повторений соответствующего значения признака (f_i).

3. Средняя гармоническая взвешенная

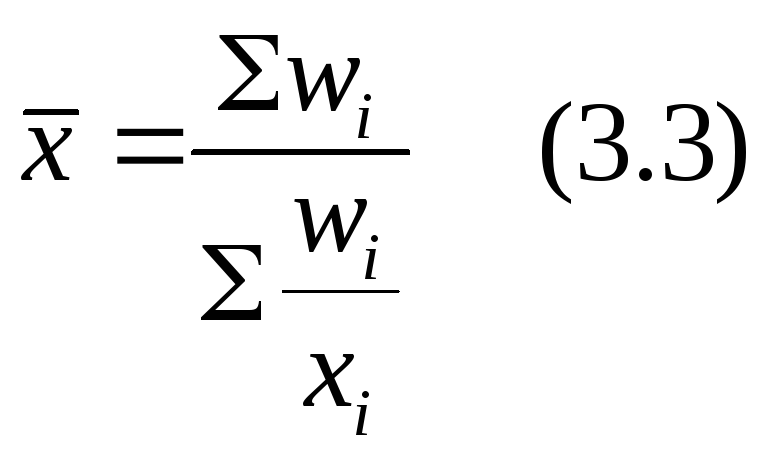
W_i – общее значение осредняемого признака в i-ой группе.

Средняя гармоническая взвешенная применяется для сгруппированных данных, когда известны отдельные значения осредняемого признака (х_i) и общие значения осредняемого признака в группах (w_i).

4. Средняя гармоническая простая

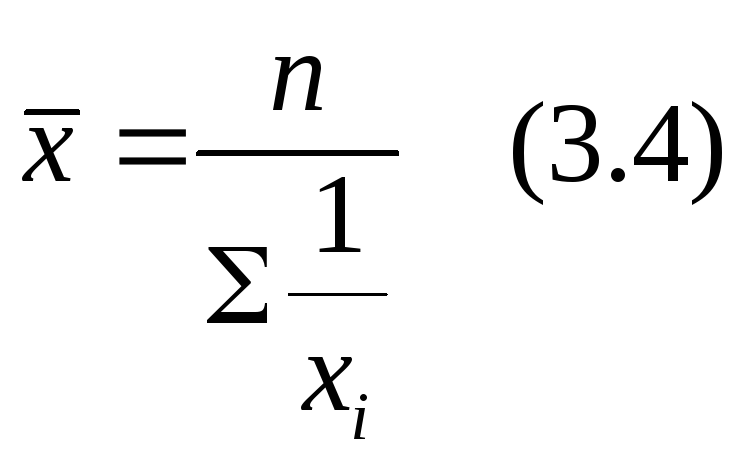
Средняя гармоническая простая применяется для сгруппированных данных, когда известны отдельные значения осредняемого признака (х_i) и общие значения осредняемого признака в группах (w_i), причем

w₁ = w₂ =…= w_i =…= w_n-1 = w_n .

5. Агрегатная средняя

Агрегатная средняя применяется для сгруппированных данных, когда известны общие значения осредняемого признака в группах (w_i) и количество повторений соответствующего значения признака (f_i).

Виды средних 1 – 5 применяются когда общее значение осредняемого признака можно определить как сумму отдельных его значений.

6. Средняя геометрическая простая

(3.6)

Средняя геометрическая применяется, когда общее значение осредняемого признака можно определить как произведение отдельных его значений.

- символ произведения.

7. Средняя геометрическая взвешенная

(3.7)

Степенная средняя простая

(3.8)

При

k = -1 – средняя гармоническая простая

k = 1 – средняя арифметическая простая

k = 2 – средняя квадратическая простая

Степенная средняя взвешенная

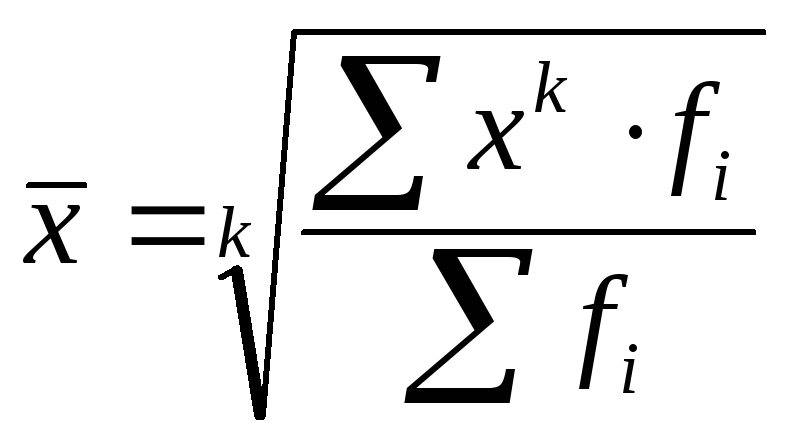(3.9)

При

k = -1 – средняя гармоническая взвешенная

k = 1 – средняя арифметическая взвешенная

k = 2 – средняя квадратическая взвешенная

Правило мажорантности средних: чем больше степень, тем больше средняя величина.

3. Свойства средней арифметической:

1. При изменении всех значений признака в равное число раз, средняя изменится во столько же раз.

2. Если изменить все значения осредняемого признака на постоянную величину «С», средняя изменится на эту же величину.

3. При изменении всех значений частот в равное число раз, средняя не изменится.

Если принять в качестве постоянной величины , то

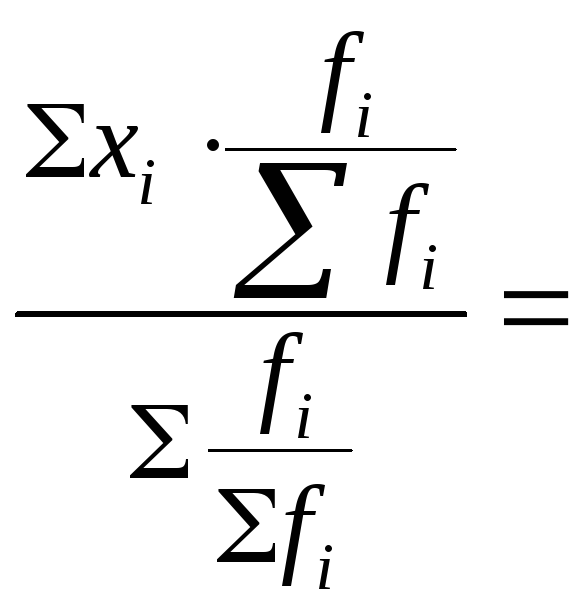
- модель средней

4. Произведение средней величины на сумму всех частот равно общему значению осредняемого признака.

5. Сумма отклонений значений признака от средней величины равна нулю.

3.4. Расчет средней в вариационных рядах

Вариационный ряд состоит из двух элементов: вариантов и частот (частостей), следовательно, средняя в вариационных рядах вычисляется по формуле средней арифметической взвешенной:

, где

х_i - i – е значение признака (варианта);

f_i – значение частоты у i – го значения признака;

df_i – частость

В интервальных вариационных рядах среднее значение вычисляется условно на середину интервала. Величина открытого интервала принимается равной величине соседнего с ним интервала.

В интервальных рядах с равными интервалами среднее значение признака можно вычислить способом моментов. Данный способ основан на свойствах средней арифметической и состоит из следующих этапов:

1. Из всех значений признака вычитается постоянная величина «С», равная одному из значений середин интервалов, как правило, расположенное в центре ряда и (или) обладающее максимальной частотой (частостью);

2. Полученные значения делят на величину интервала (Δi). Преобразованные значения середин интервалов обозначим

Независимо от величины интервала, значений середин интервала всегда получают следующий ряд:

-2 -1 0 +1 +2 +3

Точка отсчета () равна 0, каждое последующее значение отличается от предыдущего на 1.

3. Вычисляется средняя величина из преобразованных значений середин интервалов. Данная средняя называется моментом первого порядка (m₁).

4. На основе момента первого порядка вычисляют среднюю величину.

Структурные средние

Мода – наиболее распространенное значение признака.

В дискретных вариационных рядах устанавливается максимальное значение частоты (частости). Значение признака, соответствующее данной частоте (частости) и является модой.

В интервальных вариационных рядах с равными интервалами максимальной частоте (частости) соответствует модальный интервал. Конкретное значение моды вычисляется по формуле:

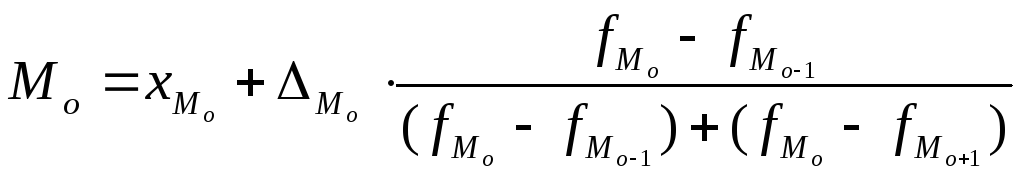, где

М_о – мода;

ХМо – нижняя (минимальная) граница модального интервала;

ΔМо – величина модального интервала;

fМо – частота модального интервала;

fМо-1 - частота интервала, предшествующего модальному;

fМо+1 - частота интервала, следующего за модальным.

В интервальных вариационных рядах с неравными интервалами модальный интервал и значение моды вычисляется на основе плотности распределения. Конкретное значение моды вычисляется по формуле:

, где

М_о – мода;

ХМо – нижняя (минимальная) граница модального интервала интервала с максимальной плотностью распределения;

ΔМо – величина модального интервала;

ρМо – плотность модального интервала;

ρМо-1 – плотность интервала, предшествующая модальному интервалу;

ρМо+1 – плотность интервала, следующая за модальным интервалом.

Структурные средние можно определить графическим путем.

Для ряда с равными интервалами моду определяют на основе гистограммы распределения.

Рис. 4,1

Определение моды

Для ряда с неравными интервалами моду определяют на основе плотности распределения аналогично.

Медиана - значение признака, которое делит численность упорядоченного ряда на две равные части. Для расчета медианы в вариационных рядах:

1. Определяется порядковый номер медианы

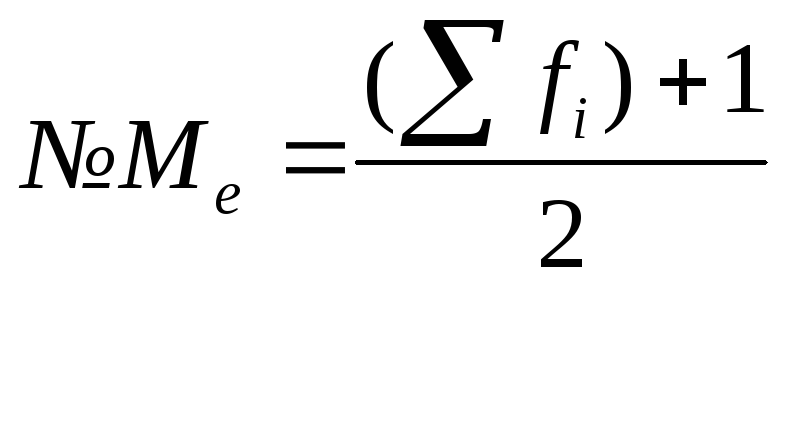, где

- объем ряда

2. Вычисляется сумма накопленных частот (кумулятивная сумма) – Si

3. Находится такое значение Si, которое первым будет равно или больше порядкового номера медианы

4. В дискретных вариационных рядах этой сумме соответствует медиана, в интервальных рядах – медианный интервал

5. Для интервального вариационного ряда конкретное значение медианы вычисляется по формуле:

,где

- медиана

- нижняя (минимальная) граница медианного интервала

- величина медианного интервала

fМе – частота медианного интервала

SM_е-1 - сумма накопленных частот до медианного интервала

Аналогично вычисляют квартили, децили …

Порядковый номер 3-го дециля равен

В интервальных вариационных рядах конкретное значение третьего дециля вычисляется по формуле:

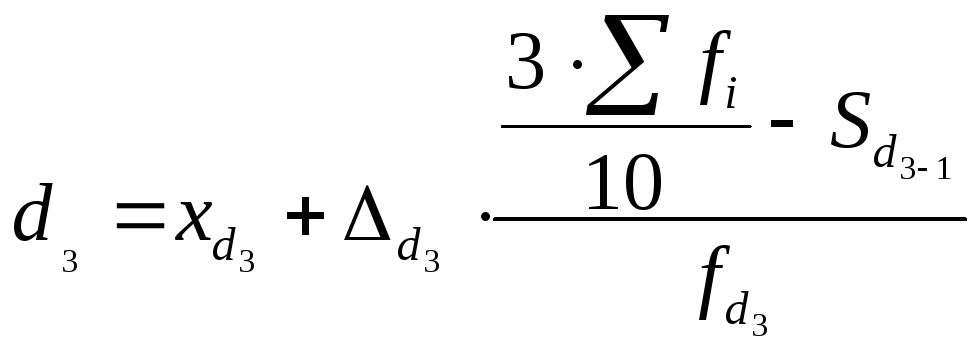, где

- 3-ий дециль

- нижняя граница 3-го децильного интервала

- величина 3-го децильного интервала

Sd3-1 - сумма накопленных частот до 3-го децильного интервала

fd3 - частота 3-го децильного интервала

Графически в вариационных рядах медиану, квартили, децили, … можно определить на основе кумуляты распределения.

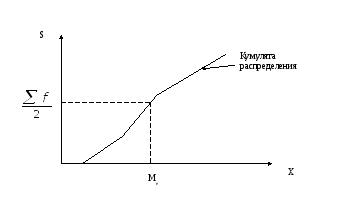
Рис. 4.2

Определение медианы