
лекции строймех
.pdf
А.А. КРАМАРЕНКО Л.А. ШИРОКИХ
ЛЕКЦИИ
ПО СТРОИТЕЛЬНОЙ МЕХАНИКЕ СТЕРЖНЕВЫХ СИСТЕМ
ЧАСТЬ 3
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
МЕТОД СИЛ
НОВОСИБИРСК 2002
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
А.А. Крамаренко, Л.А. Широких
ЛЕКЦИИ
ПО СТРОИТЕЛЬНОЙ МЕХАНИКЕ СТЕРЖНЕВЫХ СИСТЕМ
ЧАСТЬ 3
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
МЕТОД СИЛ
НОВОСИБИРСК 2002
УДК |
624.041.1 |
ББК |
38.112 |
К |
777 |
Крамаренко А.А.
ЛЕКЦИИ ПО СТРОИТЕЛЬНОЙ МЕХАНИКЕ СТЕРЖНЕВЫХ СИСТЕМ. Ч. 3. СТАТИ- ЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ. МЕТОД СИЛ / А.А. Крамаренко,
Л.А. Широких. – Новосибирск: НГАСУ, 2002. – 144 с.

ISBN–5-7795-0093-2
В третью часть настоящего учебного издания включено шесть лекций, посвящённых определению перемещений в статически определимых системах в матричной форме, теоремам взаимности строительной механики, общей характеристике и расчёту статически неопределимых систем методом сил на силовые, температурные и кинематические воздействия.
Лекции разработаны для студентов безотрывных форм обучения в соответствии с требованиями государственного стандарта высшего профессионального образования к обязательному минимуму содержания и уровню подготовки бакалавров по направлению 550100 "Строительство" и инженеров по специальностям 290300 "Промышленное и гражданское строительство", 290400 "Гидротехническое строительство", 290500 "Городское строительство и хозяйство", 291400 "Проектирование зданий". Отдельные лекции и параграфы могут быть рекомендованыстудентам других специальностей направления "Строительство".
Компьютерный набор выполнен инженером А.И. Боевой
Печатается по решению издательско-библиотечного совета НГАСУ
Рецензенты:
В.А. Шутов, д.т.н., профессор, завкафедрой общетехнических дисциплин (НГАХА);
В.К. Фёдоров, к.т.н., профессор кафедры инженерной геологии, оснований и фундаментов (НГАСУ)
ISBN–5-7795-0093-2 © НГАСУ, 2002
©Крамаренко А.А., Широких Л.А., 2002
Учебное издание Крамаренко Анатолий Алексеевич Широких Людмила Алексеевна
ЛЕКЦИИ ПО СТРОИТЕЛЬНОЙ МЕХАНИКЕ СТЕРЖНЕВЫХ СИСТЕМ
ЧАСТЬ 3
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ МЕТОД СИЛ
Темплан 2002 г.
Редактор Г.К. Найдёнова
Санитарно-эпидемиологическое заключение № 54.НЦ. 02.953.П.127.10.01 от 01.10.2001 г.
Подписано к печати 22.10.2002. Формат 60х84 1/16 д.л. Гарнитура Таймс. Бумага газетная. Ризография.
Объём 8,4 уч.-изд.л.; 9,25 п.л. Тираж 250 экз. Заказ №
Новосибирский государственный архитектурностроительный университет
630008, Новосибирск, ул. Ленинградская, 113
Отпечатано мастерской оперативной полиграфии НГАСУ

ОГЛАВЛЕНИЕ |
|
Лекция тринадцатая. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В |
|
МАТРИЧНОЙ ФОРМЕ ...................................... |
4 |
Лекция четырнадцатая. ОБЩИЕ СВЕДЕНИЯ О СТАТИЧЕСКИ |
|
НЕОПРЕДЕЛИМЫХ СИСТЕМАХ................ |
41 |
Лекция пятнадцатая. ТЕОРЕМЫ ВЗАИМНОСТИ |
|
СТРОИТЕЛЬНОЙ МЕХАНИКИ.................... |
50 |
Лекция шестнадцатая. РАСЧЁТ СТАТИЧЕСКИ |
|
НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ |
|
СИЛ НА СИЛОВОЕ ВОЗДЕЙСТВИЕ........... |
59 |
Лекция семнадцатая. РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ СИЛ НА ТЕМПЕРАТУРНОЕ И КИНЕМАТИЧЕСКОЕ ВОЗДЕЙСТВИЕ .98
Лекция восемнадцатая. УЧЁТ СИММЕТРИИ СТАТИЧЕСКИ |
|
НЕОПРЕДЕЛИМЫХ СООРУЖЕНИЙ ПРИ |
|
ИХ РАСЧЁТЕ МЕТОДОМ СИЛ................ |
134 |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК................................................ |
144 |
ЛЕКЦИЯ ТРИНАДЦАТАЯ
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В МАТРИЧНОЙ ФОРМЕ
13.1.Понятие о матрице перемещений
13.2.Вычисление интегралов формулы Мора в матричной форме в случае произвольных подынтегральных функций
13.3.Вычисление интегралов формулы Мора в матричной форме в случае линейных подынтегральных функций Фik(s), ФFk(s)
13.4.Определение перемещений от силового воздействия
13.5.Определение перемещений от температурных воздействий
13.6.Определение перемещений от кинематических воздействий
13.7.Определение перемещений от воздействий различного характера
13.8.Вопросы для самопроверки
13.9.Рекомендуемая литература
13.1.Понятие о матрице перемещений
В инженерных расчётах часто возникает необходимость определения группы различных перемещений узлов и сечений заданного сооружения от независимых друг от друга внешних воздействий – силовых, температурных, кинематических. Таблица величин этих перемещений, составленная по определенным правилам, называется матрицей перемещений.
Например, в раме, показанной на рис. 13.1, требуется определить горизонтальное перемещение узла А, вертикальное перемещение сечения "к" и угол поворота сечения "а" отдельно от равномерно распределенной нагрузки q, сосредоточенной силы F, сосредоточенного момента М, изменения температуры
t1o , to2 , t3o и смещения опорных связей (1), (2). Установим следующий порядок формирования матрицы перемещений. В её
3 |
4 |

первой строке будем фиксировать только величины горизонтального перемещения узла А, во второй
– вертикального перемещения сечения "к", в третьей – угла поворота сечения "а". По-
рядок записи величин искомых перемещений в каждой строке зависит от принятой нумерации внешних воздействий. Для нашего примера примем: первое воздействие – равномерно распределённая нагрузка q, второе – сосредоточенная сила F, третье – сосре-
доточенный момент |
|
М, четвёртое – изменение температуры |
|||||
t1o , to2 , t3o , пятое – |
смещение опорных связей (1), (2). С учё- |
||||||
том установленных правил получим матрицу перемещений |
|||||||
|
|
(q) |
(F) |
(M) |
(t) |
(c) |
|
= |
|
Ax |
Ax |
Ax |
Ax |
Ax |
|
|
(q) |
(F) |
(M) |
(t) |
(c) . |
||
|
|
ky |
ky |
ky |
ky |
ky |
|
|
|
θ(q) |
θ(F) |
θ(M) |
θ(t) |
θ(c) |
|
|
|
a |
a |
a |
a |
a |
|
Вобщем случае для любой задачи число строк матрицы перемещений равно числу определяемых перемещений различного характера, а число столбцов – числу независимых внешних воздействий (собственный вес конструкций, снег, ветер, технологическая нагрузка, изменение температуры, смещение опорных связей и т.д.). В первом столбце матрицы перемещений принято записывать группу искомых перемещений от постоянной нагрузки.
Внастоящей лекции рассматривается вычисление элементов матриц перемещений в матричной форме. Для успешного усвоения материала этой и последующих лекций читателям полезно повторить некоторые разделы линейной алгебры, связанные с действиями транспонирования, сложения, вычитания, умножения
иобращения матриц.
13.2. Вычисление интегралов формулы Мора в матричной форме в случае произвольных подынтегральных функций
В одиннадцатой лекции (см. Крамаренко А.А. Лекции по строительной механике стержневых систем. Ч. 2. Статически определимые системы: Курс лекций / А.А. Крамаренко. – Новосибирск: НГАСУ, 2002. – п. 11.4) было отмечено, что определённые интегралы всех членов формулы Мора
nM lk Mik (s)MFk (s)ds |
nQ lk |
Qik (s)QFk (s)ds |
+ |
|
jk = ∑ ∫ |
EJk (s) |
+ ∑ ∫ k τk |
GAk (s) |
|
k=1 0 |
k=1 0 |
|
||
|
nN lk Nik (s)NFk (s)ds |
|
||
|
+ ∑ ∫ |
EAk (s) |
|
|
|
k=1 0 |
|
|
|
имеют одинаковую структуру и в обобщённой форме могут быть представлены следующим образом:
lk Φ |
ik |
(s)Φ |
Fk |
(s)ds |
. |
(13.1) |
|
∫ |
|
|
|
||||
|
|
Tk (s) |
|
||||
0 |
|
|
|
|
|
||
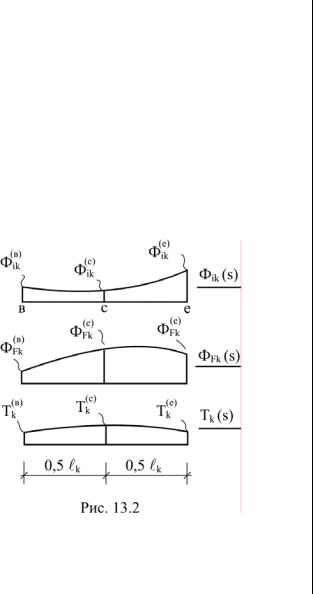
Здесь Фik(s) – общее представление функций внутренних усилий Мik(s), Qik(s), Nik(s) от единичного фактора, приложенного в направлении определяемого перемещения; ФFk(s) – представление функций внутренних усилий МFk(s), QFk(s), NFk(s) от заданного силового воздействия; Tk(s) – представление функций, описывающих изменение жесткостей поперечных сечений EJk(s), GAk(s), EAk(s) и параметра kτk вдоль оси k-го грузового участка.
Численное значение определённого интеграла (13.1) можно получить по формуле Симпсона в матричной форме
l |
k Φ |
|
(s)Φ |
|
(s)ds |
|
l |
|
|
Φ |
(в) |
Φ |
(в) |
Φ |
(с) |
Φ |
(с) |
|
Φ |
(е) |
Φ |
(е) |
|
|||||
|
ik |
Fk |
|
k |
|
|
Fk |
|
ik |
|
Fk |
|
|
|
Fk |
|
|
|||||||||||
∫ |
|
|
|
= |
|
|
|
ik |
+ 4 |
|
|
+ |
ik |
|
|
= |
||||||||||||
|
|
Tk (s) |
|
6 |
|
(в) |
|
|
T |
(с) |
|
|
(е) |
|
||||||||||||||
0 |
|
|
|
|
|
|
T |
|
|
|
|
k |
|
|
|
T |
k |
|
|
(13.2) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
= ΦТ P |
Φ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
ik |
k Fk |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В соотношении (13.2):
5 |
6 |
|
|
|
|
Φ(в) |
; ΦТ = [Φ(в) Φ(с) Φ(е) ]; |
|
|
|
|
|
Φ(в) |
|
|||||||||||||||||||
|
|
|
|
|
|
ik |
|
|
|
|
|
|
|
|
Fk |
|
|||||||||||||||
Φ |
ik |
= |
Φ(с) |
Φ |
Fk |
= Φ(с) |
; |
||||||||||||||||||||||||
|
|
|
|
|
ik |
|
|
|
ik |
|
|
ik |
|
ik |
|
ik |
|
|
|
|
|
|
Fk |
|
|
||||||
|
|
|
|
Φ(е) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Φ(е) |
|
|||||||
|
|
|
|
|
|
ik |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fk |
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
T0 |
|
0 |
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
T(в) |
|
|
|
|
|
|
|
|
|
T(в) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
l |
k |
|
|
k |
|
4 |
|
|
|
|
|
l |
k |
|
k |
|
T |
|
|
|
|
|
|
|
|
|||
Pk = |
|
|
|
0 |
|
|
|
0 |
|
|
= |
|
|
0 4 |
|
0 |
|
0 |
|
|
; |
|
|||||||||
6 |
|
|
|
T(c) |
|
6T |
T(c) |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
0 |
|
|
|
|
|
k |
|
|
T |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
T(e) |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
(e) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
||||
ΦikT – матрица, транспонированная по отношению к матрице Фik;
Φik(в) , Φ(Fkв) , Tk(в) – значе-
ние функций, входящих в подынтегральное выражение (13.1) в начале ин-
тервала; Φik(c) , Φ(Fkc) , Tk(c) –
в середине; Φik(e) , Φ(e)Fk ,
T(e) – в конце интервала
k
(рис. 13.2); Т0 – некото-
рое произвольное число. Матричная трактовка формулы Симпсона
(13.2) позволяет вычислить перемещения от силового воздействия с любой предварительно заданной точностью.
В частном случае, когда Tk(s) = const = Tk, соотношение (13.2) перепишется:
1 |
l |
lk |
(Φ(в)Φ(в) |
|
||
∫kΦik (s)ΦFk (s)ds = |
+ 4Φ(с)Φ(с) |
|||||
Tk |
6T0 |
|||||
0 |
ik |
Fk |
ik Fk |
|||
|
|
|
||||
|
|
= ΦT P Φ . |
||||
|
|
|
ik k |
Fk |
|
|
Так как Tk(в) = Tk(с) = Tk(е) = Tk , то приняв Т0 = получим:
|
|
lk |
1 0 |
0 |
||
P |
= |
0 |
4 |
0 . |
||
6T |
||||||
k |
|
|
|
|
||
|
|
k |
0 |
|
||
|
|
|
0 |
1 |
||
+Φ(е)Φ(е) )=
ik Fk (13.3)
Тk, в этом случае
Значение определённого интеграла (13.3) будет точным, если подынтегральная функция будет представлять собой алгебраический полином степени не выше третьей (например, когда определяются линейные и угловые перемещения отдельных сечений и узлов стержневых систем от силового воздействия, включающего сосредоточенные силы и моменты, а также равномерно распределённые нагрузки). Если же силовое воздействие содержит распределённые нагрузки с переменными интенсивностями, то матричная формулировка формулы Симпсона и в случае, когда Tk(s) = const даёт приближённое значение определённого интеграла
(13.3).
13.3. Вычисление интегралов формулы Мора в матричной форме в случае линейных подынтегральных функций Фik(s), ФFk(s)
В п. 13.2 упоминалось, что численное значение определённого интеграла (13.1) можно получить в матричной форме (13.2)
|
|
|
lk Φ |
ik |
(s)Φ |
Fk |
(s)ds |
= ΦТ |
P |
Φ . |
|
|||
|
|
|
∫ |
|
|
|
|
|
||||||
|
|
|
|
|
|
Tk (s) |
|
|
||||||
|
|
|
0 |
|
|
|
|
ik |
k |
Fk |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
Учитывая линейность функций Фik(s) и ФFk(s), их значения |
|||||||||||||
при s = 0,5ℓk |
Φ(c) |
и Φ(c) |
выразим через Φ(в) |
и Φ(в) |
при s = 0 и |
|||||||||
|
|
ik |
|
|
Fk |
|
|
|
|
|
ik |
Fk |
|
|
Φ(е) |
и Φ(е) |
при s = ℓk (рис. 13.3). |
|
|
|
|
|
|||||||
ik |
Fk |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
8 |
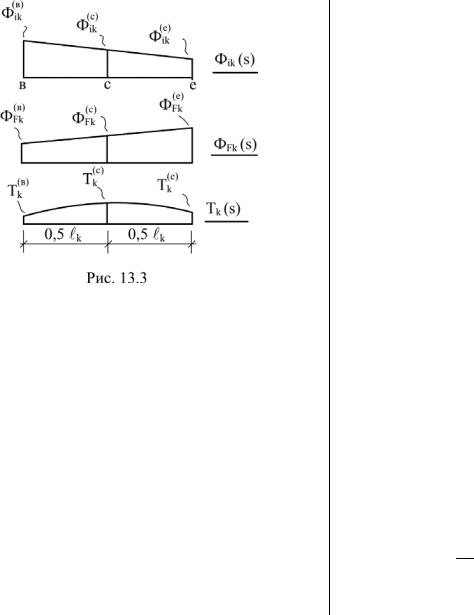
Φik(c) = 0,5(Φik(в) +Φik(е) );
(Fk = ) (13.4)
=0,5 Φ(Fkв) +Φ(Fkе) .
Сучётом зависимостей (13.4) матрицыΦ(c)
выражения (13.2) ΦikT
иФFk перепишутся:
ΦikT = [Φik(в) Φik(c) Φik(e) ]=
1 |
0,5 |
= [Φik(в) Φik(e) ] |
0,5 |
0 |
Φ(Fkв)
ΦFk = Φ(Fkc) =
Φ(e)Fk
1 |
0 |
Φ(Fkв) |
|||
|
|
|
|
||
0,5 |
0,5 |
|
(e) |
||
|
0 |
1 |
|
ΦFk |
|
|
|
|
|
||
0
1 ;
. (13.5)
Принимая во внимание соотношения (13.5), определённый интеграл выражения (13.2) в матричной форме представим следующим образом:
|
|
|
|
lk Φik (s)ΦFk (s)ds |
= |
|
|
|
|
|
||||||||
|
|
|
|
|
∫ |
|
Tk (s) |
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
T0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
(в) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0 |
|
|
|||
|
|
1 |
0,5 |
0 |
|
lk |
Tk |
T0 |
|
|
|
(в) |
|
|||||
(в) |
(e) |
|
|
|
|
|
|
|
|
|
ΦFk |
|||||||
= [Φik |
Φik |
] 0 |
0,5 |
1 |
|
|
|
0 4 |
|
|
0 |
|
0,5 |
0,5 |
Φ(e) |
. |
||
|
6T |
T |
(c) |
|||||||||||||||
|
|
|
|
|
0 |
|
|
|
k |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fk |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
T0 |
0 |
1 |
|
|
||
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T(e) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
Вычислив произведение трёх центральных матриц, получим:
lk Φ |
ik |
(s)Φ |
Fk |
(s)ds |
= |
|
∫ |
|
|
|
|||
|
|
Tk (s) |
|
|||
0 |
|
|
|
|
||
|
|
|
|
|
|
T |
|
|
T |
|||
|
|
|
|
|
|
|
0 |
+ |
|
|
0 |
|
|
|
|
l |
|
|
(в) |
T |
(c) |
||||
(в) |
(e) |
|
k |
T |
k |
|
|
k |
||||
= [Φik |
Φik |
] |
6T |
|
|
|
T0 |
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(c) |
|
||
|
|
|
|
|
|
|
|
Tk |
|
|
|
|
В формуле (13.6):
|
|
T0 |
|
|
|
|
|
|
(13.6) |
|
|
|
|
|
|
Φ(в) |
|
||
|
T(c) |
|
|||||||
|
|
|
|
||||||
T |
|
k |
T |
|
|
Fk |
= ΦT P Φ . |
||
|
|
Φ(e) |
ik k |
Fk |
|||||
0 |
|
+ |
0 |
|
|
Fk |
|
|
|
(c) |
|
|
|
||||||
|
|
(e) |
|
|
|
|
|||
Tk |
|
|
Tk |
|
|
|
|
|
|
|
|
|
= [Φ(в) Φ(e) ]; |
|
|
|
|
|
|
(в) |
|
|
||||||||||||
|
|
ΦT |
|
Φ |
= |
ΦFk ; |
|
|
||||||||||||||||
|
|
ik |
|
|
|
ik |
|
ik |
|
|
|
Fk |
Φ(e) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fk |
|
|
||
|
|
|
|
|
|
T0 |
|
|
+ |
|
|
T0 |
|
|
|
T0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
l |
|
|
(в) |
|
|
T |
(c) |
|
|
T |
(c) |
|
|
|||||||
|
|
P = |
|
k |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
k |
|
T |
|
|
|
k |
|
T |
|
|
k |
T |
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
k |
|
6T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
+ |
|
0 |
|
|
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
(c) |
|
|
|
(c) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(e) |
|
|||||||
|
|
|
|
|
|
|
|
Tk |
|
|
|
|
|
Tk |
|
|
|
Tk |
|
|
||||
В |
случае, |
когда Tk(s) = const = Тk, |
т.е. когда T(в) = |
T(с) = |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
k |
= T(е) |
, при Т0 = Tk матрица Рk примет вид: |
|
|
|
|
|
||||||||||||||||||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pk |
= |
|
l |
k |
|
2 |
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
6Tk |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|||||
Наконец, |
при |
|
Фik(s) = |
|
|
const |
= Фik, |
ФFk(s) = const = ФFk, |
||||||||||||||||
Tk = const определённый интеграл соотношения |
(13.3) вычисляет- |
|||||||||||||
ся наиболее просто. |
|
|
|
|
|
|
|
|
|
|
||||
|
Φ |
ik |
Φ |
Fk |
lk |
|
l |
k |
|
|
= ΦT P Φ |
|
|
|
|
|
|
∫ds = Φ |
ik |
|
Φ |
Fk |
Fk |
, |
(13.7) |
||||
|
|
|
|
|
|
|
||||||||
|
|
Tk |
|
0 |
Tk |
ik k |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
где Pk = Tlk .
k
В этой ситуации для k-го участка все матрицы формулы (13.7) формируются из одного элемента.
9 |
10 |

13.4. Определение перемещений от силового воздействия
В одиннадцатой лекции (п. 11.3) упоминалось, что влияние деформаций изгиба, сдвига и растяжения–сжатия на величины перемещений в сооружениях неодинаково. В рамах и балках преимущественное влияние на величины перемещений оказывают деформации изгиба, в комбинированных системах, – как деформации изгиба, так и растяжения–сжатия, в фермах при узловой передаче нагрузки – только деформации растяжения–сжатия. В ряде случаев, например, при расчёте арок и пространственных стержневых систем определение перемещений производится с учётом всех видов деформаций. С учётом данного обстоятельства рассмотрим определение перемещений в сооружениях различного типа от силового воздействия в матричной форме.
1 . БАЛКИ И РАМЫ . Приняв в соотношении (13.2)
Фik(s) = Mik(s), ФFk(s) = MFk(s), Tk(s) = EJk(s), Pk = BMk, перепишем формулу Мора дляопределения перемещений вматричнойформе:
nM lk Mik (s)MFk (s)ds |
nM |
T |
T |
BM MF . (13.8) |
|
F = ∑ ∫ |
EJk (s) |
= ∑M ik |
BMk MFk = M i |
||
k=1 0 |
k=1 |
|
|
|
|
В выражении (13.8): nM – количество грузовых участков для изгибающих моментов; Mi – матрица изгибающих моментов от единичных факторов, приложенных в направлении определяемых перемещений, или матрица изгибающих моментов в единичных состояниях заданного сооружения; ВМ – матрица внутренней упругой податливости сооружения, учитывающая деформации изгиба его элементов; MF – матрица изгибающих моментов от силового воздействия.
Матрицы Mi, ВМ, MF являются блочными, причём количество блоков в них равно числу грузовых участков для изгибающих моментов (n = nM).
|
Mi1 |
|
|
||
|
|
|
|
|
|
|
Mi2 |
|
|
||
M |
= |
M |
, B |
|
|
i |
Mik |
|
M |
||
|
|
M |
|
|
|
|
|
|
|
|
|
|
M |
in |
|
|
|
|
|
|
|
|
|
BM1 |
|
O |
|
|
M |
F1 |
|
|
|
BM2 |
|
|
|
|
|
||
|
|
|
MF2 |
|
||||
|
O |
|
|
|
|
M |
|
|
= |
|
BMk |
, M |
F |
= |
|
|
. (13.9) |
|
O |
|
MFk |
|
||||
|
O |
|
|
|
M |
|
||
|
|
|
|
|
||||
|
|
|
|
|
M |
Fn |
|
|
|
|
|
BMn |
|
|
|
|
|
Структура блоков, входящих в матрицы (13.9) для любого грузового участка, определяется видом функций, входящих в подынтегральное выражение соотношения (13.8).
В общем случае, когда на k-ом грузовом участке с переменной изгибной жёсткостью поперечного сечения EJk(s) есть распределённая нагрузка, функция MFk(s) нелинейна. Тогда в соответствии с выражением (13.2) имеем:
|
|
|
M(в) |
= [Mik(в) |
|
|
|
Mik(e) ]; MFk |
M(в) |
|
||||||||||||||
Mik |
|
|
|
ik |
|
Mik(c) |
|
|
Fk |
|
|
|||||||||||||
= |
Mik(c) ; MikT |
= M |
(c)Fk |
; |
|
|||||||||||||||||||
|
|
|
|
M |
(e) |
|
|
|
|
|
|
|
|
|
|
M |
(e) |
|
|
|||||
|
|
|
|
ik |
|
|
|
|
|
|
|
|
|
|
|
Fk |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(в) |
|
|
|
|
|
(13.10) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
EJ(в) |
|
|
|
|
|
|
|
|
0 |
|
0 |
|
||||||
|
|
|
|
lk |
|
k |
4 |
|
|
|
|
|
lk |
βk |
|
|
||||||||
B |
|
= |
|
0 |
|
|
|
|
0 |
|
= |
|
0 |
4β(c) |
|
0 |
. |
|||||||
Mk |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
6 |
|
|
|
EJ(c)k |
|
|
|
6EJ0 |
|
k |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
0 |
0 |
β |
(e) |
|
||||||||||
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
1 |
|
|
|
|
k |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
EJ(e) |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь в, с, е – обозначения сечений соответственно в начале, |
|||||||||||||||||||||||
середине и в конце k-го участка; EJ0 – произвольное число; β(в) , |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
β(c) , β(e) |
– относительные изгибные податливости сечений в, с, е |
||||||||||
k |
k |
|
= EJ0 |
|
β(c) = EJ0 |
|
β(e) = EJ0 . |
||||
|
|
β(в) |
; |
; |
|||||||
|
|
k |
|
EJ(в) |
|
k |
EJ(c) |
|
k |
EJ(e) |
|
|
|
|
|
k |
|
|
k |
|
|
k |
|
11 |
12 |

Если EJk(s) = const = EJk, то приняв EJ0 |
= EJ(в) |
= EJ(c) |
= |
|||
|
|
|
|
k |
k |
|
EJ(e) |
= EJk, получим β(в) = β(c) = β(e) = 1 и тогда матрица (13.10) |
|||||
k |
k |
k |
k |
|
|
|
внутренней упругой податливости для k-го грузового участка преобразуется следующим образом:
1 0 0
BMk = lk 0 4 0 . (13.11) 6EJk 0 0 1
При отсутствии на грузовом участке распределённой нагрузки функция MFk(s) будет линейной. Функция Mik(s) при определении перемещений отдельных сечений и узлов стержневых систем также линейна. В этой ситуации, учитывая соотношение
(13.6), получим:
|
|
(в) |
|
= [M(в) M(e) ]; M |
|
(в) |
M |
ik |
= M ik ; MT |
Fk |
= M Fk ; |
||
|
(e) |
ik |
ik ik |
(e) |
||
|
|
M ik |
|
|
|
M Fk |
|
|
|
|
|
|
|
|
|
|
|
EJ |
0 |
+ |
|
EJ |
0 |
|
|
|
|
EJ |
0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
lk |
|
|
|
|
|
|
|
EJ(c)k |
|
|
|
|
EJ(c)k |
|
|
||||||||||||||
B |
|
= |
|
|
|
|
EJ(kв) |
|
|
|
|
|
|
|
|
= |
||||||||||||||||||
Mk |
|
6EJ |
0 |
|
|
|
|
|
|
|
EJ0 |
|
|
|
|
|
|
EJ0 |
+ |
|
EJ0 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(13.12) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
(c) |
|
|
EJ |
(c) |
|
EJ |
(e) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
k |
|
|
k |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
lk |
|
|
|
(в) |
|
|
|
(c) |
|
|
|
(c) |
|
|
|
|
|
|
||||||||||
|
|
|
= |
|
|
|
βk |
+βk |
|
|
|
βk |
|
|
. |
|
|
|
||||||||||||||||
|
|
|
|
6EJ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
β(c) |
|
|
|
β(c) +β(e) |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
k |
|
|
k |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
При EJk(s) = const = EJk и EJ0 = EJk матрица (13.12) перепи- |
||||||||||||||||||||||||||||||||||
шется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
Mk |
= |
|
|
lk |
|
|
2 1 . |
|
|
|
|
|
(13.13) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6EJk 1 2 |
|
|
|
|
|
|
||||||||
Число строк в блочных матрицах (13.9) Mi, MF, BM равно суммарному числу сечений, в которых фиксируются изгибающие моменты для вычисления требуемой матрицы перемещений. В матрице Mi число столбцов равно числу определяемых переме-
щений, в матрице MF – числу внешних воздействий на сооружение, в матрице BM – числу строк.
2 . ФЕ Р М Ы . В фермах при узловой передаче нагрузки усилия в сечениях стержней постоянны. Довольно часто и жёсткости поперечных сечений стержней на растяжение–сжатие также постоянны. В этом случае при Фik = Nik = const, ФFk = NFk
= const, Tk = EAk = const соотношение (13.7) для k-го стержня примет вид:
|
|
|
|
|
Nik NFk |
l |
Nik lk NFk |
|
|
|
|
|
|
|
∫kds = |
= NT BNk NFk , |
|||
|
|
|
|
|
|
EAk |
|||
|
|
|
|
|
EAk 0 |
ik |
|||
|
|
|
|
|
|
|
|
|
|
где |
B |
Nk |
= |
lk |
[1]. |
|
|
||
EAk |
|
|
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Распространяя последнее соотношение на всю форму, имеющую n стержней, получим:
n |
Nik lk NFk |
|
T |
|
|
|
F = ∑ |
|
= N |
|
BN NF . |
(13.14) |
|
EAk |
i |
|||||
k=1 |
|
|
|
|||
|
|
|
|
|
В формуле (13.14): Ni – матрица продольных усилий в стержнях фермы от единичных факторов, приложенных в направлении определяемых перемещений; NF – матрица продольных усилий в стержнях фермы от заданного силового воздействия; BN – матрица внутренней упругой податливости фермы, учитывающая деформации растяжения–сжатия её стержней, т.е.
|
l1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
EA1 |
|
|
O |
|
|
|||||
|
|
|
l2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
EA2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
O |
|
|
|
|
|
(13.15) |
BN = |
|
|
|
|
l |
k |
|
. |
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
EAk |
|
|||||
|
|
|
O |
|
|
|||||
|
|
|
|
|
O |
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EAn |
|
|
13 |
14 |

Число строк матриц Ni, NF и BN равно числу стержней фермы. В матрице Ni число столбцов равно числу искомых перемещений, в матрице NF – числу внешних комбинаций узловых нагрузок, в диагональной матрице BN – числу строк.
3 . КОМБИНИРОВАННЫЕ СИСТЕМЫ . В комбиниро-
ванных системах, в которых, как правило, при определении перемещений пренебрегают деформациями сдвига, формула Мора имеет вид:
|
nMlk M |
ik |
(s)M |
Fk |
(s)ds |
nN lk N |
ik |
(s)N |
Fk |
(s)ds |
|
||
jF |
= ∑ ∫ |
|
|
|
+ ∑ ∫ |
|
|
|
. |
||||
|
|
EJk (s) |
|
|
|
EAk (s) |
|||||||
|
k=1 0 |
|
|
k=1 0 |
|
|
|||||||
Последнее выражение в этой формуле предусматривает учёт деформаций растяжения–сжатия в незагруженных элементах, имеющих по концам цилиндрические шарниры и преимущественно постоянную жёсткость поперечного сечения на растяже- ние–сжатие. Таким образом, эти элементы комбинированных систем работают как стержни ферм при узловой передаче нагрузки. С учётом этого обстоятельства формулу Мора для комбинированных систем можно представить так:
|
nMlk Mik (s)MFk (s)ds |
nN |
Nik NFklk |
T |
|
||
F |
= ∑ ∫ |
|
+ ∑ |
|
|
= L BLF |
. (13.16) |
EJk (s) |
|
EAk |
|||||
|
k=1 0 |
k=1 |
i |
|
|||
|
|
|
|
|
|
|
|
Здесь nN – число стержней, в которых необходимо учесть деформации растяжения–сжатия; Li – матрица внутренних усилий (изгибающих моментов и продольных сил) от единичных факторов, приложенных в направлении определяемых перемещений; LF – матрица внутренних усилий от внешних силовых воздействий; В – матрица упругой внутренней податливости комбинированной системы, учитывающей как деформации изгиба, так и деформации растяжения–сжатия. Упомянутые матрицы имеют блочную структуру:
L |
|
M |
|
M |
|
B |
M |
0 |
(13.17) |
|
i |
= i ; L |
F |
= |
F ; |
B = |
|
. |
|||
|
Ni |
NF |
|
0 BN |
|
|||||
Формирование блоков матриц (13.17) производится: Mi, MF, BM – по правилам, изложенным выше для рам и балок; Ni, NF, BN
– по соответствующим правилам для ферм.
4 . ПЛОСКИЕ СТЕРЖНЕВЫЕ СИСТЕМЫ . Для этих
систем с учётом влияния всех видов деформаций на перемещения формулаМора вматричной форме запишется следующим образом:
l |
|
Mik (s)MFk (s)ds |
|
|
n |
l |
|
|
Qik (s)MFk (s)ds |
|
||||||||
F = n∑M ∫k |
+ ∑Q |
∫k k τk |
|
+ |
||||||||||||||
k=1 0 |
|
EJk (s) |
|
|
|
k=1 0 |
|
|
|
GAk (s) |
(13.18) |
|||||||
|
|
nN lk N |
|
(s)M |
|
(s)ds |
|
|
|
|
||||||||
|
|
ik |
Fk |
|
|
T |
|
|
|
|||||||||
|
|
+ ∑ |
∫ |
|
|
|
|
|
|
|
|
|
= Li |
BLF . |
|
|
||
|
|
|
|
EAk (s) |
|
|
|
|||||||||||
|
|
k=1 0 |
|
|
|
|
|
|
|
|
|
|||||||
В соотношении (13.18): |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Mi |
|
|
|
|
MF |
|
|
|
BM 0 0 |
|
||||||
Li |
|
|
|
|
|
= |
|
|
|
|
|
|
|
0 BQ 0 |
|
|||
= Qi |
; LF |
QF |
; B = |
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Ni |
|
|
|
|
NF |
|
|
|
|
0 0 BN |
||||||
В матрице В блок ВQ учитывает деформации сдвига элементов сооружения.
Порядок формирования блоков Mi, Ni, MF, NF, BM и BN изложен выше. Вид блоков Qi, QF, BQ зависит от характеристик грузовых участков для поперечных сил: есть ли распределённая нагрузка на этих участках, каков закон изменения жёсткости поперечного сечения на сдвиг GAk(s)? В частности, при GAk(s) = = const = GAk и равномерно распределённой нагрузки для k-го грузового участка имеем:
|
|
Q(в) |
|
|
Q(в) |
|
|
l |
k |
k |
τk |
2 1 |
|
|||
Q |
ik |
= |
ik ; Q |
Fk |
= |
|
Fk ; B |
Qk |
= |
|
|
. |
|
|||
|
|
|
|
|
||||||||||||
|
Q(e) |
|
Q(e) |
|
GA |
k |
1 2 |
|
||||||||
|
|
|
ik |
|
|
|
Fk |
|
|
|
|
|
|
|
|
|
Если распределённая нагрузка на рассматриваемом грузовом |
||||||||||||||||
участке отсутствует, то |
Q(в) |
= Q(e) = Q |
, Q(в) |
= Q(e) = Q |
, и |
|||||||||||
|
|
|
|
|
ik |
|
ik |
ik |
|
|
|
Fik |
Fk |
Fk |
||
при GAk(s) = const = GAk матрицы Qik, QFk, BQk будут состоять из одного элемента, причём
B |
Qk |
= |
lk kτk |
[1] . |
|
GAk |
|||||
|
|
|
|||
|
|
|
|
15 |
16 |

5 . ПР О С Т Р А Н С Т В Е Н Н Ы Е СТЕРЖНЕВЫЕ СИСТЕ -
МЫ . В общей формуле Мора, записанной в матричной форме для определения перемещений в этих системах
F = LTi BLF ,
элементами матриц Li и LF являются изгибающие моменты и поперечные силы, действующие в главных плоскостях инерции поперечных сечений, продольные силы и крутящие моменты. Матрица внутренней податливости сооружения В в этом случае включает в себя блоки, учитывающие все виды деформаций (изгиба и сдвига в двух взаимно перпендикулярных плоскостях, рас- тяжения–сжатия и кручения).
ПРИМЕР 13.4.1. В трёхшарнирной раме, показанной на рис. 13.4,а, изгибная жёсткость поперечного сечения ригеля задана и равна EJ, стоек – 0,5EJ. Требуется определить горизонтальное перемещение и поворот узла К отдельно от равномерно распределённой нагрузки q = 2 кН/м и от сосредоточенного момента М = 12 кН м, т.е. требуется вычислить элементы матрицы перемещений
|
|
(q) |
(M) |
|
F |
= |
kx |
kx |
. |
θ(q) |
θ(M) |
|||
|
|
k |
k |
|
Искомую матрицу перемещений определим по формуле
(13.8)
F= MiT BM MF .
1.Построение эпюр изгибающих моментов Mq и MМ отдель-
но от равномерно распределённой нагрузки и от сосредоточенного момента (рис. 13.4,б).
2.Построение эпюр изгибающих моментов M1 и M2 от единичных силовых факторов F = 1 и М = 1, приложенных в направлении определяемых перемещений (рис. 13.4,в).
3.Нумерация грузовых участков для изгибающих моментов
исечений, в которых изгибающие моменты будем фиксировать
17 |
18 |
