Контрольная работа №2

Задачи №69, 79, 89, 99, 109, 119, 129

Дифференциальное и интегральное исчисление. Функции

нескольких переменных.

Задача 1(69).

Найти производные следующих функций:

а) ; б) ; в) .

Решение:

а) .

Находим:

.

б)

Находим:

в) .

Переменная  называется параметром и может принимать значения от «минус бесконечности» до «плюс бесконечности».

Для нахождения производной параметрической функции существует формула: .

.

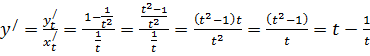Ответ: а), б) , в) .

Задача 2(79).

Вычислить приближенно , заменяя приращение функции ее дифференциалом: .

Решение: Формула для приближенного вычисления с помощью дифференциала: .

На первом этапе необходимо составить функцию . По условию предложено вычислить кубический корень из числа: , поэтому соответствующая функция имеет вид: . Нам нужно с помощью формулы найти приближенное значение .

Смотрим на левую часть формулы , число 650 необходимо представить в виде . Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе:  – получилось чуть больше 5, это важный ориентир для решения.

В качестве  подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение   должно быть как можно ближе к 625. В данном случае: . Действительно: .

Если , то приращение аргумента: .

Итак, число 650 представлено в виде суммы .

Далее работаем с правой частью формулы .

Сначала вычислим значение функции в точке . Собственно, это уже сделано ранее: . Дифференциал в точке находится по формуле: .  Из формулы следует, что нужно взять первую производную:

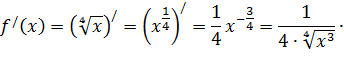И найти её значение в точке :

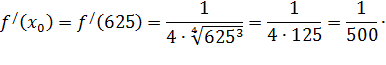Таким образом:

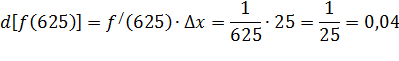Согласно формуле : .

Найденное приближенное значение достаточно близко к значению   , вычисленному с помощью микрокалькулятора.

Ответ: .

Задача 3(89).

Заданные функции исследовать методами дифференциального исчисления. На основании результатов исследований построить графики функций:

А) ; Б) .

Решение:

А)

 1. Область определения функции: .

2. Пересечение с осью абсцисс (OX): .

Пересечение с осью ординат (OY): .

3. Поведение функции на бесконечности:

,

.

4. Исследование функции на чётность/нечётность: функция не является ни четной, ни нечетной.

5. Производная функции равна:

.

Нули производной: ,

,

.

				2
	+	0	-	0	+
		Точка максимума		Точка минимума

6. Находим вторую производную:

,

,

,

.

	-	0	+
		Точка перегиба

7. Асимптоты:

Вертикальных и горизонтальных асимптот нет.

Попробуем найти наклонные асимптоты: , где ,

.

.

Следовательно, наклонных асимптот нет.

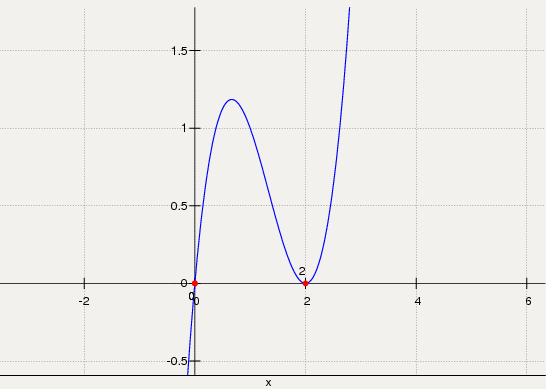
8. Строим график функции:

Б) .

 1. Область определения функции: .

2. Пересечение с осью абсцисс (OX): .

3. Поведение функции на бесконечности и области определения функции:

, .

, .

4. Исследование функции на чётность-нечётность: функция не является ни четной, ни нечетной.

5. Производная функции равна:

.

Нули производной: ,

.

.

	-	Не сущ.	-	0	+
				Точка минимума

6. Находим вторую производную:

,

,

.

.

				0
	+	0	-	Не сущ.	+
		Точка перегиба

7. Асимптоты:

Вертикальные асимптоты: .

Попробуем найти наклонные асимптоты: , где

,

.

.

Наклонных асимптот нет.

8. Строим график функции:

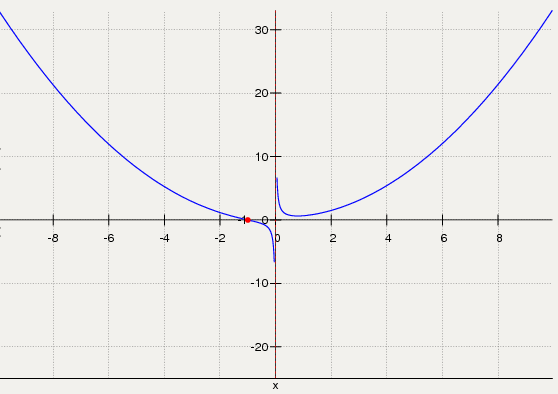
Задача 4(99). Найти интегралы. Результаты проверить дифференцированием.

а) ; б) ; в) ; г) .

Решение:

а)

.

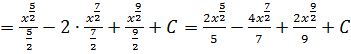Проверка:

.

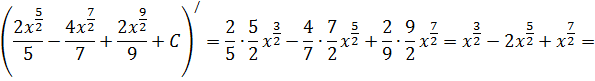
б)

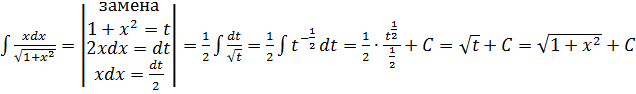
Проверка:

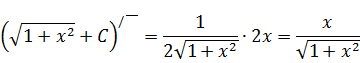
в)

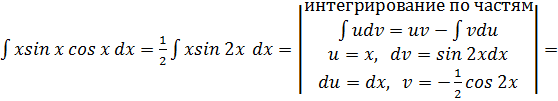
Проверка:

.

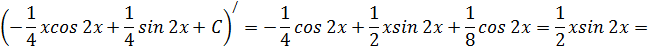
г)

.

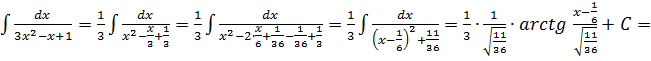
Проверка:

.

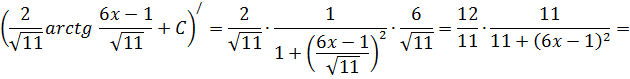
Ответ: а) ; б) ;

в) ; г) .

Задача 5(109).

Н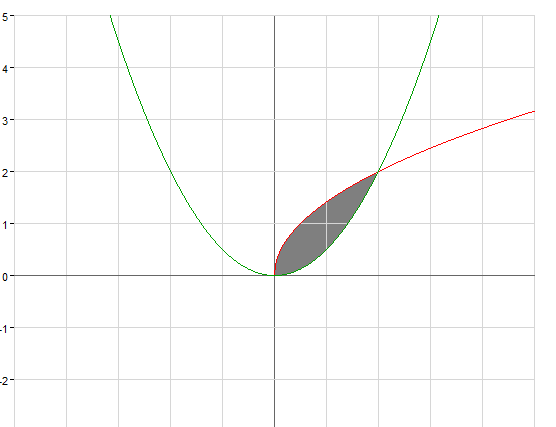айти площадь фигуры, ограниченной заданными линиями. Сделать рисунок.

.

Решение:

Если на отрезке [a; b] некоторая непрерывная функция  больше либо равна некоторой непрерывной функции , то площадь соответствующей фигуры можно найти по формуле:  .

Найдем точки пересечения данных функций:

;

;

.

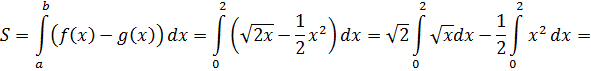
(кв.ед.)

Ответ: (кв.ед.)

Задача 6(119).

Вычислить несобственный интеграл или доказать его расходимость: .

Решение:

Если существует конечный предел , то этот предел называетсянесобственным интегралом от функции f(x) на интервале [a, ).

Обозначение:

Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.

Если предел не существует или бесконечен, то несобственный интеграл расходится.

По определению:

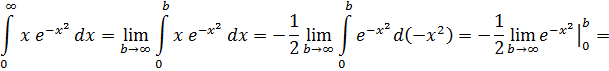
Несобственный интеграл сходиться.

Ответ: сходиться.

Задача 7(129).

Задана функция . Найти:

а) наименьшее и наибольшее значение функции в ограниченной области D,

б) вектор - градиент функции в точке А. Область D и вектор изобразить на чертеже.

а) D:; б) .

Решение: а) наименьшее и наибольшее значение функции в ограниченной области D:

Точки, в которыхфункция принимает наибольшее и наименьшее значения, могут находиться как внутри области, так и на её границе. Если функция принимает наибольшее (наименьшее) значение во внутренней точке области, то в этой точке частные производные

, равны нулю (как и в очке экстремума). Решив систему уравнений найдем одну стационарную точку Р (0;0), в которых обе частные производные равны нулю. Она не принадлежит области D, следовательно, мы её не будем учитывать при дальнейших вычислениях.

Исследуем значения функции на границе области D. На стороне AВ

треугольника АBC функция имеет вид . Находим стационарные точки , получаем . Таким образом, точка (-1; 0) не принадлежит области D. На стороне АC треугольника АBC функция имеет вид . Находим стационарные точки , получаем . Таким образом, точка Q(; ) принадлежит области D, лежит на границе области. Значение функции в этой точке . Находим наибольшее и наименьшее значения на стороне ВC: . Здесь , , тогда

, т.е. точка (1; 1) не принадлежит области D.

Найдем значения, функции в точках A (-1, 1), В(-1, 3), C(0, 2):