
Вариант №9
Контрольная работа №1
Задачи №9, 19, 29, 39, 49, 59
Линейная и векторная алгебра. Аналитическая геометрия.
Введение в математический анализ.
Задача 1(9).
Применяя метод Гаусса исключения неизвестных, решить систему линейных уравнений. Сделать проверку найденного решения.
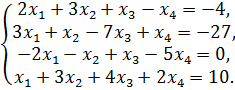
Решение:
Немного теории:
Метод Гаусса.
Метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Рассмотрим
систему линейных уравнений:
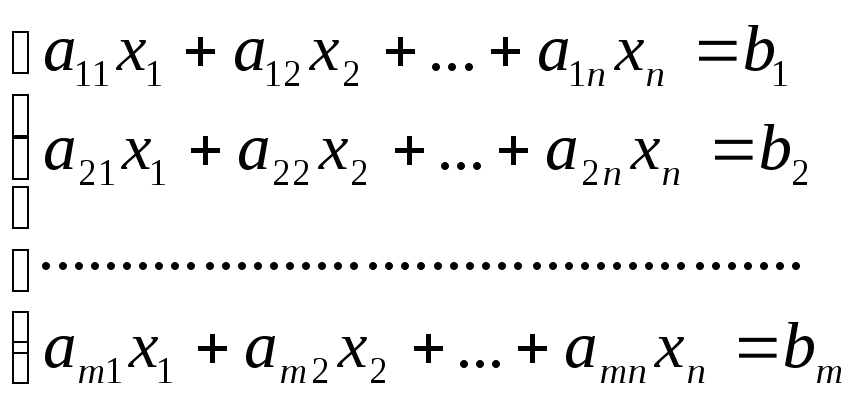
Разделим обе части 1–го уравнения на a11 0, затем:
1) умножим на а21 и вычтем из второго уравнения
2) умножим на а31 и вычтем из третьего уравнения
и т.д.
Получим:
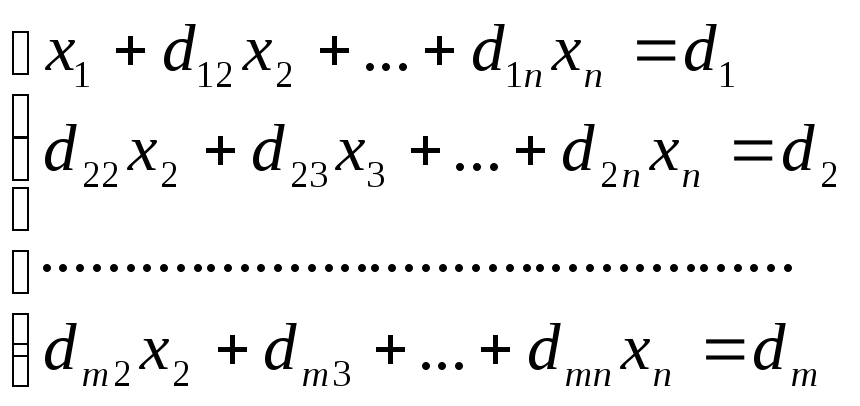 ,
где d1j
= a1j/a11,
j
= 2, 3, …, n+1.
,
где d1j
= a1j/a11,
j
= 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
Применительно к нашей задаче:
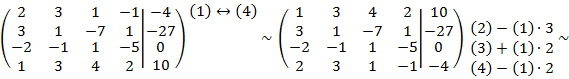


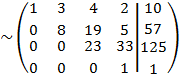
Следовательно, система примет вид:
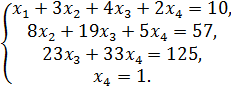
Отсюда находим все оставшиеся неизвестные:
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Заданная система уравнений имеет единственное решение:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
ПРОВЕРКА:
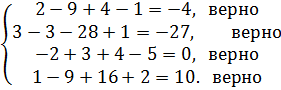
Ответ:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Задача 2(19).
Даны
векторы![]() (-2;
-1; 1),
(-2;
-1; 1),![]() (2;
3; 0),
(2;
3; 0),![]() (-4;
2; 3) и
(-4;
2; 3) и
![]() (-10;
-9; 3) в некотором базисе. Показать, что
векторы
(-10;
-9; 3) в некотором базисе. Показать, что
векторы
![]() ,
,![]() и
и![]() образуют
базис и найти координаты вектора
образуют
базис и найти координаты вектора
![]() в этом базисе. Систему линейных уравнений
решить методом Крамера.
в этом базисе. Систему линейных уравнений
решить методом Крамера.
Решение:
Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:
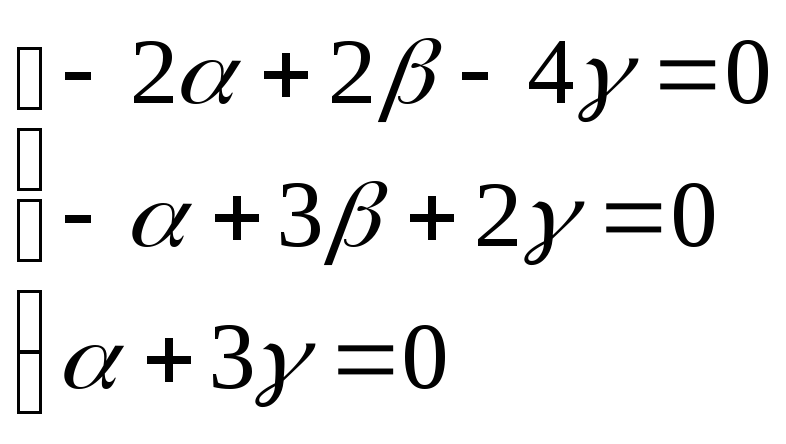 линейно
независимы.
линейно
независимы.
Тогда
![]() .
.
Это условие выполняется, если определитель матрицы системы отличен от нуля.
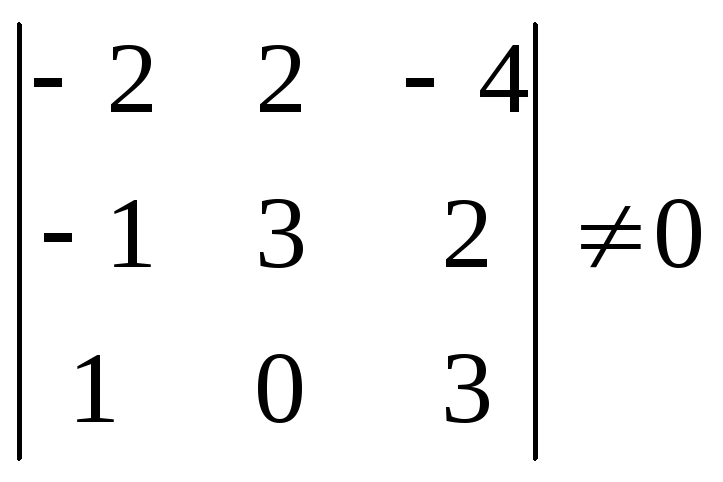

 0
0
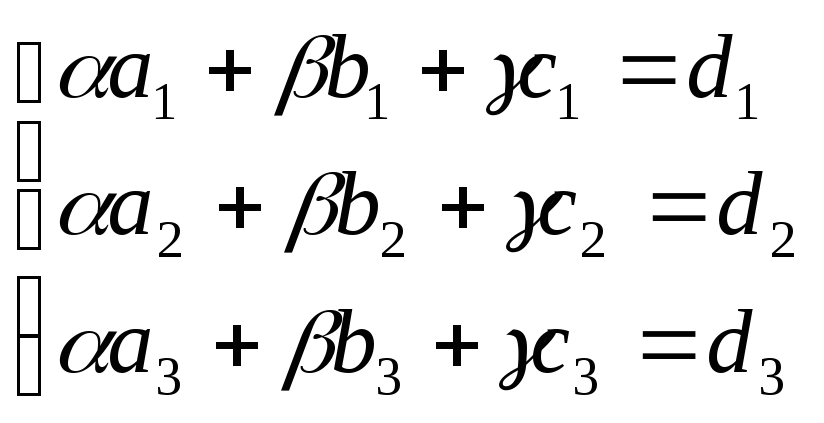 Для
решения этой системы воспользуемся
методом Крамера.
Для
решения этой системы воспользуемся
методом Крамера.
1
=
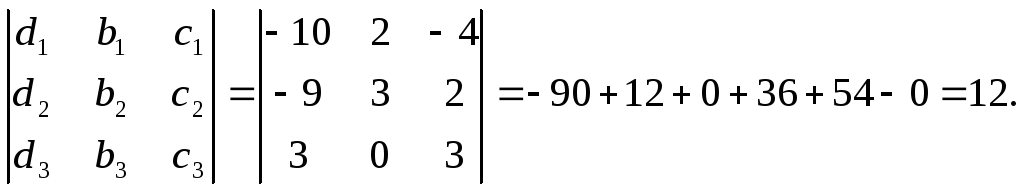
![]() ;
;
2
=
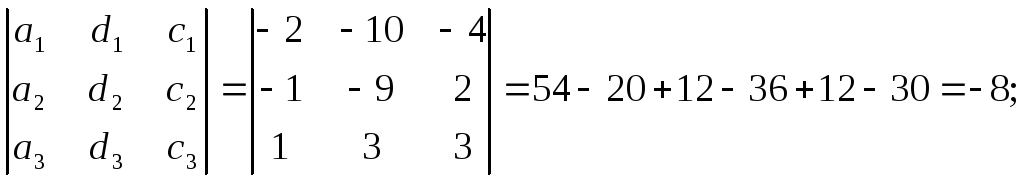
![]()
3
=
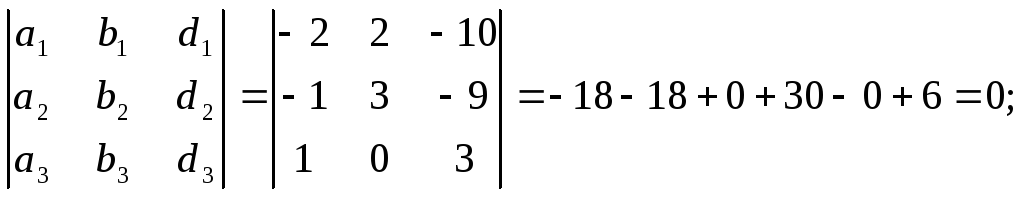
![]()
Итого,
координаты вектора
![]() в
базисе
в
базисе
![]() ,
,![]() ,
,![]() :
:
![]() { 3, -2, 0}.
{ 3, -2, 0}.
Ответ:
![]() { 3, -2, 0}
{ 3, -2, 0}
Задача 3(29).
Даны
вершины ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
пирамиды.
,
пирамиды.
Найти:
длину ребра
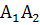 ;
;угол между ребрами
 и
и 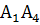 ;
;уравнение грани
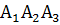 и ее площадь;
и ее площадь;уравнение высоты, опущенной из вершины
 на грань
на грань 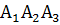 .
.
Решение:
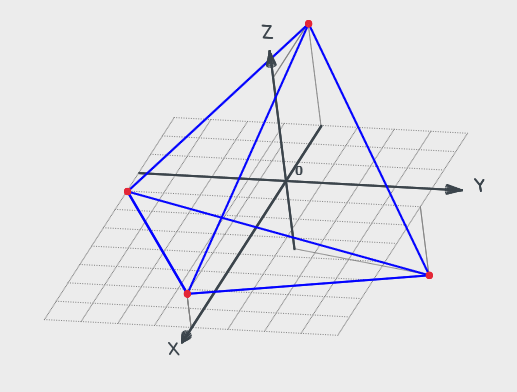
Найти длину ребра А1А2.
Чтобы
найти компоненты вектора нужно из
координат его конца вычесть координаты
начала. Если заданы точки А(x1,
y1,
z1),
B(x2,
y2,
z2),
то
![]() =
(x2
–
x1,
y2
– y1,
z2
– z1).
=
(x2
–
x1,
y2
– y1,
z2
– z1).
Длина
вектора в координатах
определяется как расстояние между
точками начала и конца вектора. Если
заданы две точки в пространстве А(х1,
y1,
z1),
B(x2,
y2,
z2),
то
![]() .
.
В
нашем случае:
![]()
Найти угол между ребрами А1А2 и А1А4.
Скалярным
произведением векторов
![]() и
и![]() называется число, равное произведению
длин этих сторон на косинус угла между
ними:
называется число, равное произведению
длин этих сторон на косинус угла между
ними:![]()
![]() =
=![]()
![]() cos.
cos.
Если
рассматривать векторы
![]() в
декартовой прямоугольной системе
координат, то
в
декартовой прямоугольной системе
координат, то![]()
![]() =xa
xb
+ ya
yb
+ za
zb.
=xa
xb
+ ya
yb
+ za
zb.
Используя
полученные равенства, получаем формулу
для вычисления угла между векторами:
![]() .
.
Находим:
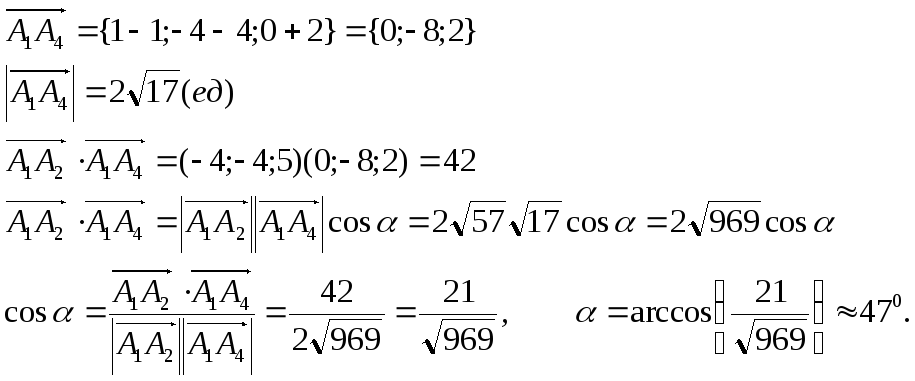
Найти уравнение грани
 и ее площадь.
и ее площадь.
Воспользуемся формулой уравнения плоскости, проходящей через три точки.
Уравнение
плоскости, проходящей через три точки:
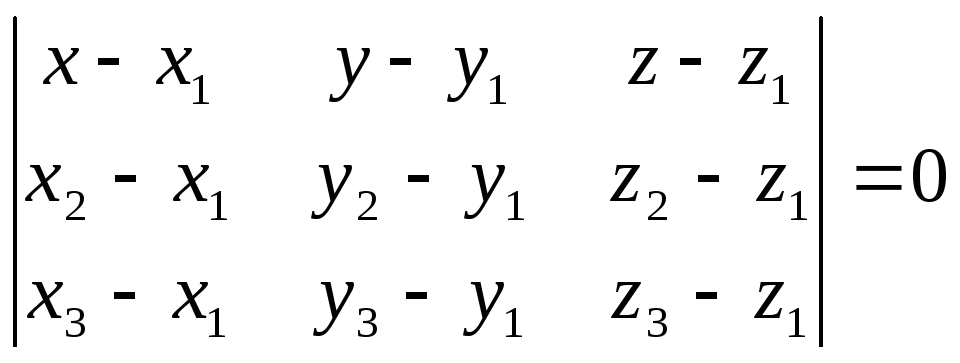
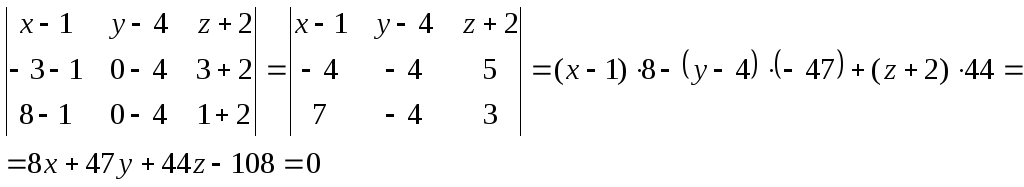
![]() ,
,
![]() .
– уравнение грани
.
– уравнение грани ![]() .
.
Вычисляем
площадь грани грани ![]() :
:
![]() ,
,
![]() .
.
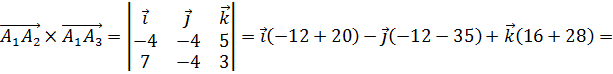
![]() .
.
![]() .
.
![]() .
.
4.
Найти уравнение высоты, опущенной из
вершины ![]() на грань
на грань ![]() .
.
Уравнение
высоты, будем искать, как уравнение
прямой, проходящей через точку ![]() перпендикулярно
плоскости
перпендикулярно
плоскости
![]() (
(![]() ):
):
![]() .
.
Так
как вектор с координатами ![]() является
нормальным вектором плоскости
является
нормальным вектором плоскости ![]() ,
а следовательно, он является направляющим
вектором перпендикуляра, опущенного
на эту плоскость.
Для
искомой высоты получим:
,
а следовательно, он является направляющим
вектором перпендикуляра, опущенного
на эту плоскость.
Для
искомой высоты получим: ![]() =
=![]() .
.
Ответ:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() – уравнение грани
– уравнение грани ![]() ,
,
![]() ;
;
4)
![]() =
=![]() .
.
Задача 4(39). Составить уравнение множества точек, для каждой из которых выполняется следующее условие: разность расстояний до точек А(0, 10) и О(0,0) равна 8.
Решение:
В
задаче говориться о некотором расстоянии
до точки A до оси ординат. Обозначим
координаты неизвестной точки как
С(x,y). В декартовой
системе координат расстояние
между точками рассчитывается по
формуле (![]() .Тогда
расстояние между точками A и C:
.Тогда
расстояние между точками A и C: ![]() .
А расстояние до оси ординат будет
.
А расстояние до оси ординат будет
![]() .
Из условия задачи также известно, что
.
Из условия задачи также известно, что ![]() .
Подставим значения длин AC,CО
.
Подставим значения длин AC,CО
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Получили
уравнение гиперболы с вершиной в точке
![]() .
.
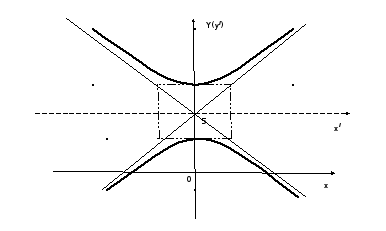
Задача 5(49).
Вычислить пределы функций:
А)
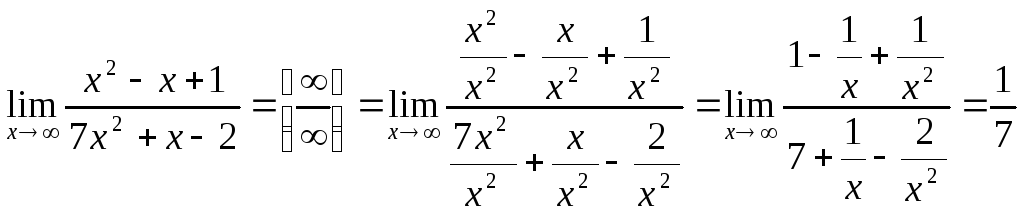 ;
;
Б)
![]() ;
;
В)
![]()
![]() .
.
Задача 6(59).
Задана
функция ![]() .
Найти все точки разрыва функции, если
они существуют. Построить график
функции.
.
Найти все точки разрыва функции, если
они существуют. Построить график
функции.
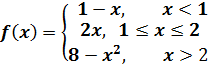
Решение:
Функция
![]() определена и непрерывна на интервалах
определена и непрерывна на интервалах
![]() ,
где она задана непрерывными элементарными
функциями. Следовательно, разрыв
возможен только в точках
,
где она задана непрерывными элементарными
функциями. Следовательно, разрыв
возможен только в точках ![]() и
и ![]() .
.
Для
точки ![]() имеем:
имеем:
![]() ,
,
![]() ,
,
![]() ,
,
т.е.
функция ![]() в точке
в точке ![]() имеет разрыв первого рода.
имеет разрыв первого рода.
Для
точки ![]() имеем:
имеем:
![]() ,
,
![]() ,
,
![]() ,
,
т
y![]() в точке
в точке ![]() непрерывна.
непрерывна.
-1
-1
1
0
1
4





2



2
x
