
Алгебра 2014
.pdf
МОСКОВСКИЙ ПЕДАГОГИЧЕСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
КАФЕДРА ТЕОРИИ И МЕТОДИКИ ОБУЧЕНИЯ МАТЕМАТИКЕ
Л.И. Боженкова
АЛГЕБРА
ТИПОВЫЕ ЗАДАНИЯ ДЛЯ ФОРМИРОВАНИЯ УУД
Москва 2014
1
УДК 372.851 |
|
ББК 74.262.21 |
Печатается по решению кафедры |
Б |
теории и методики обучения |
|
математике МПГУ |
Боженкова Л.И.
БАлгебра: Типовые задания для формирования УУД. Учебно-методическое пособие. - ФГБОУ ВПО МПГУ, Изд-во: Эйдос, 2014. – 76 с.
ISBN 978-5–902948-89-6
Содержание учебного пособия соответствует программе по алгебре и началам анализа для общеобразовательных школ, гимназий, лицеев. Учебные материалы предназначены студентам математических факультетов педагогических вузов, учителям математики для использования в процессе обучения. Материалы будут полезны ученикам в освоении школьного курса математики и для повторения, систематизации знаний.
2
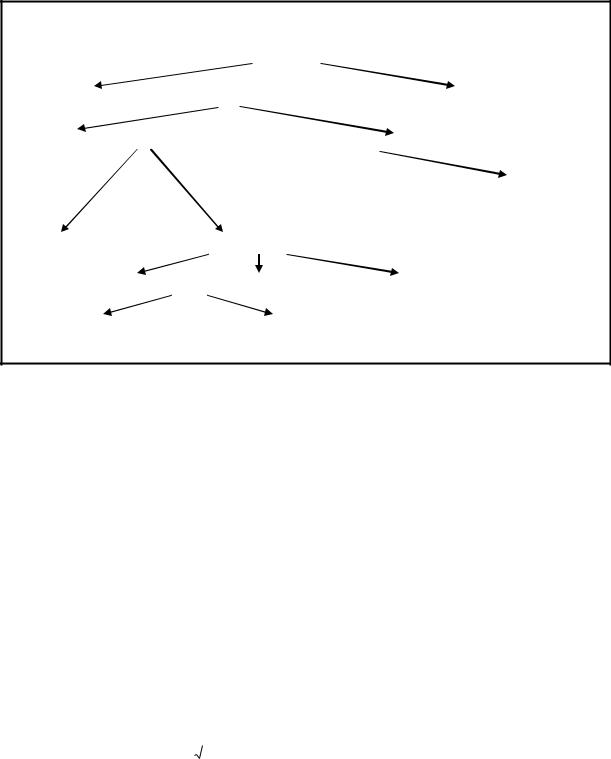
(Б) ПРИМЕРЫ ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОДУКТОВ
(по темам школьного курса алгебры)
I. ЧИСЛОВАЯ ЛИНИЯ
I.1. Классификация чисел
Комплексные числа (а + bi)
действительные числа (R) |
мнимые числа (bi) |
|
рациональные числа (Q) |
иррациональные числа |
|
|
|
трансцендентные числа (π, е, αβ, где α |
|
|
алгебраическое число, не равное 0 и 1, |
|
|
β – иррациональное) |
дробные числа |
целые числа (Z) |
|
натуральные числа (N) 0 (нуль) противоположные натуральным |
||
нечётные числа (2k – 1, k N) |
чётные числа (2k, k N) |
|
I.2. Виды математических выражений
|
Название |
Символь- |
К о м п о н е н т ы |
Название |
||||||
№ |
вида |
ная запись |
|
|
|
действия |
||||
|
выражения |
|
|
|
|
|
а |
|
b |
|
|
с - результат |
|
|
|
|
|
|
|
|
|
1. |
cумма |
a + b = c |
слагаемые |
сложение |
||||||
2. |
произведение |
a b = c |
множители |
умножение |
||||||
3. |
разность |
a |
- b = c |
уменьшае- |
вычитаемое |
вычитание |
||||
|
|
|
|
|
|
|
мое |
|
|
|
4. |
частное (от- |
a |
: b = c |
делимое |
делитель |
деление |
||||
|
ношение чи- |
|
|
|
|
|
|
|
|
|
|
сел) |
|
|
|
|
|
|
|
|
|
4а |
дробь (отно- |
|
a |
числитель |
знаменатель |
деление |
||||
|
|
|
|
|
c |
|
|
|
|
|
|
шение чисел) |
|
b |
|
|
|
|
|||
5. |
степень |
|
ab = c |
основание |
показатель |
возведение |
||||
|
|
|
|
|
|
|
степени |
степени |
в степень |
|
6. |
корень степени |
|
b |
|
c |
подкоренное |
показатель |
извлечение |
||
|
a |
|||||||||
|
b из числа а |
|
|
|
|
|
выражение |
корня |
корня |
|
7. |
логарифм |
logab = c |
основание |
выражение |
логариф- |
|||||
|
|
|
|
|
|
|
логарифма |
под знаком |
мирование |
|
|
|
|
|
|
|
|
|
логарифма |
|
|
I.3. Предписания для выполнения действий с натуральными числами
3
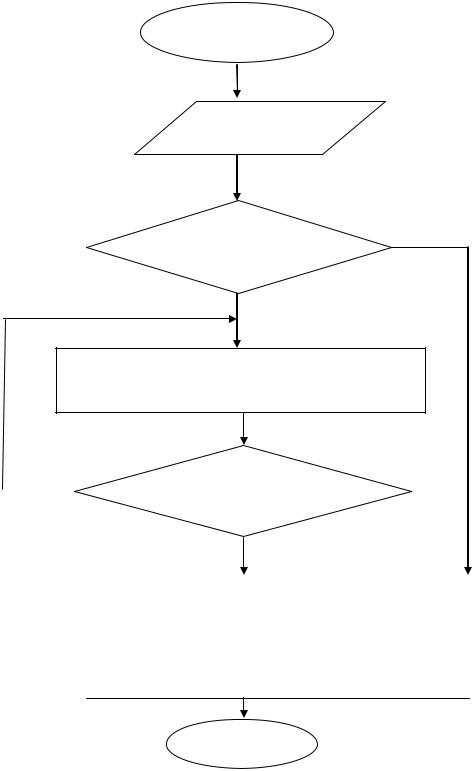
а) Предписание для сравнения натуральных чисел
НАЧАЛО
Два различных натуральных числа
числа имеют различное да количество цифр?
нет
сравнить числа поразрядно, начиная со старшего разряда (по порядку)
|
да |
цифры |
|
|
||||
|
|
|
|
|
|
|||
|
|
|
|
в одноимённых разрядах |
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
одинаковы? |
|
|
||
|
|
|
|
нет |
|
|
||
|
|
|
|
|
|
|
||
|
то число больше, у которого цифра |
|
|
то число больше, в записи |
||||
|
в одноимённом разряде обозначает |
|
|
которого больше цифр |
||||
|
большее число |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КОНЕЦ
б) Предписание для округления натуральных чисел
4

НАЧАЛО
Натуральное
число
отметить данный разряд (до которого округляют)
все цифры младших (следующих) разрядов заменить нулями
|
да |
|
цифра, |
|
нет |
||||||
|
следующая за данным разрядом |
||||||||||
|
|
|
|
|
|
|
|||||
|
|
|
от 0 до 4? |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
записать результат |
|
|
|
увеличить число, соответству- |
||||||
округления, не меняя |
|
|
|
ющее этой цифре, на 1 и запи- |
|||||||
цифру данного разряда |
|
|
|
сать результат округления |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КОНЕЦ
Упражнение № 21. Составьте набор задач для открытия предписания для округления натуральных чисел. Сформулируйте вопросы для этой деятельности. Какие УУД формируются при этом?
I.4. Принципы расширения числового множества (F до множества G)
1)F G;
2)в множестве G должны быть выполнимы операции и законы, выполнимые в
F, т.е. смысл «старых» операций в новом множестве – не меняется;
3)в множестве G выполняется новая операция (не выполнимая в множестве F);
4)расширение множества F должно быть минимальным.
5
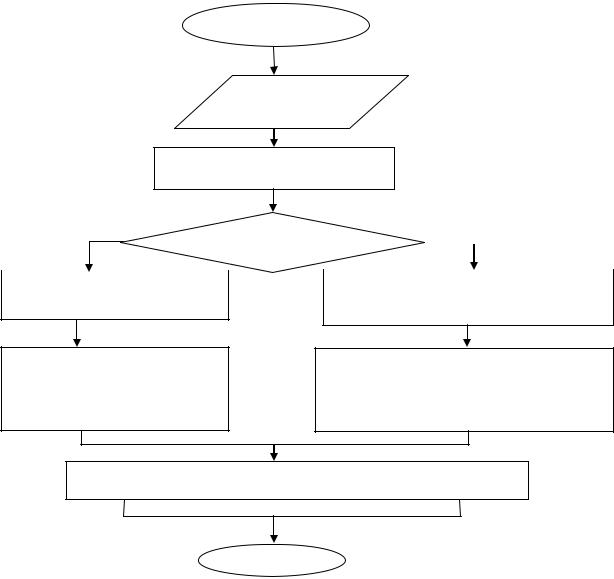
б) Предписание для сложения рациональных чисел
НАЧАЛО
Два рациональных числа, не равных 0
найти модули слагаемых
да |
Знаки чисел одинаковые? |
нет |
|||
|
|
|
|||
|
|
|
|||
сложить модули чисел |
из большего модуля числа |
||||
вычесть меньший модуль числа
записать перед полученным результатом сложения общий знак чисел
записать, перед полученным результатом вычитания модулей, знак числа, модуль которого больше
сложение данных рациональных чисел выполнено
КОНЕЦ
6
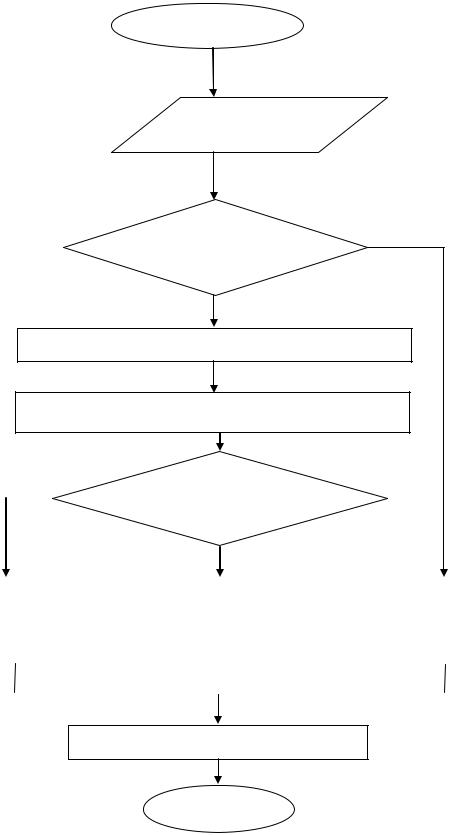
в) Предписание для умножения целых чисел
НАЧАЛО
Произведение неcкольких чисел
Хотя бы 1 из множителей да
равен 0?
нет
выполнить умножение модулей множителей
сосчитать число отрицательных множителей
|
|
да |
|
|
Число |
|
|
||
|
|
отрицательных множителей – |
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
чётно? |
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
записать перед произ- |
|
записать перед произ- |
|
произведение |
|||||
ведением модулей |
|
ведением модулей |
|
равно 0 |
|||||
знак « + » |
|
|
знак « - » |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
записать результат умножения
КОНЕЦ
Упражнение № 22. Организуйте деятельность учащихся, направленную на обобщение действия умножения целых чисел. Какие УУД при этом формируются?
7
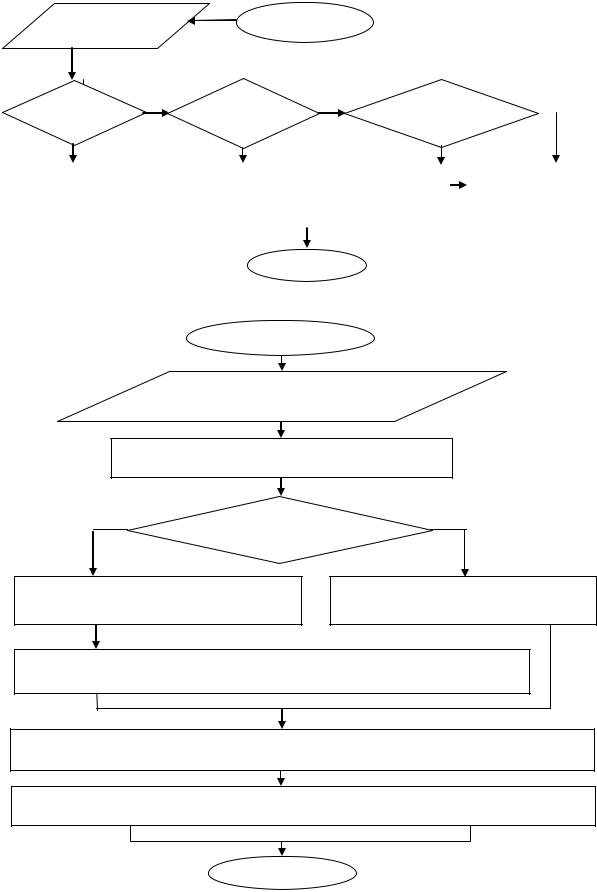
г) Предписание для деления рациональных чисел.
Два рациональ- |
НАЧАЛО |
|
|
|
|
|
|
||||
ных числа |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
делитель |
нет |
делимое |
нет |
знаки де- |
нет |
||||||
лимого и делителя |
|||||||||||
равен 0? |
|
равно 0? |
|
|
|
||||||
|
|
разные? |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
да |
|
да |
|
да |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
на нуль |
|
записать |
|
записать |
|
|
выполнить де- |
||||
делить нельзя |
|
результат: 0 |
|
знак « - » |
|
|
ление модулей |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КОНЕЦ
д) Предписание для приведения дробей к наименьшему общему знаменателю
(НОЗ)
НАЧАЛО
Сумма нескольких обыкновенных дробей с разными знаменателями
зафиксировать знаменатели дробей
нет |
знаме- |
да |
|
натели взаимно-простые |
|||
|
|
||
|
числа? |
|
разложить на простые множите-
ли знаменатель каждой дроби
найти произведение знамена-
телей дробей - НОЗ
выписать любое разложение и добавить в качестве множителей,
недостающие множители из других разложений - НОЗ
для каждой дроби найти дополнительный множитель: НОЗ разделить на
знаменатель каждой дроби
умножить числитель и знаменатель каждой дроби на дополнительный
множитель
КОНЕЦ
8

I.7. Классы чисел в школьном курсе математики
|
|
|
Мотивация расширения классов чисел |
|
Дидактиче- |
Математическая |
|
Свойства |
|
Математиче- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(с учётом профиля; |
|
|
|
|
|||
|
Классы |
Реально-кон- |
Геометрическая |
Формально- |
ские замеча- |
|
основа |
|
ская структу- |
||||||||||||||||||||||
|
|
|
для гуманитарного |
||||||||||||||||||||||||||||
|
кретная |
(соответствие |
логическая |
|
|
ния |
|
|
|
|
|
ра (углубление |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
чисел |
(практичес- |
между точками |
(потребности |
|
|
|
|
|
|
- содержательный |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
знаний) |
|
|||||||||||||||||||
|
|
и числами) |
|
математики) |
|
|
|
|
|
|
|
|
|
|
уровень) |
|
|
|
|||||||||||||
|
|
кая) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. |
Натуральные |
счёт, измерение |
|
|
|
|
|
|
|
|
|
усвоение |
|
|
Аксиоматическая |
тео- |
1) |
бесконечность |
|
Полукольцо |
с |
||||||||||
|
числа N |
|
величин |
|
|
|
|
|
|
|
|
|
свойств |
|
|
(ис- |
рия натуральных чисел |
2) |
упорядоченность |
нейтральным |
|||||||||||
|
(1 – 5 классы) |
|
|
|
|
|
|
|
|
|
|
|
|
|
пользование |
на |
(Дж. Пеано, 1891; К. |
3) |
дискретность |
|
) |
элементом |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
содержательном |
Вейерштрасс, 1878; Г. |
4) |
замкнутость (+, |
умножения и без |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уровне |
системы |
Грассман, 1861) |
|
5) |
ограниченность |
|
нейтрального |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аксиом Пеано) |
|
|
|
|
|
снизу |
|
|
элемента сложе- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния |
|
|
|
2. Положитель- |
деление целого |
существование |
математиче- |
1) деление «аб- |
Множество |
упорядо- |
1) |
бесконечность |
|
|
|
|
|
||||||||||||||||||
|
ные дроби |
на части, изме- |
на |
|
числовом |
ское |
выраже- |
страктного |
|
ченных пар натураль- |
2) |
упорядоченность |
|
|
|
|
|||||||||||||||
|
(5 – 6 классы) |
рение величин: |
луче, |
|
точек, |
ние результа- |
целого» |
|
на |
ных чисел: |
|
|
3) |
плотность |
|
|
|
|
|
|
|||||||||||
|
|
длина |
|
отрезка |
которым |
|
не |
та |
деления |
равные |
|
части; |
< a, b > |
|
|
4) |
замкнутость |
|
|
|
|
|
|
||||||||
|
(выделены |
должна |
выра- |
соответствуют |
любых |
нату- |
2) упражнения, |
|
|
|
|
|
(+,·, :) |
|
|
|
|
|
|
||||||||||||
|
жаться |
числом |
известные |
уче- |
ральных |
чи- |
иллюстрирую- |
|
|
|
|
5) |
ограниченность |
|
|
|
|
|
|||||||||||||
|
в дидактичес- |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
(каким?) |
никам числа |
сел |
|
|
|
щие |
свойство |
|
|
|
|
|
снизу |
|
|
|
|
|
|
|||||||||||
|
ких целях) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плотности; |
3) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
алгоритмы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. |
Целые |
характеристика |
существование |
математиче- |
1) практические |
Множество |
пар |
нату- |
1) |
бесконечность |
|
Минимальное |
|||||||||||||||||||
|
числа Z |
изменения ве- |
на |
|
числовой |
ское |
выраже- |
задачи, |
|
приво- |
ральных чисел |
|
2) упорядоченность |
кольцо, |
являю- |
||||||||||||||||
|
(6 класс) |
личин (tº, высо- |
прямой |
точек, |
ние результа- |
дящие к появле- |
|
(Карл |
Теодор |
3) |
дискретность |
|
|
щееся |
расшире- |
||||||||||||||||
|
|
та над уровнем |
которым |
|
не |
та вычитания |
нию |
новых |
чи- |
Вильгельм |
Вейер- |
4) |
замкнутость |
|
|
нием полукольца |
|||||||||||||||
|
|
моря, движение |
соответствуют |
любых |
нату- |
сел; 2) алгорит- |
штрасс, 1878) |
|
|
(+, ·, ─) |
|
|
натуральных |
|
|||||||||||||||||
|
|
в |
противопо- |
известные |
уче- |
ральных |
чи- |
мы |
выполнения |
|
5) неограниченность |
чисел |
|
|
|||||||||||||||||
|
|
ложных напр.) |
никам числа |
сел |
|
|
|
действий |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Действительные |
1) обобщение понятия рационального числа с иллюстрацией прин- |
1) |
Бесконечные |
1) |
бесконечность |
Q - минимальное |
|||||||||||||||||||||||||
|
числа R |
ципов |
|
расширения |
одного |
числового множества |
до другого; 2) |
десятичные дроби (К. |
2) |
упорядоченность |
поле, являющее- |
||||||||||||||||||||
|
|
представление бесконечной десятичной периодической дроби в |
Вейерштрасс, 1872) |
3) |
плотность |
|
|
ся |
расширением |
||||||||||||||||||||||
4. |
Рациональные |
виде обыкновенной; 3) иллюстрация свойств множества рацио- |
2) |
Фундамен- |
4) |
замкнутость |
отно- |
кольца |
целых |
||||||||||||||||||||||
нальных чисел (на содержательном уровне) на примерах |
|
|
|
|
тальные |
последова- |
|
сительно |
|
всех |
чисел |
|
|
||||||||||||||||||
|
числа Q |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Практические |
«построение» |
Решение |
урав- |
Алгоритм |
из- |
тельности |
рациональ- |
|
арифметических |
R – алгебраичес- |
||||||||||||||||||||
|
(9 класс) |
|
|||||||||||||||||||||||||||||
5. |
задачи, |
|
приво- |
на |
|
числовой |
нений |
вида: |
х2 |
влечения |
кор- |
ных чисел (Георг Кан- |
|
операций и |
опера- |
кая |
система |
с 2- |
|||||||||||||
Иррациональ- |
дящие к состав- |
прямой |
точек, |
= b, где b не |
ня квадратного |
тор, 1879) |
|
|
|
ции извлечение из |
мя |
бинарными |
|||||||||||||||||||
|
ные числа I |
|
|
|
|||||||||||||||||||||||||||
|
лению |
квадрат- |
соответствую- |
является |
точ- |
из |
рациональ- |
3) |
Сечения |
в по- |
|
корня из неотрица- |
операциями. |
Ак- |
|||||||||||||||||
|
(8, 10 классы) |
ных |
уравнений, |
щих |
иррацио- |
ным квадратом |
ного числа |
|
ле |
действительных |
|
тельного числа |
|
сиомы: |
поля, |
||||||||||||||||
|
|
где D - не точ- |
нальным |
|
чис- |
b>0); |
|
|
|
|
|
|
|
|
чисел (Рихард Деде- |
5) |
неограниченность |
порядка, |
Архиме- |
||||||||||||
|
|
ный квадрат |
лам |
|
|
|
|
|
|
|
|
|
|
|
|
кинд, 1872) |
|
|
|
|
|
|
да, полноты |
|
|||||||
6. |
Комплекс- |
Дж. |
Кардано, |
установление вза- |
выразить |
ре- |
Решение |
зада- |
1) геометрическая инте- |
Поле С алгебраиче- |
Минимальное по- |
||||||||||||||||||||
ные числа С (10 |
1545; Л. Эйлер, |
имно-однозначн. |
зультат |
|
из- |
чи, |
приводя- |
претация: |
Вессель, |
ски замкнуто, т.е. |
ле, |
являющееся |
|||||||||||||||||||
или 11 класс, ест.- |
Ж. Д’Аламбер, |
соответств. |
меж- |
влечения кор- |
щей к квадрат- |
Арган, Гаусс; 2) пары |
любой многочлен с |
расширением по- |
|||||||||||||||||||||||
мат. профиль) |
К. Гаусс, 1799; |
ду |
числами и |
ня |
чётной |
ному |
уравне- |
действительных чисел и |
коэффициентами |
из |
ля |
действитель- |
|||||||||||||||||||
использование |
точками |
«число- |
степени |
|
из |
нию с D< 0 |
|
векторная интерпрета- |
С разлагается на ли- |
ных чисел с эле- |
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
в мат. физике |
вой плоскости» |
числа а, а<0 |
|
|
|
|
|
ция (Гамильтон, 1837) |
нейные множители |
ментом i,: i2 = - 1 |
|||||||||||||||||||
9

I.8. Методическая схема обучения отдельному классу чисел
Используя необходимый учебник и таблицу 1.7. организовать обучение конкретному классу чисел в следующей последовательности:
а) мотивация расширения известного числового множества; б) анализ случая неразрешимости уравнения в известном числовом множестве;
в) понятие новых чисел (присоединение новых чисел к известным); г) сравнение новых чисел и округление (если возможно); д) действия (операции) с новыми числами;
е) применение новых чисел (возвращение к первоначальному уравнению и его решение); ж) иллюстрация принципов расширения одного множеств до другого;
з) иллюстрация свойств числовых множеств; и) предъявление сведений из истории математики (например, первый кризис в ма-
тематике при изучении иррациональных чисел); к) решение различных типов задач на новом числовом множестве.
I.9. Алгебраические структуры
1.Кольцо
Некоторое множество, на котором заданы две функции, одна из которых называется сложением, а вторая – умножением, причём для любых а, b, с из этого множества сложение и умножение подчиняются аксиомам кольца* (1):
8) а · 1 = а
* Замечания: а) точнее, коммутативное и ассоциативное кольцо; б) свойства 6) и 7) иногда не включают в систему аксиом кольца.
2.Поле
Множество, являющееся кольцом, на котором выполняется аксиома: 9) для любого а ≠ 0 существует число, называемое обратным ему и обозначаемое 1/а, для которого а·1/а = 1. Число а·1/b, b ≠ 0, называется частным от деления а на b и обозначается а/b.
3.Группа
Непустое множество G называется группой, если в нем определена алгебраическая операция *, которая каждым двум элементам a, b из G ставит в соответствие элемент a * b также из G, причём операция * обладает свойствами:
1)для любых а, b, с из G: a * (b * c) = (a * b) * c – ассоциативность операции *;
2)в G существует нейтральный элемент е, такой, что: а * е = а;
3)в G существует элемент – а, такой что: а * (-а) = е – обратимость
Если групповая операция * коммутативна, т. е. a * b = b * a для любых a, b из G, то группа G называется коммутативной или абелевой. Множества: целых, рациональных, действительных и комплексных чисел являются группами относительно операции сложения чисел, играющей роль групповой операции *. Множества: рациональных, действительных и комплексных чисел без числа 0, образуют группу относительно операции умножения чисел, играющей роль групповой операции *.
10
