Kalney_Limits_Continuos

Раздел I. Математический анализ

Глава 1. Предел и непрерывность

1.1. Действительные числа. Свойства действительных чисел

Понятие числа является одним из основных в математике и из школьного кур-

са математики известно, что, начиная с древности, оно неоднократно подвергалось расширению и обобщению. В данной книге не излагается строгая теория действи-

тельных чисел. Напоминаются лишь основные факты, обозначения, а также свойст-

ва действительных чисел.

Множество натуральных чисел {1, 2, 3,...} обозначается буквой N , а множе-

ство целых чисел {..., − 2, −1, 0, 1, 2, ...} – Z . Множество рациональных чисел, т.е.

дробей вида m , где m целое число, а n натуральное число, обозначается буквой n

Q . Множество N есть подмножество множества Z , и, в свою очередь, Z Q .

Рассмотрим числовую прямую, т. е. прямую, на которой отмечено начало от-

счета точка O , выбраны единичный отрезок OE и положительное направление от точки O к точке E .

Каждому рациональному числу соответствует единственная точка на число-

вой прямой. Вместе с тем не каждой точке на числовой прямой соответствует ра-

циональное число. Например, точке A на прямой такой, что длина отрезка OA рав-

на длине диагонали квадрата с единичной стороной, не может быть поставлено в со-

ответствие какое-либо рациональное число. Другими словами, не все отрезки будут иметь длину, если пользоваться только рациональными числами. В области рацио-

нальных чисел не существует квадратных корней из чисел 2 или 3 (и многих дру-

гих). Поэтому для успешного решения многих задач множество рациональных чисел необходимо расширить.

Действительными (вещественными) числами будем называть бесконечные де-

сятичные дроби

1

где a0 – целое неотрицательное число, a1, a2 , a3 ,...– десятичные цифры 0, 1, …, 9.

Любому рациональному числу m соответствует бесконечная периодическая n

дробь вида (1.1), которую легко получить, выполняя деление числа m на n «угол-

ком». И обратно, любая бесконечная периодическая дробь с помощью формулы суммы бесконечно убывающей геометрической прогрессии может быть заменена

дробью вида m . При этом считается, что конечная десятичная дробь n

±a0 , a1a2a3...ak может быть записана как бесконечная ±a0 , a1a2a3...ak 00..., а так-

же, что выполняется равенство ±a0 , a1a2a3...(ak −1)99... .= ±a0 , a1a2a3...ak 00....

Произвольная бесконечная непериодическая дробь вида (1.1) называется ирра-

циональным числом. Иррациональными, как известно со школы, являются числа

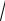2 = 1, 4142... , π = 3,1415.... Легко привести другие примеры иррациональных чи-

сел. Например, иррациональным числом будет непериодическая дробь 1,101001....

Далее действительные числа будут обозначаться одной буквой: a , b , α и т.д..

Множество всех действительных чисел обозначается буквой R .

Для действительных чисел вводятся отношения «равно» ( =), «больше» ( > ) и «меньше» ( < ), а также операции сложения и умножения, которые удовлетворяют следующим пяти группам свойствам.

1. Свойства порядка.

1.1.Для каждой пары чисел a и b выполнено одно и только одно отноше-

ние: a = b , a > b , a < b (любые два действительных числа сравнимы между собой).

1.2.Из отношений a < b и b < c следует, что a < c (транзитивность отно-

шения меньше; аналогичное свойство верно и для отношения больше).

1.3.Если a < b , то существует такое число c , что a < c < b (свойство плот-

ности).

2. Свойства сложения.

2.1. a + b = b + a для любых a и b (коммутативность сложения).

2

2.2.(a + b) + c = a + (b + c) для любых a , b и c (ассоциативность сложе-

ния).

2.3.a + 0 = a для любого a (особая роль числа ноль).

2.4.Для каждого числа a существует такое число −a , что a + (−a) = 0 .

Число −a называют противоположным данному числу. На основе этих свойств сложения может быть введена операция вычитания. Вычесть из числа a

число b это значит прибавить к числу a число, противоположное числу b :

a − b = a + (−b) .

2.5.Если a < b , то a + c < b + c для любого числа c (знак неравенства со-

храняется, если к обеим частям неравенства прибавить одно и то же число).

3. Свойство умножения.

3.1.ab = ba для любых a и b (коммутативность умножения).

3.2.(ab)c = a(bc) для любых a , b и c (ассоциативность умножения).

3.3.a 1 = a для любого a (особая роль числа один).

Число 1 называют обратным данному числу. На основе этих свойств умно- a

жения может быть введена операция деления. Разделить число a на число b ≠ 0 это

значит умножить число a на число, обратное числу b , т.е.: a = a 1 . b b

3.5.(a + b)c = ac + bc для любых a , b и c (дистрибутивность умножения

относительно сложения)

3.6.Если a < b , то ac < bc для любого числа c > 0 (знак неравенства сохра-

няется, если обе части неравенства умножить на одно и то же положительное чис-

ло).

4.Свойство Архимеда. Для любого положительного числа c найдется на-

туральное число n такое, что n > c .

5.Свойство непрерывности (полноты). Если последовательность действи-

тельных чисел не убывает и ограничена сверху (т. е. существует такое число, что

3

любой член последовательности не больше этого числа), то она стремится к некото-

рому пределу (подробнее см. ниже пп. 1.4, 1.8).

Поясним это свойство. Пусть имеем последовательность неотрицательных чи-

сел. Тогда целые части членов последовательности также не убывают и ограничены сверху. Поэтому, начиная с некоторого номера m0 , целые части членов последова-

тельности не будут меняться. Обозначим это целое неотрицательное число как α0 .

Первые десятичные знаки членов последовательности с номерами большими, чем m0 , не убывают. Так как десятичных знаков лишь конечное число значений, то, на-

чиная с некоторого номера m1 ≥ m0 , они станут принимать одно и то же значение

α1. Рассуждая аналогично далее, получим в результате число +α0 , α1α2 ... , которое и будет пределом заданной последовательности.

Свойство непрерывности обеспечивает возможность установления взаимно-

однозначного соответствия между множеством действительных чисел и точками не-

прерывной числовой прямой: каждому действительному числу соответствует един-

ственная точка на прямой и, наоборот, каждой точке соответствует единственное действительное число. В силу этого, во многих рассуждениях будут равнозначно употребляться выражения «возьмем число a » и «возьмем точку a ».

Свойство непрерывности может быть сформулировано также в следующих эк-

вивалентных, интуитивно ясных, формах.

Пусть даны два отрезка [a, b] и [c, d ]. Если a ≤ c ≤ d ≤ b , то говорят, что от-

резок [c, d ] вложен в отрезок [a, b] .

Если задана последовательность вложенных друг в друга отрезков, длины которых стремятся к нулю, то существует точка, притом единственная, принад-

лежащая всем отрезкам одновременно. Это утверждение называется принципом вложенных отрезков.

Рассмотрим непустое числовое множество E . Если существует число a , при-

надлежащее множеству E , такое, что x ≤ a для любого x E , то число a называют

наибольшим (максимальным) элементом (значением) множества E : a = max E =

4

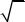
= max x . Аналогично, если для a E и любого числа x E выполнено неравенст-

x E

во x ≥ a , то a называют наименьшим (минимальным) элементом множества E :

a = min E = min x .

x E

Если множество содержит конечное количество элементов, то в нем есть мак-

симальный и минимальный элементы. Если множество содержит бесконечное число элементов, то оно может и не иметь максимального (минимального) элементов. На-

симального элементов.

Вместе с тем, пусть непустое множество E ограничено сверху, т.е. существу-

ет число K такое, что любого числа x E выполнено неравенство x ≤ K . Число K

называют верхней границей (гранью) множества E . Ясно, что любое число, большее

K , также будет верхней границей множества E . Однако не любое число, меньшее

K , также будет верхней границей множества. Число, меньшее любого элемента из

E , уже не является верхней границей.

Число M , равное наименьшей из верхних граней множества E называется

точной верхней гранью множества E и обозначается M = sup E = sup x (читается

x E

«супремум»).

Всякое непустое ограниченное сверху множество имеет точную верхнюю грань. Это утверждение называют теоремой о существовании точной верней грани у ограниченного сверху множества.

Множество рациональных чисел удовлетворяет всем свойствам 1-4 групп. Од-

нако оно не удовлетворяет свойству непрерывности.

Например, возьмём иррациональное число 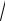2 =1, 4142... . Рассмотрим возрас-

тающую последовательность рациональных чисел: x1 =1, x2 =1, 4 , x3 =1, 41 и т.д..

Тогда эта последовательность не убывает, ограничена сверху (например, числом 2),

но не стремится ни к какому рациональному числу.

5

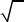
Для множества чисел E = {1; 1, 4; 1, 41;...} не существует наименьшего рацио-

нального числа, ограничивающего любой элемент из E .

Рассмотрим последовательность отрезков [1, 2] , [1, 4; 1, 5] , [1, 41; 1, 42] , ….

Они вложены друг в друга, длины их стремятся к нулю. Однако если рассматривать только рациональные числа, принадлежащие отрезкам, то общей точки у отрезков не

будет (общая точка иррациональное число 2 ).

1.2. Понятие функции. Способы задания функции

1. Понятие функции

Понятие функции, то есть зависимости одних переменных величин от других,

является одним из основных в математике и формировалось в течение нескольких последних столетий. Приводимое ниже определение понятия функции (точнее чи-

словой функции одной переменной) сформулировали в 19 веке математики Н.И. Ло-

бачевский и П.Г.Л. Дирихле.

Пусть задано множество D действительных чисел. Если каждому числу x D поставлено в соответствие действительное число y , то говорят, что на мно-

жестве D задана функция. Переменную x называют аргументом или независимой

переменной, а y зависимой переменной или функцией.

Если правило соответствия обозначить через f , то пишут y = f ( x) . Эта за-

пись понимается двояко. С одной стороны, считая x произвольным из D , её пони-

мают как обозначение функции. С другой стороны, её понимают и как указание, что определённому, фиксированному числу x поставлено в соответствие определённое число y .

Для обозначения функции могут применяться и другие буквы, например:

y= g ( x) , y = F ( x) , s = ϕ(t) .

Вматематическом анализе изучаются также функции, когда одному значению независимой переменной x ставится в соответствие несколько (даже может быть бесконечное число) значений y . Такие функции называют многозначными, в отли-

чие от определенной выше однозначной функции. В дальнейшем, мы будем рас-

6

сматривать однозначные функции. Случаи рассмотрения многозначных функций

будут оговариваться особо.

Множество D называется областью определения функции, а множество всех

чисел y , которые принимает функция, когда переменная x пробегает все значения

E( f ) B , но не обязательно E( f ) = B .

Областью определения заданной функции может быть вся числовая прямая,

интервал, отрезок, совокупность непересекающихся интервалов, множество только

натуральных чисел и т.д..

Пусть на плоскости задана система координат, например, прямоугольных (де-

картовых). Графиком функции y = f ( x) называют множество точек плоскости с ко-

ординатами ( x, f ( x)) , где x пробегает все значения из области определения. Гра-

фик может быть как непрерывной, так и разрывной кривой, а также набором от-

дельных точек на плоскости, например, когда областью определения функции явля-

ется множество натуральных чисел.

Далее везде, если не оговорено особо, графики функций изображаются в пря-

моугольных координатах.

2. Способы задания функции

Часто применяется аналитический способ, при котором функция задается фор-

мулой, определяющей алгебраические операции и арифметические действия, которые нужно выполнить над переменной x и, возможно, постоянными числами, чтобы по-

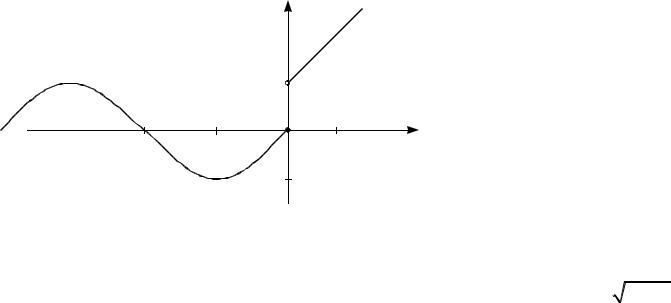
sin x, x ≤ 0,

лучить значение y . Например, s = πr 2 , y = 3log2 ( x2 + 2x + 2) , y =

x + 1, x > 0

(см.рис.1.1).

7

При графическом способе зависимость между переменными выражается в ви-

де множества точек на плоскости с заданной системой координат, например, прямо-

угольных. Так как мы рассматриваем только однозначные функции, то в случае прямоугольных координат никакие две точки не должны лежать на одной прямой,

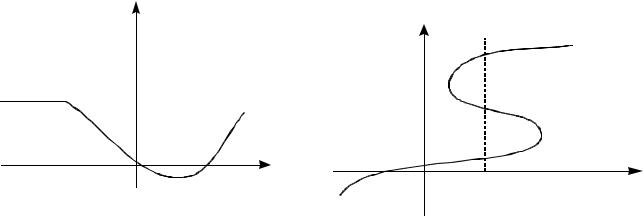
параллельной оси ординат. Поэтому, рисунок 1.2 задаёт графически некоторую од-

нозначную функцию, а рисунок 1.3 – нет.

8

лицы совпадали с табличными значениями y . Методам решения данных задач бу-

дет посвящена значительная часть книги.

3. Сложная и обратная функции

Пусть переменная y зависит от переменной u : y = f (u) . Если переменная u

сама зависит от некоторой переменной x , то есть u = g ( x) , то зависимость пере-

менной y от переменной x , заданную выражением y = f ( g ( x)) , называют слож-

ной функцией, полученную суперпозицией или композицией функций f и g . На-

пример, функцию y = 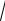1 − 2x можно считать сложной, полагая, y = u и

u = 1 − 2x .

обратной функции формулируется так. Пусть функция y = f ( x) определена на

соответствие то x , для которого y = f ( x) . Таким образом, выполняется тождество

y ≡ f ( f −1( y)) на множестве E( f ) .

Обратная функция может быть многозначной. Например, из уравнения y = x2

для y > 0 находим два значения x = ± y , обладающим требуемым свойством:

y = (± 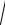y )2 .

Для того, чтобы обратная к y = f ( x) функция была однозначной, необходимо и достаточно, чтобы f (x1) ≠ f ( x2 ) при x1 ≠ x2 .

10