§ 2.2. Непрерывность в точке и на отрезке

2.2.1. Непрерывность функции в точке

Определение. Функция называетсянепрерывной в точке если то есть

Запишем определение непрерывности на языке приращений. Рассмотрим функцию определённую в некоторой окрестности точкии точкуиз этой окрестности.Приращением аргумента называется величина Приращению аргумента соответствует приращение функции Функция непрерывна в точкеесли

Функция непрерывна в точкетогда и только тогда, когда в этой точке существуют односторонние пределы, равные значению в этой точке.

Если то функция называется непрерывной справа в точке еслитонепрерывной слева.

Непрерывные в точке функций обладают всеми свойствами функций, имеющих предел в точке.

Теорема о непрерывности сложной функции. Если функция непрерывна в точкеа функциянепрерывна в точкето сложная функциянепрерывна в точке

Доказательство. Зададим Так как функциянепрерывна в точкето найдётсятакое, что для всехудовлетворяющих неравенствувыполняется неравенствоТак как функциянепрерывна в точкето для этогонайдётсятакое, что для всехудовлетворяющих неравенствувыполняется неравенството естьследовательно,то естьЗначит,непрерывна в точке

Следствие. Если то

Доказательство. Рассмотрим функции прии при Так как функция непрерывна в точке а функциянепрерывна в точкето функция непрерывна в точке

Пример. Функцию можно рассматривать как сложную функциюгдеРанее было доказано, чтото есть функцииинепрерывны в любой точке числовой прямой. Тогда функциятакже непрерывна.

Из доказанных свойств пределов и приведённых примеров следует, что функции (и- многочлены),непрерывны во всех точках области определения.

2.2.2. Первый замечательный предел

Теорема.

Доказательство. Рассмотрим Можно считать, что По ранее доказанному неравенству имеемОтметим на единичной окружности точкиисоответствующие угламии проведём из них касательные, пересекающиеся в точкележащей на осиТогда длина дугиравнаи меньше дины ломанойравнойто есть выполняется неравенствоТогда получаемТак как в силу непрерывности косинусато существует Рассмотрим теперь Сделав замену получим Так как односторонние пределы существуют и равны между собой, то

Следствие. Если то

2.2.3. Второй замечательный предел

По определению числа оно равно пределу последовательностиОднако, не для всякой функциисуществование предела последовательностивлечёт за собой существование пределаНапример, для функциине существует предела пристремящемся к бесконечности, однако последовательностьсходящаяся.

Теорема.

Доказательство. Рассмотрим сначала Можно считать, что Тогда выполняются неравенства (- целая частьт.е. наибольшее целое число, не превосходящее). Получаем

Так как инатуральные, то

Следовательно,

Рассмотрим сделав замену

Следствия.

1. Если то

2. 3.

4.

2.2.4. Бесконечно малые функции

Определение. Функция называетсябесконечно малой при стремящемся кесли

Аналогично определяются функции, бесконечно малые при стремящемся к бесконечности.

Утверждение. тогда и только тогда, когда функцияявляется бесконечно малой пристремящемся к

Если - бесконечно малые притотакже является бесконечно малой при

Если - бесконечно малая приаограниченна в некоторой окрестности точкитоявляется бесконечно малой при

Определение. Две функции иявляющиеся бесконечно малыми приназываютсяэквивалентными при (при), если

При справедливы следующие эквивалентности:

Теорема. Если прии существуют пределыто существуют и пределы

Доказательство.

Если притопри

Если притопри

Пример. Вычислим предел Так как присправедливы эквивалентности:

то

Определение. Пусть даны две бесконечно малые при функции иПорядком малости относительно называется числотакое, чтоЕслито говорят, что является бесконечно малой большего порядка малости, чем или является о-малым от обозначается

Теорема. Две бесконечно малые при функции иэквивалентны тогда и только тогда, когда

Доказательство. При равносильны утверждения:

Функции , бесконечно малые при обычно сравниваются с Функции, бесконечно малые при сравниваются с

Примеры. 1. Найдём порядок бесконечно малой при относительно

при порядок равен 3.

2. Найдём порядок бесконечно малой при относительно

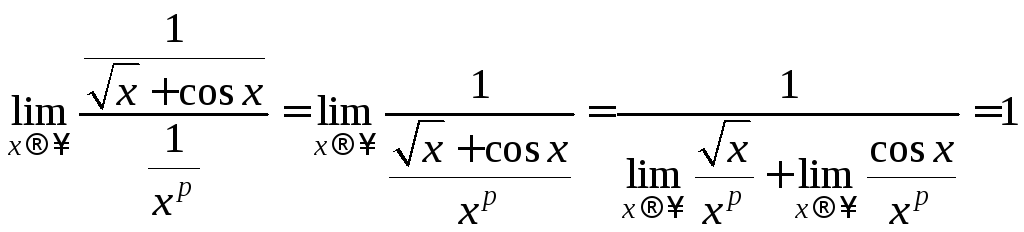
при т.к.как произведение бесконечно малой на ограниченную. Порядок бесконечно малой равен 0,5