Вопросы для самоконтроля

1. Куда направлен момент импульса материальной точкиотносительно неподвижной точки(см. рис. 3 – рисунок выполнен в плоскости листа):

а) на нас; б) от нас; в) лежит в плоскости рисунка 3?

2. Груз массывращается на нити длинойв горизонтальной плоскости (см. рис. 4). Нить образует с вертикалью угол. Чему равны величины моментов силы натяжения нитии силы тяжестиотносительно точки:

а) б)в)г)

д)е)ж)з)?

Укажите правильные утверждения.

3. Груз массы вращается на нити длинойв горизонтальной плоскости (см. рис. 4) со скоростью. Нить образует с вертикалью угол. Чему равны момент силы тяжестии момент импульсагруза относительно оси

а)б)в)г)

д) е)ж)з)

Укажите правильные утверждения.

4. Момент импульса системы материальных точек относительно точки не меняется, если:

а) точка неподвижна;

б) на систему не действуют внешние силы;

в) момент внешних сил равен нулю;

г) центр масс системы неподвижен относительно точки ;

д) система замкнута.

Укажите ошибочные утверждения.

5. Уравнения моментов для системы материальных точек относительно неподвижной точки и движущейся точкиимеют одинаковый вид, если:

а) скорость центра масс системы относительно точки равна нулю;

б) импульс системы относительно точки равен нулю;

в) точка совпадает с центром масс системы;

г) скорости центра масс системы и точки относительно неподвижной точки- коллинеарные векторы.

Укажите правильные утверждения.

Примеры решения задач

Пример 1. Момент импульса частицы относительно некоторой точки меняется со временем по закону гдеи– постоянные векторы, причемНайти относительно точкимомент силыдействующий на частицу, когда угол междуиокажется равным

Р е ш е н и е. Зависимость момента силы от времени найдем, воспользовавшись уравнением моментов (4) для одной материальной точки

(16)

Взаимное расположение векторов ив тот момент времени, когда угол между ними станет равенпоказано на рис. 5. Из рисунка видно, что

.

Определяя из этого уравнения и подставляя в (16), найдем момент силы относительно точкив этот момент времени

.

Пример 2.Шайба массойскользя по гладкой горизонтальной поверхности со скоростьюиспытала в точке(рис. 6) упругое столкновение с гладкой неподвижной стенкой. Угол между направлением движения шайбы и нормалью к стенке равен. Найти:

а) точки, относительно которых момент импульса шайбы остается постоянным в этом процессе;

б) модуль приращения момента импульса шайбы относительно точки которая находится в плоскости движения шайбы на расстоянииот точки

Р е ш е н и е.а) Из уравнения моментов (4) следует, что момент импульса будет оставаться постоянным относительно тех точек, относительно которых момент сил, действующих на шайбу, равен нулю.

В процессе движения на шайбу действуют сила тяжести и сила реакции опоры, которые перпендикулярны плоскости рисунка (на рис. 6 не показаны). Эти силы равны по величине и противоположны по направлению и лежат на одной прямой, поэтому суммарный момент этих сил относительно любой точки будет равен нулю.

В процессе столкновения стенка действует на шайбу с силой , направление которой показано на рис. 6. Момент этой силы будет равен нулю относительно точек, лежащих на прямой, перпендикулярной к стенке и проходящей через точку. Это означает, что момент импульса шайбыбудет оставаться постоянным относительно точек, лежащих на этой прямой.

б) Запишем уравнение (4) в виде

где – вектор, проведенный из точкив точку приложения силыИз этого выражения следует, что момент импульса получает приращение только в процессе соударения шайбы со стенкой.

Из второго закона Ньютона следует, что где– приращение импульса шайбы, поэтому последнее выражение принимает вид

.

Проинтегрировав правую и левую части этого уравнения, получим

,

где и– приращения момента импульса и импульса шайбы в процессе удара. Так как векторколлинеарен вектору онперпендикулярен вектору Учитывая это, модуль приращения момента импульса равен

. (17)

Найдем модуль приращения импульса шайбы в процессе удара. Учитывая, что

где и– импульсы шайбы до и после удара, получим (см. рис. 7)

Так как и, получим

.

Выражая из этого уравнения и подставляя в (17), найдем модуль приращения момента импульса шайбы относительно точки

.

Величину изменения момента импульса можно найти иначе. Изменение момента импульса относительно точкирано

гдеи– моменты импульса шайбы до и после удара о стенку относительно точки. Как следует из определения момента импульса материальной точки относительно неподвижного начала, эти моменты направлены в противоположные стороны (перпендикулярно плоскости рисунка), а их величины (см. рис. 8) равны

т.е. модуль приращения момента импульса шайбы относительно точки равен

Пример 3. Небольшую шайбу поместили на внутреннюю гладкую поверхность неподвижного круглого конуса (рис. 9а) на высоте от его вершины и сообщили ей в горизонтальном направлении по касательной к поверхности конуса скоростьНа какую высоту(от вершины конуса) поднимется шайба?

Р е ш е н и е. Так как внутренняя поверхность конуса гладкая, полная механическая энергия шайбы в процессе движения не меняется

(18)

где – скорость шайбы на высоте. Для нахождения этой скорости воспользуемся уравнением моментов (6) относительно оси. При движении на шайбу действуют две силы (рис. 9б) – сила тяжестии сила реакции опорыМоменты этих сил относительно оси равны нулю. Это означает, что момент импульса шайбы (относительно оси) в процессе движения остается постоянным, т.е.

или

где и– расстояния от оси до шайбы в начальный и конечный моменты времени. Подставляя это выражение в (18), и учитывая, что (см. рис.9а)

получим

откуда находим высоту, на которую поднимется шайба

.

Пример 4. На гладкой горизонтальной плоскости движется небольшое тело массы привязанное к нерастяжимой нити, другой конец которой втягивают в отверстие(рис. 10) с постоянной скоростью. Найти силунатяжения нити в зависимости от расстояниятела до отверстия, если приугловая скорость тела была равна.

Ре ш е н и е.Поскольку суммарный момент сил, действующих на тело, относительно точки равен нулю, момент импульса тела относительно той же точки сохраняется:

(19)

где – угловая скорость тела в тот момент времени, когда оно находится на расстоянииот точки.

При движении тела по плоскости его скорость имеет две составляющие – , направленную вдоль нити, и, направленную перпендикулярно к ней. Первая составляющая по условию задачи в процессе движения не меняется по величин (), вторая () изменяется, так как величины угловой скоростии расстояниетела до точкименяются с течением временем.

Пусть за малый промежуток времени расстояние между телом и осью вращения изменится на малую величину(), тогда по теореме об изменении кинетической энергии

или, с учетом (19),

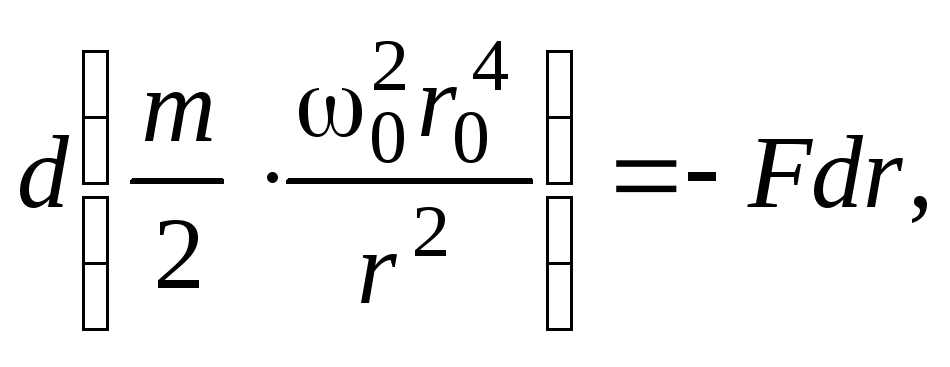
откуда находим зависимость силы натяжения нити от

Пример 5. Шарик массы двигавшийся со скоростью, испытал упругое лобовое соударение с одним из шариков покоившейся жесткой гантели, как показано на рис. 11. Масса каждого шарика гантели равнарасстояние между ними –Пренебрегая размерами шариков, найти величину собственного момента импульсагантели после соударения, т.е. момент импульса в системе отсчета, связанной с центром масс.

Ре ш е н и е. Пусть: а) налетающий шарик после удара движется в прежнем направлении со скоростьюб) центр масс гантели, который в начальный момент времени совпадает с неподвижной точкойпосле удара движется со скоростьюв) шарикигантели относительно центра масс начинают вращаться с угловой скоростью

Учитывая, что данная система частиц замкнута и удар упругий, для решения задачи используем все законы сохранения – закон сохранения импульса, закон сохранения момента импульса и закон сохранения механической энергии.

Запишем закон сохранения импульса в проекции на ось

(20)

Второе слагаемое в правой части этого уравнения это импульс гантели после удара. Действительно, импульс системы материальных точек (гантели) равен произведению массы всей системы на скорость центра масс.

Закон сохранения момента импульса относительно неподвижной точки имеет вид

(21)

При записи этого закона учтено, что импульс гантели направлен вдоль оси , т.е. он коллинеарен радиус-вектору, характеризующему положение центра масс гантели относительно точкиИз уравнения (12) следует, что в этом случае момент импульса гантели относительно точкисовпадает с собственным моментом импульса.

Закон сохранения энергии в неподвижной системе отсчета, связанной с точкой можно записать в виде

,

где – скорость шарика гантели относительно центра масс. В этом выражении величина, стоящая в скобках, это кинетическая энергия гантели после удара. При записи выражения для этой энергии использована теорема Кенига (см. например учебник – Д.В. Сивухин “Механика” том 1 ), согласно которойкинетическая энергия системы частиц равна сумме кинетической энергии системы частиц в системе отсчета, связанной с центром масс (),и кинетической энергии системы как целого ().

Выразим кинетическую энергию гантели в системе отсчета, связанной с центром масс, через собственный момент импульса. Величина собственного момента импульса гантели равна

Возведем правую и левую части этого уравнения в квадрат

откуда

.

С учетом этого закон сохранения энергии перепишем в виде

(22)

Решая совместно уравнения (20) ÷ (22), можно найти собственный момент импульса гантели однако решение этой системы уравнений достаточно сложная математическая задача, поэтому рассмотрим наиболее простой способ ее решения.

Перепишем уравнения (22) и (21) в виде

Разделим первое уравнение на второе

(23)

Из уравнений (20) и (21) следует, что

Подставляя это выражение в (23), получим

(24)

Решая совместно уравнения (21) и (24), найдем собственный момент импульса гантели

Пример 6. На гладкой горизонтальной плоскости лежат две небольшие одинаковые шайбы, каждая массы Шайбы соединены легкой недеформированной пружиной, длина которойи жесткостьВ некоторый момент одной из шайб сообщили скоростьв горизонтальном направлении перпендикулярно к пружине. Найти максимальное относительное удлинение пружинки в процессе движения, если известно, что оно значительно меньше единицы.

Р е ш е н и е. Относительно плоскости шайбы будут совершать сложное движение. После того, как одной из шайб сообщили скорость, центр масс системы начнет двигаться поступательно с некоторой скоростьюотносительно плоскости, а шайбы начнут вращаться и совершать колебания относительно центра масс. Для того, чтобы упростить решение задачи, исключим поступательное движение шайб, т.е. решим задачу в системе отсчета, связанной с центром масс.

Шайбы можно рассматривать как замкнутую систему тел, между которыми действует упругая сила, поэтому для решения задачи воспользуемся законами сохранения энергии и сохранения момента импульса.

Найдем скорости шайб относительно центра масс в начальный момент времени. Для этого определим сначала скорость центра масс относительно плоскости. Так как импульс системы материальных точек равен произведению массы системы на скорость центра масс

получим

Используя формулу преобразования скоростей , гдеи– скорости шайб относительно неподвижной и подвижной систем отсчета, найдем, что скорости шайб относительно центра масс в начальный момент времени направлены в противоположные стороны, перпендикулярны к пружине и равны

(25)

Так как в системе отсчета, связанной с центром масс, импульс системы равен нулю, скорости шайб в каждый момент времени будут равны по величине и направлены в противоположные стороны, поэтому закон сохранения энергии можно записать в виде

(26)

где и– скорость одной из шайб относительно центра масс и удлинение пружины в произвольный момент времени.

Направление скорости относительно пружины в процессе движения будет меняться, т.к. эта скорость является суммой двух скоростей – скорости колебательного и скорости вращательного движения шайбы относительно центра масс. Однако в те моменты времени, когда удлинение пружины будет максимально, скорость колебательного движения будет равна нулю, и скоростьбудет перпендикулярна к пружине.

Рассматривая этот момент времени как конечный, закон сохранения момента импульса можно записать в виде

,

где – максимальное удлинение. По условию задачи<< 1, поэтому последнее уравнение преобразуем к виду

(27) Решая совместно уравнения (25) ÷ (27) получим

.

Учитывая опять, что << 1, т.е.найдем максимальное относительное удлинение пружины