
- •§1. Экспериментальные основы квантовой механики
- •§2. Классическое и квантовое описание системы
- •§3. Принцип неопределенности
- •§4. Полный набор динамических переменных
- •§5. Постулаты квантовой механики
- •§7. Волновая функция и ее свойства
- •§10. Операторы в квантовой механике
- •Транспонированный оператор
- •§11. Собственные функции и собственные значения эрмитовых операторов. Случай дискретного и непрерывного спектра
- •§12. Среднее значение измеряемой величины
- •§13. Вероятность результатов измерения
- •§15. Операторы координаты , импульса, момента импульса, энергии
- •§ 19 Волновое уравнение
- •§ 24 Оператор Гамильтона различных систем
- •§ 26. Решение волнового уравнения в случае свободной материальной точки
- •§ 27. Решение волнового уравнения в случае бесконечно глубокой потенциальной ямы
- •§ 36. Собственный механический момент (спин)
§12. Среднее значение измеряемой величины
По определению
![]() (12.1)
(12.1)
Рассмотрим оператор
![]() с дискретным спектром. Разложим
с дискретным спектром. Разложим![]() по собственным функциям оператора
по собственным функциям оператора![]() :
:
![]() (12.2)
(12.2)
По равенству Парсеваля
![]() .
.
![]()
Т.к. оператор линейный, то его можно занести под знак суммы:
![]()
![]()
![]() (12.3)
(12.3)
Подставляя (12.3) в числитель, а (12.2) в знаменатель для (12.1), имеем
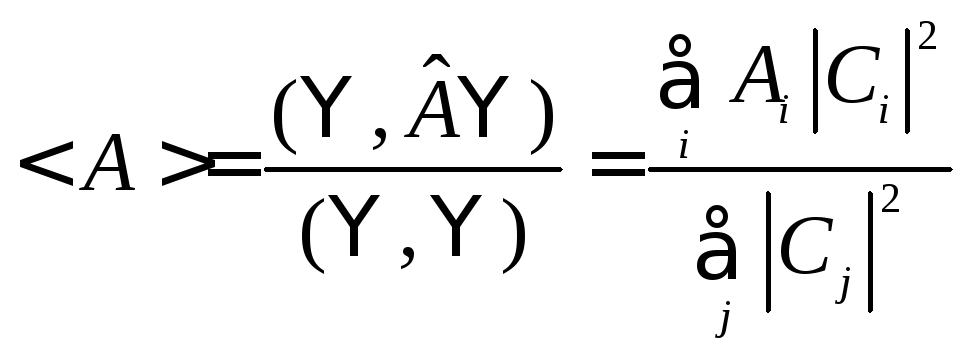
Из теории вероятности
![]() ,
где
,
где![]() - вероятность получения
- вероятность получения![]() ,
тогда
,
тогда
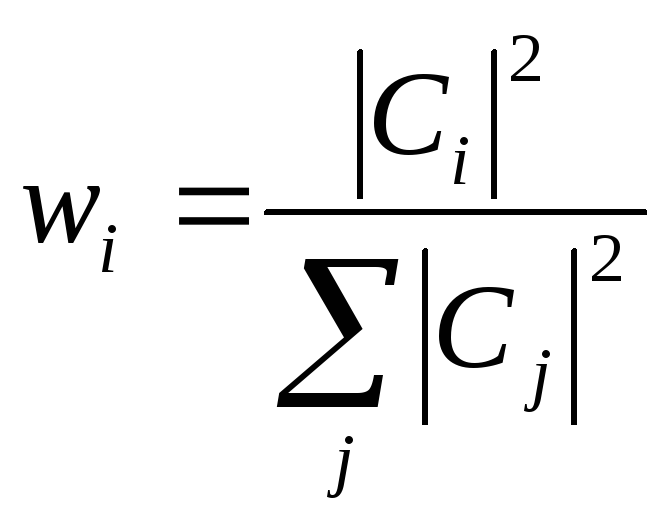
§13. Вероятность результатов измерения
Пусть
![]() - вероятность того, что при измерении
величины
- вероятность того, что при измерении
величины![]() для системы, находящейся в состоянии
для системы, находящейся в состоянии![]() мы получим результат
мы получим результат![]() .
Если система находится в состоянии
.
Если система находится в состоянии![]() ,
то величина
,
то величина![]() при измерении выходит с вероятностью
равной 1:
при измерении выходит с вероятностью
равной 1:
![]()
В общем случае;
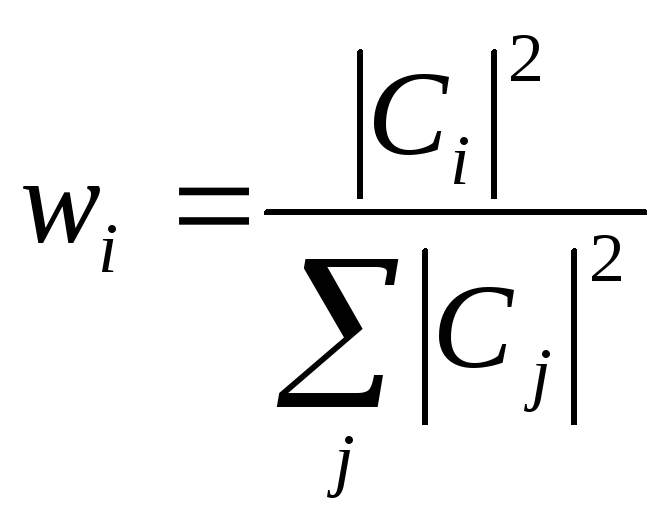
Если полная производная оператора
![]() удовлетворяет
равенству
удовлетворяет
равенству
![]() ,
,
то собственная функция оператора
![]() описывает состояние системы.
описывает состояние системы.
Для непрерывного спектра, вероятность
того, что результаты измерения величины
Aдля системы, находящейся
в состоянии![]() ,
лежит в интервале от
,
лежит в интервале от![]() до
до![]() ,
определяется следующим выражением:
,
определяется следующим выражением:
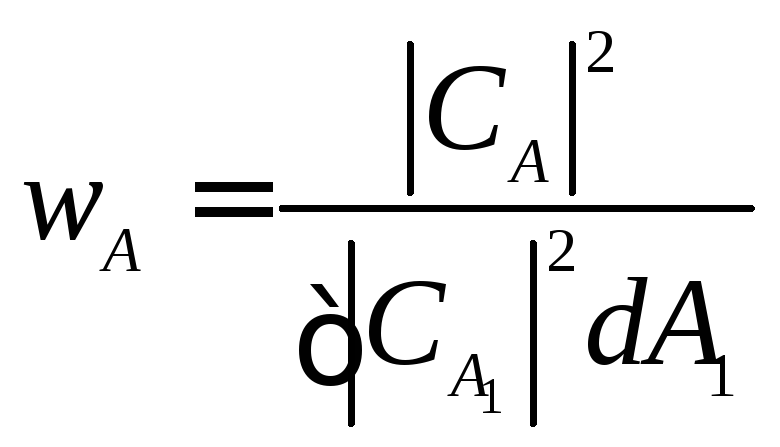 ,
,![]() (13.1)
(13.1)
или плотность вероятности
![]()
§15. Операторы координаты , импульса, момента импульса, энергии
Будем использовать координатное
представление (![]() -представление). Будем рассматривать
систему из одной материальной точки.
Действие
-представление). Будем рассматривать
систему из одной материальной точки.
Действие
![]() сводится к умножению на вектор
сводится к умножению на вектор
![]() ,
т. е.
,
т. е.![]() (это определение действия оператора
(это определение действия оператора
![]() ).
).
![]()
![]()
Здесь строго соблюдается последовательность операторов при раскрытии векторного произведения, например, первая компонента:
![]() ,
,
однако для частного случая декартовых координат порядок операторов не существенен.
Оператор энергии или гамильтониан
![]() :
:
![]() ,
,
здесь
![]() -
оператор кинетической энергии,
-
оператор кинетической энергии,![]() - оператор потенциальной энергии. Для
одной материальной точки гамильтониан
имеет вид:
- оператор потенциальной энергии. Для
одной материальной точки гамильтониан
имеет вид:
![]()
![]()
Переменная t – признак внешнего нестационарного поля.
![]()
Тут присутствует
![]() и
и
![]() ,
но
,
но![]() и
и![]() одновременно неизмеримы, тогда
потенциальная и кинетическая энергия
в квантовой механике не могут быть
одновременно измеримыми. В квантовой
механике существует понятие “энергия
частицы”, но порознь вводить энергию
нельзя, иначе либо
одновременно неизмеримы, тогда
потенциальная и кинетическая энергия
в квантовой механике не могут быть
одновременно измеримыми. В квантовой
механике существует понятие “энергия
частицы”, но порознь вводить энергию
нельзя, иначе либо![]() ,
либо
,
либо![]() оказываются
неизвестными.
оказываются
неизвестными.
§ 19 Волновое уравнение
Надо сформулировать уравнение функции, которая описывала бы квантово-механическую систему.
Это уравнение было получено Шредингером интуитивным путем. Оно ниоткуда не выводится.
Приведем некоторые соотношения в пользу уравнения Шредингера:
Норма волновой функции:
![]()
![]() - вероятность обнаружить динамические
переменные в интервале
- вероятность обнаружить динамические
переменные в интервале![]() .
.
Наложим на
![]() - условие ее сохранения во времени.
- условие ее сохранения во времени.![]() - это физическое требование, поскольку
- это физическое требование, поскольку![]() ,
то
,
то![]() также
функция времени.
также
функция времени.
На базе ограничения
![]() получим некоторые ограничения на
получим некоторые ограничения на![]() .
.
Обозначим
![]() .
Мы знаем, что
.
Мы знаем, что![]() ,
таким образом
,
таким образом![]() .
Тогда само скалярное произведение
.
Тогда само скалярное произведение![]() - чисто мнимое число.
- чисто мнимое число.
Но
![]() - число вещественное. Отсюда можно
представить
- число вещественное. Отсюда можно
представить
![]() (19.1)
(19.1)
Здесь мнимая единица из соотношения
![]() .
Т. к. в (*) стоит линейный оператор
.
Т. к. в (*) стоит линейный оператор![]() ,
то это соотношение удовлетворяет
принципу суперпозиции.
,
то это соотношение удовлетворяет
принципу суперпозиции.
Подставим (19.1) в равенство
![]() ,
тогда
,
тогда
![]()
![]() - эта величина должна быть чисто
вещественной, тогда оператор
- эта величина должна быть чисто
вещественной, тогда оператор![]() - эрмитов:
- эрмитов:
![]() .
.
Свойства оператора
![]() :
:
В пределе перехода к классической
механике:
![]() ,
то
,
то![]() ,
гдеS – действие
из классической механики. Причем
,
гдеS – действие
из классической механики. Причем![]() ,
тогда рассматривая
,
тогда рассматривая
![]() ,
(19.2)
,
(19.2)
где
![]() -
функция Гамильтона.
-
функция Гамильтона.
В нашем случае
![]() ,
тогда учитывая предельный переход
,
тогда учитывая предельный переход![]() и (19.2), то:
и (19.2), то:
![]() .
.
Получили волновое уравнение:
![]()
![]() - нестационарное уравнение Шредингера
(волновое уравнение).
- нестационарное уравнение Шредингера
(волновое уравнение).
Каждой системе ставится в соответствие Гамильтониан, решаем с гамильтонианом уравнение Шредингера и получаем волновую функцию которая определяет эволюцию системы.
