Konspekt_lekcii Зандер

4.Построение модели по отклонениям уровней от среднего уровня. Справедливо в том случае, если уровни ряда колеблются около средней или имеют очень слабую тенденцию. В этом случае рассматриваемый метод равнозначен методу коррелирования отклонений от тренда. Если уровни ряда имеют ярко выраженную тенденцию, то метод неприемлем.

5.Введение времени в модель в качестве независимой переменной. Такая регрессионная модель, построенная методом коррелирования уровней с включением фактора времени, справедлива в том случае, если основные тенденции исследуемых рядов одинаковы. Если имеется запаздывание во влиянии факторных признаков на результативный, то это учитывается при моделировании независимо от того, каким методом строится модель.

81

Лекция 3.1.5. Циклические и сезонные колебания

Внутригодовые уровни многих показателей существенно зависят от сезонности. Так, например, расход электроэнергии в летние месяцы значительно меньше, чем в зимние. Производство многих видов продуктов (сахара, растительного масла и др.), связанных с переработкой сельскохозяйственной продукции, увеличивается в месяцы, следующие непосредственно за окончанием уборки урожая; цены на сезонную продукцию (овощи, фрукты и др.) неодинаковы в различные месяцы и т. д.

При графическом изображении таких рядов сезонные колебания наглядно проявляются в повышении или снижении уровней в определенные месяцы года. Причем попытки сгладить эти отклонения путем, например, укрупнения интервалов, приводят к затушевыванию тенденции. Обнаружить колеблемость в ряду, вызванную влиянием сезонности, возможно при наблюдении за месячными (квартальными) уровнями. Наблюдение за сезонными колебаниями представляет интерес с точки зрения стремления к их устранению, например, получить равномерную загрузку мощностей в сельском хозяйстве, строительстве, а также знание особенностей сезонных колебаний может быть использовано при решении многих практических задач, например, планирование выпуска продукции по месяцам, если спрос на нее подвержен влиянию сезонности, и соответственно, планирование потребности в рабочей силе, оборудовании и т.д. Поэтому изучение и измерение «сезонной» волны являются важными моментами при анализе рядов динамики.

Выравнивание при помощи ряда Фурье. Когда в эмпирическом ряду наблюдается периодичность изменения уровней, то представить эту периодичность уровней динамического ряда можно в виде гармонических колебаний, т. е. провести аналитическое выравнивание при помощи ряда

Фурье

n

X

ybt = a0 + (ak cos kt + bk sin kt):

k=1

Синусоиды, полученные при выравнивании рядом Фурье, называют

гармониками различных порядков. Показатель k в приведенном уравнении определяет число гармоник. Обычно при выравнивании по ряду

82

Фурье рассчитывают несколько гармоник (чаще не более четырех) и затем уже определяют, с каким числом гармоник наилучшим образом отражается периодичность изменения уровней ряда.

При выравнивании по ряду Фурье периодические колебания уровней динамического ряда как бы представляют в виде суммы нескольких синусоид (гармоник), наложенных друг на друга. Так, например, при k = 1 уравнение ряда Фурье будет выглядеть следующим образом:

ybt = a0 + a1 cos t + b1 sin t;

при k = 2, соответственно,

ybt = a0 + a1 cos t + b1 sin t + a2 cos t + b2 sin t и т. д.

Параметры уравнения теоретических уровней, определяемых рядом Фурье, находят, как и в других случаях, методом наименьших квадратов. В результате получены формулы для исчисления указанных выше параметров уравнения ряда Фурье:

Последовательные значения t обычно определяются от 0 с увеличе-

нием (приростом), равным 2 =n, где n — число уровней эмпирического ряда. Например, при n = 10 временные точки t можно записать следующим образом:

0; 5 ; 25 ; 35 ; 45 ; ; 65 ; 75 ; 85 ; 95 :

Выравнивание по ряду Фурье часто дает положительный эффект в рядах, содержащих сезонную волну. Обычно строятся модели первой гармоники, второй гармоники и т. д., а затем на основании показателей качества полученных уравнений выбирается наиболее близкая модель к фактическим уровням ряда.

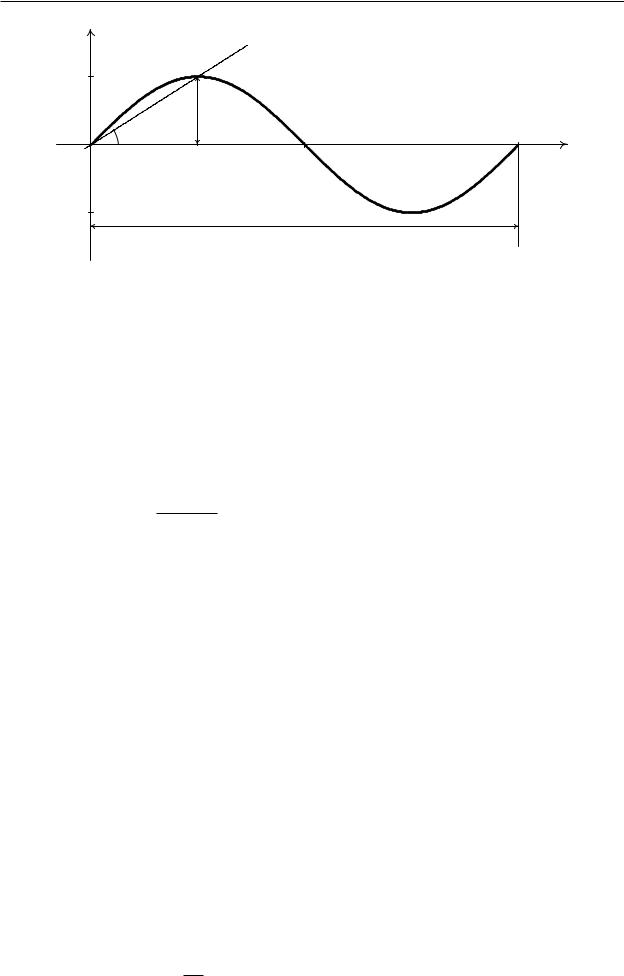
Рассмотрим модели временных рядов, где предполагается, что наблюдаемые временные ряды являются суммой периодического тренда и

83

1

Рис. 3.11

случайной компоненты, т. е.

yt = f (t) + "t;

причем детерминированная составляющая f (t) является периодической функцией и может описывать как циклические, так и сезонные колебания.

p

Здесь = 2 + 2, = arctg( = ).

Заметим, что период колебания временного ряда n может не сов-

падать с периодом колебания тригонометрического составляющего . Периодичность тренда означает, что он в точности повторяет себя

через определенный промежуток времени (т. е. f (t) = f (t + )), причем такое повторение абсолютно регулярно. Этот промежуток называют

периодом колебаний временного ряда ( ). Величина, обратная периоду, называется частотой (1= ). Она равна числу периодов (не обязательно целому), содержащемуся в единичном интервале. Иными словами, именно такое число раз функция повторяет свои значения.

Тригонометрические функции cos t и sin t являются периодическими с периодом 2 , т. е. cos (t+2 ) = cos t и sin (t+2 ) = sin t. Отсюда следует, что cos (t + 2 k) = cos t и sin (t + 2 k) = sin t, где k = 1; 2; : : : Можно преобразовать аргументы, сохранив при этом свойство периодичности. Функции cos ( t ) и sin ( t ) периодичны с периодом 2 = , т. е.

cos t + 2 = cos [ t + 2 ] = cos [ t ];

84

Умножение на соответствует растяжению или сжатию масштаба времени, а вычитание — сдвигу графика косинуса или синуса. Угол

называется фазой, причем обычно он выбирается так, чтобы периодическая функция косинуса достигала своего первого максимума в точке t = = . В таком случае 0 6 < 2 . При t = 0 указанные тригономет-

рические функции соответственно равны cos и ( sin ). Наибольшее

значение периодической функции называется амплитудой (обозначим его ).

Сдвинутые косинусоида и синусоида являются линейными комбинациями обычной косинусоиды и обычной синусоиды. Из тригонометри-

ческой формулы cos (a b) = cos a cos b + sin a sin b имеем

(cos t ) = [cos( t) cos + sin( t) sin ] = cos t + sin t;

Детерминированная составляющая модели временного ряда f (t)

может быть представлена суммой тригонометрических слагаемых общего

Здесь — период колебаний тригонометрического слагаемого, величина может не совпадать с периодом колебания временного ряда;

и — неизвестные параметры;

— амплитуда.

Пусть числовая последовательность y1; : : : ; yT имеет период n, где n — целое число, т. е. что

yt+n = yt; t = 1; : : : ; T n:

Представим T = nh, где T — число наблюдений, n — период колебаний временного ряда, h — число периодов в интервале наблюдений. Для полугодовых данных период равен 2, для ежеквартальных — 4, для

85

ежемесячных — 12. Наблюдаемые значения временного ряда можно точно аппроксимировать с помощью T линейно-независимых тригонометрических функций, причем максимальное число тригонометрических составляющих, входящих в разложение детерминированной составляющей модели временного ряда, определяется как:

быть и меньше qmax.

Порядок тригонометрического слагаемого 'k(t) задается числом k = 1; 2; : : : ; qmax, тогда тригонометрическое составляющее порядка k

(или гармонику порядка k) можно записать как

Период тригонометрического составляющего

nk = k :

Детерминированную составляющую периодических колебаний временного ряда можно представить в виде следующей суммы тригономет-

Представление называют разложением в ряд Фурье. Слагаемое

n=2( 1)t представляет собой периодическую функцию с периодом 2 . Оценки параметров для данной функции определяются с помощью

метода наименьших квадратов и минимизируют сумму квадратов отклонений фактических значений временного ряда от выравненных:

T

X

(yt ybt)2 ! min :

t=1

86

В результате решения системы уравнений независимые оценки параметров рассчитываются как:

Для временных рядов с четным n оценка

T

an=2 = T1 Xyt( 1)t:

t=1

Оценка дисперсии оценок параметров в модели сезонных колебаний вычисляется как

Представляет интерес проверка гипотезы об отсутствии циклического слагаемого с заданным наименьшим периодом, которая формулируется следующим образом

H0 : k = k = 0:

Если верна нулевая гипотеза, то величины k и k независимы и нормально распределены с нулевыми средними и дисперсиями 2 2=T . Тогда

статистика

T R2 F = k

4Sост2

имеет нормальное распределение с числом степеней свободы в числителе 1 = 2 и в знаменателе 2 = T p, где p — число оцениваемых коэффициентов.

87

Нулевая гипотеза отвергается с уровнем значимости , если критическое значение критерия Фишера (F ; 1; 2) превысит расчетное значение статистики F . Тогда делается вывод о том, что амплитуда колебаний тригонометрического слагаемого значимо отличается от нуля.

Проверка значимости параметров 0 и n=2 осуществляется с использованием статистики Стьюдента для уровня значимости и числа степеней свободы = T p. Расчетное значение t-статистики строится следующим образом:

Если tрасч больше tкрит, то принимается гипотеза о значимости параметров.

88

Тема 3.2. Системы линейных одновременных

уравнений

Лекция 3.2.1. Основные понятия.

Виды систем одновременных уравнений.

При изучении функционирования экономических систем исследователь обычно сталкивается со следующей ситуацией: состояние системы в каждый момент времени t описывается набором переменных, среди которых есть как эндогенные (внутрисистемные), так и экзогенные (внешние по отношению к рассматриваемой системе). Между переменными существуют функциональные и статистические связи. К первому типу относятся тождества, вытекающие из определений и содержательного смысла переменных. Ко второму типу относятся поведенческие связи, являющиеся выражением экономических законов, действующих в системе. Поскольку поведение экономических систем носит статистический характер (присутствуют случайные возмущения, погрешности, неучтенные факторы), то для описания поведенческих связей используются регрессионные уравнения. В теории экономико-статистического моделирования систему взаимосвязанных регрессионных уравнений и тождеств, в которой одни и те же переменные в различных регрессионных уравнениях могут одновременно выступать и в роли результирующих показателей, и в роли объясняющих переменных, принято называть системой одновременных (эконометрических) уравнений. При этом в соотношения могут входить переменные, относящиеся не только к периоду t, но и к предшествующим периодам, называемые лаговыми («запаздывающими») переменными.

Для экономистов большой интерес представляет количественный анализ модели, т. е. нахождение оценок параметров на основании имеющейся в распоряжении исследователя информации о значениях переменных. Первая из возникающих здесь проблем: можно ли в предложенной модели однозначно восстановить значение некоторого параметра или же его определение принципиально невозможно на основе рассматриваемой модели? Это так называемая проблема идентифицируемости.

89

Проблема оценивания здесь также имеет свои особенности. Основная трудность состоит здесь в том, что в эконометрических моделях переменная, играющая роль независимой (объясняющей) переменной в одном соотношении, может быть зависимой в другом. Это приводит к тому, что в регрессионных уравнениях системы объясняющие переменные и случайные возмущения оказываются коррелированными.

Рассмотрим в качестве иллюстрации два классических примера.

Пример 1. Модель спроса и предложения («крест Маршалла»).

Спрос Qd на некоторый продукт и его предложение Qs зависят от цены продукта p. Рыночный механизм формирует цену таким образом, что спрос и предложение уравниваются. Наблюдению доступна равновесная цена и спрос (совпадающий с предложением). Линейная модель

выглядит следующим образом:

Здесь pt — цена товара,

ut и "t — случайные возмущения, имеющие нулевые сред-

ние (t = 1; n).

Предполагается, что на рынке существует равновесие:

Qdt = Qst :

В соответствии с этой моделью цена и величина спросапредложения определяется одновременно, поэтому без дополнительных предположений (например, на структуру случайных возмущений) параметры i и i однозначно определить нельзя, т. е. они неидентифицируемы.

Пример 2.

Содержательный смысл модели спроса состоит в утверждении, что потребительские расходы, т. е. спрос, пропорциональны доходу. В свою очередь доход есть сумма потребительских и непотребительских расходов. Математическая формулировка модели такова:

ct = + yt + ut; yt = ct + zt;

90