Konspekt_lekcii Зандер

Если какой-либо уровень ряда превышает по своей величине каждый из предыдущих уровней, то величине ut присваивается значение 1, в остальных случаях она равна 0. Таким образом,

P

Суммирование проводят по всем членам ряда. Величины S и D

имеют независимые распределения и существенно зависят от порядка расположения уровней во времени. С помощью D проверяют, существует ли тенденция изменения в дисперсиях, а S позволяет обнаружить тенденцию в средней. С этой целью проверяются две гипотезы о том, существенно ли отличаются D от нуля и S — от (математического ожидания S). Эти гипотезы проверяются с помощью случайных величин

T1 и T2, где

T1 = D 0

2

и

S T2 = 1 ;

причем 2 и 1 — средние квадратические ошибки соответственно D и S. Величины T1 и T2 имеют распределение Стьюдента с числом степеней свободы, равным (n 1). Рассчитанные по формулам значения 1 и 2

сравнивают с табличными, найденными по таблицам критических точек распределения Стьюдента с уровнем значимости и числом степеней свободы (n 1).

Если T2 (расч) > tтабл, то принимается гипотеза о наличии тенденции в средней и говорят, что тренд существует. Если T1 (расч) > tтабл, то тенденция в дисперсии есть и описывается некоторым трендом. В противном случае говорят, что тенденция в дисперсии отсутствует.

61

Лекция 3.1.2. Сглаживающие процедуры.

Моделирование тенденции временного ряда

В случаях, когда тренд имеет незначительные колебания на довольно коротких интервалах времени, и невозможно представить его простой функцией времени на всем интервале, тогда используются статистические процедуры сглаживания (которые также называют фильтрованием).

Суть этих методов заключается в замене фактического значения ряда в данной точке на некоторую взвешенную среднюю величину значений, наблюдаемых в окрестности этой точки. При этом считается, что наблюдаемые значения являются суммой тренда и случайной ошибки. Грубо говоря, взвешенное среднее тренда совпадает со значением самого тренда в данной точке, а взвешенное среднее случайных составляющих имеет тенденцию становиться весьма малой величиной. Тем самым довольно нерегулярный график наблюдений заменяется гладким графиком скользящего среднего. Колеблемость ряда уменьшается, что позволяет оценить тренд взвешенной средней наблюдаемых значений. Расчетные значения определяются для всех точек ряда за исключением нескольких первых и последних.

Пусть имеются наблюдения y1; : : : ; yT . Тогда формула линейного фильтра (или сглаженного значения уровня в точке t) будет

Здесь yt является взвешенным средним наблюдаемых значений yt

в интервале значений временного параметра t, отстоящих от t не более чем на m единиц. Веса cs предполагаются нормированными, так что

m

X

cs = 1:

s= m

В случае, когда веса остаются постоянными (cs = const), то фильтры называют симметричными. Тогда результат сглаживания есть вариант среднего арифметического и сглаженное значение yt выражается

62

формулой

Вслучае, когда весовые коэффициенты не остаются постоянными,

т.е. когда, например, с приближением элемента ряда к уровню t его весовой коэффициент возрастает, то говорят о скользящей средней взвешенной. Если задается cs < cs+1, то фильтр позволяет учесть устаревание данных.

Существует и другая группа методов сглаживания, основанных на вычислении экспоненциальных средних значений уровня ряда по форму-

ле типа

m

X

yt = (1 cs)myt:

s= m

Однако методы сглаживания имеют ряд недостатков:

1.невозможно указать доверительные области и проверить гипотезы относительно тренда;

2.нельзя непосредственно связать построенную функцию с моделью образования тренда;

3.сглаженный ряд укорачивается по сравнению с фактическим, что приводит к не очень надежной экстраполяции тренда.

Всвязи с этим использование методов сглаживания больше применяется не для анализа ряда, а для его описания.

Моделирование тенденции временного ряда с помощью анали-

тического выравнивания

Наиболее распространенным и простым способом моделирования тенденции социально-экономического явления является аналитическое выравнивание временного ряда. Существуют различные приемы, но суть их одна — замена фактических уровней ряда расчетными, имеющими значительно меньшую колеблемость, чем исходные данные. Задача заключается в выборе наиболее подходящего типа кривой и оценке ее параметров.

63

Выбрать форму кривой можно, исходя из теоретического анализа сущности изучаемого явления и опираясь на опыт и знания самого исследователя.

Наибольшее распространение имеют линейные зависимости, т. е. функции типа

yt = a0 + a1t;

где yt — сглаженное (выравненное) значение уровня на момент t; коэффициенты a1; a2; : : : ; a — веса, приписываемые уровню ряда, находящемуся на расстоянии от момента t.

В зависимости от того, какие значения принимают весовые коэффициенты, сглаживание по данной формуле будет выполнено либо с помощью скользящих средних , либо экспоненциальных средних. Зависимости такого типа целесообразно применять для временных рядов с постоянным абсолютным приростом или снижением показателей (когда

уровни ряда увеличиваются в арифметической прогрессии).

Если анализируемая тенденция характеризуется постоянным темпом роста (рост уровней ряда идет в геометрической прогрессии), то

целесообразно проводить выравнивание по показательной функции:

yt = a0 + a1t или yt = a0ab11t+b2t2 :

При выравнивании временных рядов экономических явлений, характеризующихся стремлением к некоторой предельной величине, насыщением, используется модифицированная экспонента yt = a0 + a1at2.

Процессы с переменными темпами роста хорошо моделируются S- образными кривыми. К ним относятся логистические кривые и кривая Гомперца:

Для аппроксимации тренда часто используются полиномы различных степеней (как правило, до четвертой степени). Например, полином

первой степени yt = a0 + a1t, полином второй степени yt = a0 + a1t + a2t2, полином третьей степени yt = a0 + a1t + a2t2 + a3t3 и т. д.

64

Существуют различные приемы, позволяющие выбрать форму кривой, достаточно хорошо аппроксимирующей действительное развитие. Наиболее простой путь — визуальный, на основе графического изображения временного ряда. По виду графика подбирается уравнение кривой, которая ближе всего подходит к эмпирическому виду (траектории).

Другой путь выявления формы кривой заключается в применении метода последовательных разностей. Однако данный метод применяется только при подборе кривых, описываемых полиномами. Сущность этого метода заключается в нахождении первых, вторых и т. д. разностей

уровней, т. е.

1t = yt yt 1;2t = 1t 1t 1;

3t = 2t 2t 1и т. д.

Расчет этих разностей ведется до тех пор, пока разности не будут приблизительно равными. Порядок этих разностей и принимают за порядок искомого полинома.

При подборе функции тренда наряду с теоретическим анализом закономерностей развития явления используются и эмпирические методы. После того, как форма кривой будет выбрана, необходимо оценить параметры соответствующей модели. Если функция линейна, то для оценки тренда используется традиционная техника регрессионного анализа. В остальных случаях должны применяться приемы преобразования уровней (линеаризация) и нелинейный метод наименьших квадратов.

65

Лекция 3.1.3. Модели автокорреляции и авторегрессии

Среди моделей, отражающих свойства временных рядов, особо следует выделить модели автокорреляции и авторегрессии.

Автокорреляция — это корреляционная зависимость между последовательными (соседними) значениями уровней временного ряда y1 и y2, y2 и y3, y3 и y4 и т. д. Например, урожайность в определенные годы связана с урожайностью предшествующих лет, энерговооруженность производства за определенный год зависит каким-то образом от электровооруженности этого производства в предшествующие годы и т. д. Чтобы оценить степень зависимости между соседними уровнями временного ряда (автокорреляцию), рассчитывают коэффициенты автокорреляции между уровнями исходного ряда и того же ряда, но сдвинутого на шагов во времени. Величину называют шагом (или лагом).

Последовательность значений коэффициентов автокорреляции r , вычисленных при = 1; 2; : : : ; l, называют автокорреляционной функцией. Эта функция дает достаточно глубокое представление о внутренней структуре изучаемого экономического явления. Различают два типа автокорреляции, характерной для временных рядов: автокорреляцию уровней временного ряда yt, когда наблюдается зависимость уровней временного ряда, и автокорреляцию остаточной компоненты "t, когда ее значения зависят от предшествующих значений "t 1, "t 2 и т. д.

Коэффициенты автокорреляции рассчитываются по формуле парного коэффициента корреляции. Так, коэффициент автокорреляции первого порядка ( = 1) есть не что иное, как парный коэффициент корреляции между двумя рядами: y1; y2; : : : ; yT 1 и y2; y3; : : : ; yT 1; yT . Тогда

где y1 — средний уровень первого ряда; y2 — средний уровень второго ряда.

Аналогично вычисляются коэффициенты автокорреляции второго порядка = 2, третьего и т. д.

66

Общая формула для расчета коэффициента автокорреляции порядка запишется так:

При расчете коэффициентов автокорреляции с ростом порядка число коррелируемых пар уменьшается, а известно, что при небольшом числе наблюдений значимыми оказываются лишь высокие коэффициенты корреляции. Отсюда следует, что наибольшее значение должно быть таким, чтобы число пар наблюдений оказалось достаточным для вычисления коэффициентов автокорреляции r . В практике ориентируются на правило 6 T=4, где T — общее количество наблюдений временного ряда.

Коэффициент автокорреляции изменяется от 1 до 1. Близкое к нулю значение коэффициента говорит об отсутствии автокорреляции уровней ряда, а достаточно высокая по модулю величина свидетельствует об автокоррелированности ряда.

Если на оси абсцисс отложить значения , а на оси ординат — значения коэффициентов автокорреляции r , а затем точки с координатами ( ; r ) соединить отрезками прямой, то получится ломаная линия, которая называется коррелограммой. Анализ коррелограмм позволяет определить особенности стохастического процесса, отраженного в изучаемом ряду. Совокупность значений коэффициентов автокорреляции с разными лагами r1; r2; : : : ; rp образует корреляционную функцию.

Интерпретация коррелограмм требует определенного навыка и не всегда осуществима. Приведем несколько наиболее часто встречающихся ситуаций.

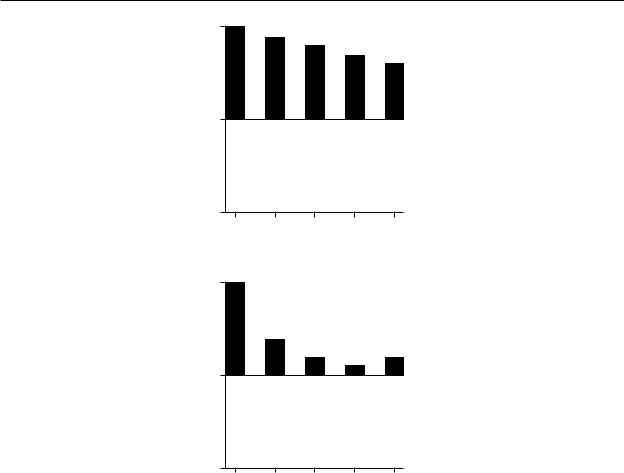
1.Если ряд содержит долгосрочную тенденцию к росту или к снижению, то все значения коэффициентов положительны, первый коэффициент r1 достаточно большой, а все последующие имеют тенденцию к снижению (рис. 3.1). Данный временной ряд хорошо аппроксимируется трендовыми моделями.

67

-1

1 2 3 4 5

Рис. 3.2

2.Если ряд имеет краткосрочные корреляции (зависимы смежные уровни ряда между собой), то первый коэффициент r1 положителен и имеет высокое значение (рис. 3.2). С увеличением временного лага корреляционная функция резко уменьшается и сохраняет лишь незначительные затухающие колебания около нуля. Для таких рядов целесообразно использовать авторегрессионные модели.

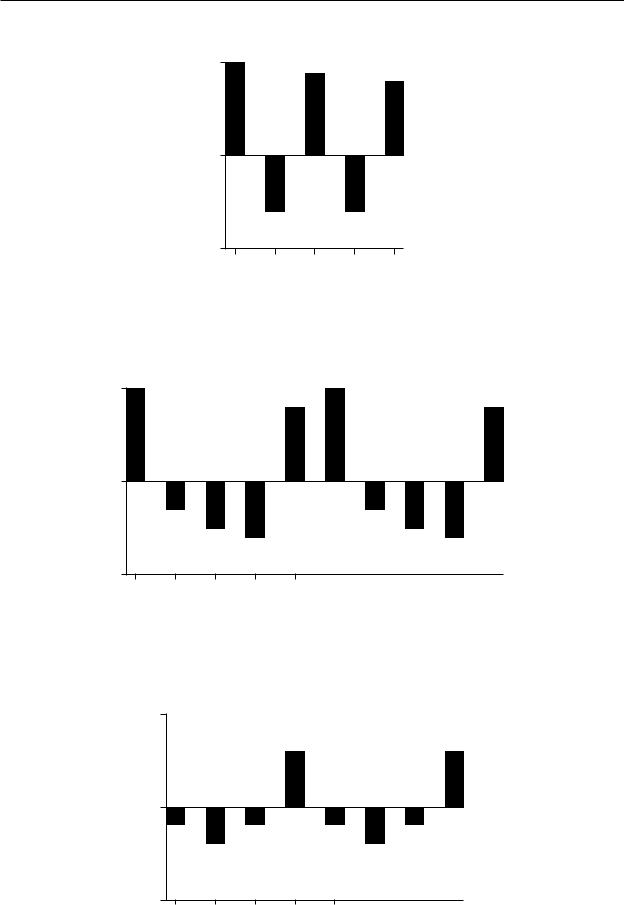
3.Если ряд имеет периодические колебания, то значения коэффициентов автокорреляции последовательно изменяют свой знак (рис. 3.3, 3.4, 3.5).

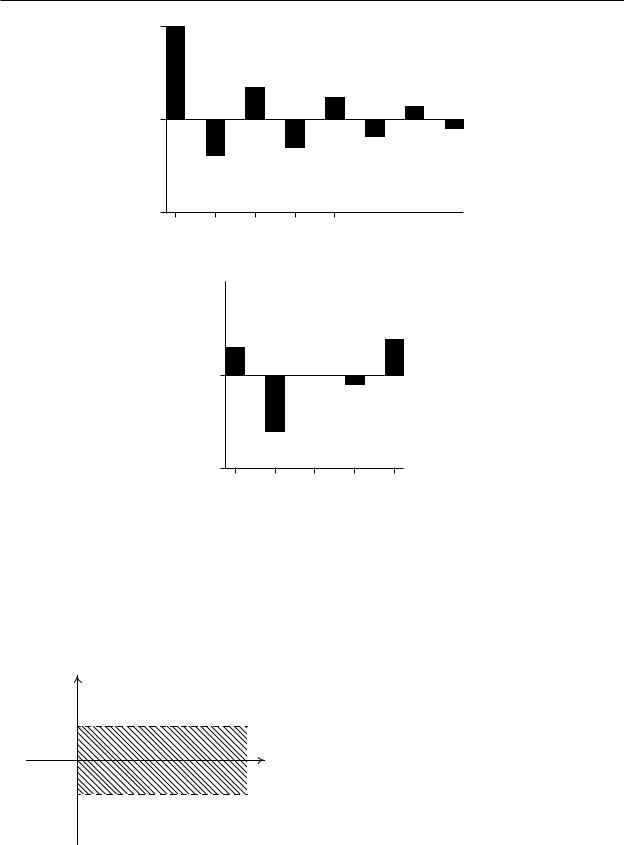
4.В случае стационарности временного ряда, когда с течением времени его математическое ожидание и дисперсия остаются постоянными, с ростом временного лага колебания коэффициентов автокорреляции затухают (рис. 3.6).

68

1 r

-1

1 2 3 4 5

Рис. 3.5

69

-1

-1

1 2 3 4 5

Рис. 3.7

5.Для полностью случайного ряда значения коэффициентов автокорреляции близки к нулю (рис. 3.7).

70