Задачи оптимизации

изводитель может приобрести на рынке ресурсов любой набор, состоящий из капитала K и труда L , который удовлетворяет равенству (3.1): C r K w L .

Бюджетной линией, или изокостой, назовем множество наборов факторов ( K, L ), имеющих одинаковую фиксированную стоимость C .

Изокоста допускает простую графическую интерпретацию. Если разрешить уравнение (3.1) относительно объема капитальных затрат K , то мы получим уравнение изокосты

соответственно.

Таким образом, уравнение изокосты полностью определяется тремя параметрами: бюджетным ограничением производителя C и стоимостями единицы капитальных и трудовых ресурсов r и w. Линия изокосты в выбранной системе координат имеет отрицательный наклон к оси абсцисс (см. рис. 7).

На рисунке 7 изображены две линии бюджетного ограничения для значений C 80 и С 60 (бюджетное ограничение выражено в условных единицах). Стоимость ресурсов производства для обеих кривых одинакова и равна: r 4 – стоимость капитальных ресурсов (в условных единицах) и w 20 – стоимость трудовых ресурсов (в условных единицах).

Рис. 7. Линии изокосты для бюджетных ограничений C 80 и С 60 . Значения стоимости ресурсов r 4 и w 20 одинаковы для обеих кривых

Из рисунка хорошо видно: при неизменной стоимости ресурсов производства линии бюджетных ограничений, соответствующие разным значениям C , образуют семейство параллельных линий.

Эффективное распределение ресурсов и равновесие производителя в долгосрочном периоде

Целью производителя является максимальное количество производимого продукта путем эффективного распределения ограниченных ресурсов.

Задачу об эффективном распределении ограниченных ресурсов будем решать, исходя из неоклассической экономической теории полагая, что производ-

2

ство описывается производственной функцией Y (K, L) с частичной заменой

факторов производства. Кроме того, будем предполагать, что в долгосрочном периоде производитель способен непрерывно изменять как величину затрачиваемого капитала, так и количество используемого труда.

Поскольку объем производства определяется производственной функцией Y (K, L) , которая предполагается известной, то максимальный объем производ-

ства при наличии ресурсного ограничения C r K w L может быть достигнут только за счет оптимального выбора величин K и L . Поэтому управление производством в долгосрочном периоде осуществляется путем наилучшего выбора набора потребляемых ресурсов K и L , когда цены ресурсов r и w рассматриваются как экзогенные (заданные извне) переменные.

С математической точки зрения задача о стационарном равновесии производителя в долгосрочном периоде требует нахождения набора факторов K, L ( K 0, L 0 ), который, с одной стороны, лежит на изокосте C r K w L , а с другой – реализует максимум функции Y (K, L) :

Поставленная выше задача (3.5) является частным случаем задачи нелинейного программирования и сводится к поиску условного экстремума функции многих переменных.

Для решения такого рода задач в математике используется метод неопределенных множителей Лагранжа. Сущность его состоит в том, что этот метод позволяет свести задачу на условный экстремум функции Y (K, L) к задаче на безусловный

экстремум функции L(K, L, ) , содержащей дополнительную переменную . Функцию L(K, L, ) определим таким образом, чтобы при выполнении условия C r K w L она не отличалась от функции Y (K, L) :

Необходимым условием экстремума функции (3.6) является равенство нулю частных производных от лагранжиана L(K, L, ) по независимым переменным

K, L, :

можно найти оптимальный набор факторов производства K, L . который обеспечивает максимальный выпуск продукции.

3

Дадим экономическую интерпретацию метода неопределенных множителей Лагранжа. Последнее из уравнений (3.7) просто обеспечивает выполнение бюджетного ограничения C r K w L , и поэтому эффективный набор факторов принадлежит изокосте. Экономический смысл первых двух уравнений легко

понятия предельного продукта, первые два уравнения запишем в виде системы равенств

Таким образом, для оптимального набора факторов справедливо равенство отношений предельного продукта фактора к цене фактора. Отношение предельного продукта фактора к цене единицы фактора ( MYK 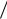r , например) пока-

зывает, какое количество дополнительной продукции будет произведено в случае вложения дополнительной платежной единицы при покупке фактора.

Смысл дополнительной переменной (неопределенного множителя Лагранжа) состоит в том, что он показывает, на сколько единиц продукции увеличится объем производства при вложении дополнительной платежной единицы на приобретение любого из факторов производства.

Из равенства (3.8) так же следует:

MYL w , MYK r

то есть для оптимального набора факторов предельная норма замещения одного фактора другим равна отношению цены первого фактора ко второму.

Можно дать простую геометрическую интерпретацию выбору оптимального набора факторов производства. Пусть бюджетное ограничение задано линией CD (см. рис. 8), а объем производства определяется

Рис. 8. Графическое определение эффективного распределения ресурсов

производственной функцией Y 2,248 K 0,404 L0,803 . Построим изокванту, соответствующую выпуску 8 единиц продукции (все величины измеряются в условных единицах). Видно, что изокванта пересекает изокосту в двух точках (А и В). Отсюда следует, что выпуск восьми единиц продукции при заданном бюджетном ограничении возможен при двух возможных сочетаниях факторов производства

4

( K, L ), задаваемых координатами точек пересечения изокванты и изокосты (точки А и В).

Видно, что выпуск восьми единиц продукции при заданном бюджетном ограничении не является оптимальным. Если увеличивать выпуск продукции, смещая изокванту, то точки пересечения изокванты и изокосты будут сближаться, пока не превратятся в одну единственную точку касания Р.

Дальнейшее увеличение объема производства становится невозможным, поскольку изокванта и изокоста не будут больше иметь общих точек. Таким образом, распределение ресурсов, определяемое точкой касания изокосты и изокванты, является оптимальным и определяет наибольший объем производства при заданном бюджетном ограничении и заданной стоимости факторов производства.

Пример 3.1

L0,75 , стоимость единицы капитальных и трудовых ресурсов одинаковы и равны: r 10 , w 10 (все величины измеряются в условных единицах). Производство имеет ресурсное ограничение C 80. Требуется определить, каким должно быть распределение ресурсов, обеспечивающее максимальный выпуск продукции.

Решение

Для решения задачи будем использовать метод неопределенных множителей Лагранжа. Учитывая данные задачи, составим систему уравнений для определения оптимального распределения ресурсов – аналог системы уравнений (3.7):

Поскольку правые части дух первых уравнений системы (3.9) равны, можно приравнять и их левые части

54 K 0,75 L0,75 154 K 0,25 L 0,25 .

Для дальнейшего упрощения этого уравнения левую и правую части его следует разделить на 5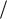4 и умножить на произведение K 0,25 L0,25 . В итоге полу-

чаем простое равенство L 3 K . Подставляя этот результат в последнее уравнение системы (3.9), находим K 2, L 6. Соответствующий объем производ-

ства равен Y * 5 20,25 60,75 22,795.

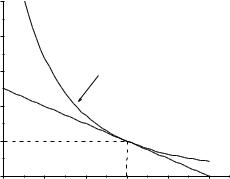
Графическое решение рассматриваемой задачи приведено на рис. 9. Оптимальные значения ресурсов K, L , обеспечивающие максимум производства, отмечены пунктирными линиями.

5

Рис. 9. Графическое решение задачи примера 3.1

После того, как найден оптимальный набор распределения ресурсов K 2, L 6, множитель Лагранжа можно найти либо из первого, либо из второго уравнения системы (3.9). В итоге имеем 0,285 . Смысл этой величины состоит в том, что если выбран оптимальный набор ресурсов производства, то вложение единицы платежных средств в покупку капитальных ресурсов и покупку трудовых ресурсов дает одинаковый прирост производства, равный 0,285 единиц.

Очевидно, что если бы прирост производства был разным, то имело бы смысл продать один ресурс (приводящий к меньшему уменьшению производства) и приобрести другой. То есть можно было бы улучшить набор факторов.

В принципе, используя метод неопределенных множителей Лагранжа, можно решить любую задачу нелинейного программирования, сводящуюся к системе уравнений (3.7).

Однако для решения практических задач этот метод может оказаться весьма трудоемким, поскольку требует решения системы нелинейных алгебраических уравнений. К счастью, в большинстве случаев можно ограничиться численным методом решения задачи оптимизации, используя надстройку электронных таблиц Excel Поиск решения. Подробнее мы будем обсуждать численные методы оптимизации в разделе, посвященном линейному программированию.

Как уже указывалось, возможна альтернативная постановка задачи, когда требуется при заданном объеме производства минимизировать затраты производителя. Математическая постановка такой задачи может выглядеть следующим образом:

Экзогенные величины r, w , как и раньше, имеют смысл стоимости единицы капитальных и трудовых ресурсов, Y0 – заданный объем производства.

6

Задачи (3.10) и (3.5) являются двойственными и приводят к одному и тому же оптимальному решению (при Y0 Y * ). Рассмотрим решение задачи (3.10) методом неопределенных множителей Лагранжа. Введем функцию Лагранжа

мальное распределение факторов производства, обеспечивающих заданный объем Y0 при минимизации полной стоимости затрат.

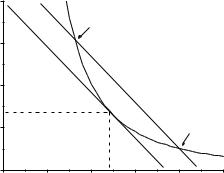
Графическое решение задачи (3.10) аналогично графическому методу решения задачи (3.5) (рис. 10). Единственное отличие состоит в том, что в этом случае фиксируется кривая изокванты с заданным объемом производства (на рис. 10 это линия изокванты, задающая объем производства Y0 22,795). Линия

изокосты может смещаться, оставаясь параллельной самой себе. Условие параллельности следует из того факта, что параметры r, w считаются экзогенными, т. е. неизменными в условиях задачи, а именно отношение этих параметров определяет тангенс угла наклона изокосты к оси абсцисс.

Рис. 10. Графическое решение задачи минимизации полной стоимости ресурсов производства при заданном объеме выпуска

Если изокоста не является оптимальной (линия CD на рис. 10), то возможны два различных набора факторов производства, определяемых точками А и В. Требуемый объем производства будет при этом достигнут, но стоимость набора ресурсов производства окажется выше оптимальной. Если смещать линию изокосты влево, то точки А и В будут сближаться, пока не сольются в одну единственную точку Р, где изокоста касается изокванты.

7

Таким образом, мы показали, что графическое решение двойственных задач оптимизации приводит к одинаковому оптимальному решению. Особенности графического решения двойственных задач представлены в табл. 3.1.

Таблица 3.1

Общая постановка задач оптимизации в экономике

Оптимизационная задача – это экономико-математическая задача нахождения оптимального (максимального или минимального) значения целевой функ-

В дальнейшем для сокращения записи введем векторные обозначения, пола-

гая X (x1, x2 , , xn ) .

Для того чтобы решить задачу оптимизации, достаточно найти ее оптимально решение, т. е. указать такой вектор значений X0 W (в экономике это реше-

ние часто называют оптимальным планом), для которого выполняется условие f (X0 ) f (X ) для всех X W . Задача поиска минимума сводится к задаче (3.13) поиска максимума функции простой сменой знака целевой функции f (x1, x2 , , xn ) .

Оптимизационная задача является неразрешимой, если она не имеет оптимального решения на допустимой области значений функции.

Методы решения оптимизационных задач зависят как от вида целевой функции f ( X ) , так и от строения допустимого множества значений аргументов це-

левой функции W (в экономике это множество также называют множеством допустимых планов).

Математическим программированием называется раздел математики,

посвященный теории и методам поиска экстремума в задачах вида (3.13), для которых вектор X принадлежит конечномерному векторному пространству, а область ограничений W определяется системой равенств или неравенств.

В свою очередь, в математическом программировании в зависимости от вида целевой функции f ( X ) и вида области ограничения W принято выделять задачи:

линейного программирования;

нелинейного программирования;

целочисленного программирования;

стохастического программирования;

динамического программирования.

8

В дальнейшем при изложении материала этой темы мы рассмотрим различные постановки и примеры решения задач математического программирования.

Задачи линейного программирования

Для задач этого класса предполагается, что целевая функция и все ограничения линейны. Таким образом, задача линейного программирования может быть записана следующим образом:

Первое уравнение системы (3.14) представляет собой линейную целевую функцию, минимум которой требуется найти, предполагая, что коэффициенты ci являются известными, заданными величинами.

Второе и третье уравнения определяют допустимое множество решений. Коэф-

ными величинами. Допустимое множество решений может оказаться пустым. Тогда поставленная выше задача линейного программирования решения не имеет. Пустое множество допустимых решений может получиться в том случае, когда число уравнений, задающих ограничения, превышает число переменных задачи, т. е. когда m n .

Оптимальным решением, или оптимальным планом, называется век-

тор X (x1, x2 , , xn ) , который удовлетворяет системе ограничений и реализует

минимум целевой функции.

Система уравнений (3.14) реализует так называемую общую постановку задачи линейного программирования.

Всякая задача линейного программирования может быть приведена к канонической форме записи

Сравнивая постановки задач линейного программирования (3.14) и (3.15), легко сформулировать правила перехода к канонической записи:

9

если в исходной записи требуется определить максимум целевой функции, то следует сменить знак целевой функции и искать минимум;

если в уравнении ограничения правая часть отрицательна, то следует умножить левую и правую части уравнения, задающего ограничение, на 1;

если среди ограничений имеются неравенства, то они путем введения новых неотрицательных переменных преобразуются в равенства. При этом в каждое неравенство достаточно добавить одну новую переменную.

Впринципе, может встретиться случай, когда одна или несколько переменных xk могут принимать только отрицательные значения. В этом случае следует вве-

функции, так и в уравнениях ограничений.

Пример 3.2

Следующую задачу линейного программирования привести к канонической форме

Решение

Поскольку переменная x1 определена на отрицательной полуоси, введем но-

вую переменную x1 x1 0 . В задаче требуется найти максимум целевой

функции. Поэтому поменяем знак у целевой функции, и будем искать минимум этой новой функции. В итоге первое из уравнений (3.16) запишется в виде

2 x1 x2 x3 min .

Во втором уравнении добавим новую положительно определенную переменную x4 и запишем уравнение в виде 2 x2 x3 x4 5.

В третьем уравнении отрицательна правая часть. Поэтому сначала умножим левую и правую части уравнения на 1, произведем замену x1 x1 и добавим

переменную x5 . В итоге третье уравнение запишется в виде x1 x2 x3 x5 1.

Аналогично производится и преобразование четвертого уравнения системы

(3.16).

Собирая все результаты вместе, получаем каноническую запись задачи линейного программирования (3.16):

10