
Задачи оптимизации
.pdf
1 3, |
2 5,5, |
3 4 . Выбирая максимальное из этих значений, снова прихо- |
дим к заключению, что оптимальной является вторая стратегия.
Подводя итоги, еще раз заметим, что единого подхода к решению задач в условиях неопределенности не существует. Выбор решения остается за ЛПР и зависит от его склонности к риску. Тем не менее все испробованные выше стратегии принятия решения в условиях полной неопределенности привели нас к заключению, что оптимальной при данной матрице платежей является вторая стратегия игрока.
Принятие решений в условиях риска
Если состояниям природы можно поставить в соответствие вероятности их реализации, найденные статистическим путем или с помощью экспертного заключения, то решение обычно принимается на основании максимума ожидаемого среднего выигрыша или минимума ожидаемого среднего риска. Иначе говоря, если для некоторой игры с природой задана платежная матрица aij , а
стратегиям природы j , j 1, |
2, |
, n , сопоставлены вероятности |
p j , то при- |
нимается стратегия игрока Ai , |
i 1, |
2, , m , для которой |
|
|
|
n |
|
|
|
aij p j max . |
(3.33) |
|
|
j 1 |
|
Если для построения критерия используется матрица рисков (матрица упущенных выгод) rij , то лучшей будет та стратегия, которая обеспечивает мини-
мальный средний риск:
n |
|
rij p j min . |
(3.34) |
j 1
Критерии, основанные на использовании ожидаемого значения выигрыша (3.33) или ожидаемого риска (3.34), целесообразно использовать, когда одно и то же решение приходится применять достаточно большое число раз.
Если решение приходится принимать однократно, то критерии (3.33), (3.34) могут привести к ошибочным результатам. В этом случае необходимо использовать один из вариантов многокритериальной оптимизации, выбирая стратегию, приводящую к максимуму ожидаемого выигрыша и минимальному значению его дисперсии. Например, можно предложить следующий критерий выбора:
M(X ) k (X ) max . |
(3.35) |
В формуле (3.35) M( X ) – математическое ожидание некоторой случайной величины X (например, прибыли предприятия), ( X ) – среднеквадратическое
отклонение этой случайной величины, k – некоторый положительный числовой коэффициент, который учитывает склонность ЛПР к риску при принятии решения. Например, предприниматель, очень остро реагирующий на большие колебания прибыли, выберет k достаточно большим, обеспечив выбор стратегии, приводящей к меньшим возможным колебаниям выигрыша.
51

Пример 3.15
Для доставки свежих фруктов из Кишинева в Москву можно использовать три вида транспорта: A1 – воздушный, A2 – автомобильный, A3 – железнодо-
рожный. Менеджер транспортной компании принял, что на каждом из видов транспорта могут сложиться три ситуации: – благоприятная, нейтральная и неблагоприятная – и рассчитал для этих ситуаций ожидаемый доход компании (млн руб.). Вероятности реализации благоприятной, нейтральной и неблагоприятной ситуаций на разных видах транспорта, которые менеджер получил на основании данных работы компании за прошлые годы, оказались различными. В таблице ниже приведены данные ожидаемой прибыли и веро-
ятности реализации различных состояний транспортной системы
1, 2 , 3 .
Вид транспорта |
|
1 |
2 |
3 |
|
|
|
|
|
|
|
Воздушный |
P |
0,6 |
0,39 |
0,01 |
|
1 |
|
|
|
||
|
A1 |
600 |
300 |
300 |
|
|
|
|
|
|
|
Автомобильный |
P2 |
0,2 |
0,79 |
0,01 |
|
A2 |
450 |
300 |
200 |
||
|
|||||
|
|
|
|
|
|
Железнодорожный |
P3 |
0,19 |
0,8 |
0,01 |
|
A3 |
600 |
450 |
100 |
||
|
Какой вид транспорта следует выбрать для доставки фруктов?
Решение
Для принятия решения будем использовать критерий (3.35), полагая значение коэффициента k 3 . Смысл такого выбора состоит в том, что если случайная величина подчиняется нормальному распределению, то с вероятно-
стью 0,997 значения этой случайной величины находятся в интервале
Μ(X ) 3 X M(x) 3 .
Используя в качестве критерия условие максимума величины M(X ) 3 ( X ) , мы по существу выбираем стратегию с самым большим ми-
нимальным выигрышем.
Найдем средние значения M( X ) , среднеквадратические отклонения для
всех трех вариантов перевозки. Для удобства эти данные сведены в таблицу, приведенную ниже.
Вид транспорта |
M( X ) |
|
M( X ) 3 |
M( X ) 3 |
|
|
|
|
|
Воздушный |
474 |
165,29 |
– 21,90 |
969,90 |
Автомобильный |
325 |
79,84 |
85,47 |
564,53 |
Железнодорожный |
473 |
82,28 |
226,14 |
719,86 |
|
|
|
|
|
Проанализируем представленные в таблице результаты. Ожидаемое значение прибыли оказалось практически одинаковым для перевозки фруктов воз-
52
душным и железнодорожным транспортом, но минимально возможная прибыль существенно выше в случае железнодорожных перевозок. Поэтому при принятии решения следует выбрать стратегию перевозки фруктов железной дорогой.
Максимально возможная прибыль выше при перевозке фруктов авиатранспортом. Если менеджер склонен к риску и использует принцип «либо пан, либо пропал», то он может ратовать за использование воздушного транспорта.
В связи с рассмотренной задачей остановимся также на проблеме оценки стоимости информации. Представим себе, что чиновник, контролирующий железнодорожные перевозки, обещает обеспечить самые благоприятные условия перевозки (или знает, что условия самые благоприятные), но за эту услугу (информацию) требует определенную плату. Какова верхняя оценка стоимости такой услуги (информации)?
Очевидно, что в качестве верхней оценки стоимости этой услуги можно взять разность прибыли в условиях полной определенности, когда стратегия однозначно выбрана, и средней статистической прибыли. В условиях точного знания, что перевозки железнодорожным транспортом будут проходить в самых оптимальных условиях, прибыль составит 600 млн руб., а среднестатистическая прибыль – 473 млн руб. Поэтому в качестве верхней оценки стоимости информации о том, что условия перевозки по железной дороге являются наилучшими является разность 600 – 473 = 127 (млн руб.).
Выбор решений с помощью дерева решений
Рассмотрим кратко более сложные (позиционные или многоэтапные) решения в условиях риска. В этом случае решения формируются в результате многоэтапной процедуры, когда на каждом шаге могут быть свои состояния природы и вероятности их реализации. Решение, принятое на каждом предыдущем шаге, влияет на последующее решение.
Таким образом, можно сказать, что если имеются два или более последовательных этапов принятия решения, причем последующие решения основываются на предыдущих, и два или более состояний среды, то в этих условиях для принятия решения используется дерево решений.
Дерево решений – это графическое изображение последовательности решений и состояний среды с указание соответствующих вероятностей и выигрышей для любых комбинаций стратегий и состояний среды.
Следует понимать, что дерево решений – это лишь способ наглядно отобразить существующие стратегии, вероятности состояния природы и выигрыши, соответствующие различным альтернативам. Использование дерева решений существенно упрощается, если использовать надстройку Excel TreePlan.xla. Эта надстройка позволяет автоматизировать расчет выигрыша по заданным вероятностям и матрице платежей.
53

Применение надстройки будет продемонстрировано на практических занятиях. Рассмотрим лишь один пример принятия решений с использованием дерева решений и продемонстрируем схему применения этого метода.
Пример 3.16
Руководство компании решает, создавать ли для выпуска новой продукции новое крупное производство, ограничиться ли строительством малого предприятия или продать патент другой фирме. Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка
|
Состояние рынка и вероятности |
|
|||
Стратегия компании |
реализации этого состояния p |
|
|||
|
|
|
|
|
|
|
Благоприятное |
p |
Неблагоприятное |
p |
|
|
|
|
|
|
|
Строительство крупного |
200000 |
0,6 |
–180000 |
0,4 |
|
предприятия (А) |
|||||
|
|
|
|
||
|
|
|
|
|
|
Строительство малого |
100000 |
0,8 |
-20000 |
0,2 |
|
предприятия (Б) |
|||||
|
|
|
|
||
|
|
|
|
|
|
Продажа патента (С) |
28000 |
0,7 |
15000 |
0,3 |
|
|
|
|
|
|
|
Какое решение следует принять компании?
Решение
На рис. 26 изображено дерево решений для рассматриваемой задачи. С помощью надстройки Excel TreePlan.xla это дерево строится практически автоматически, нужно лишь ввести значения выигрышей для различных состояний природы и вероятности этих состояний.
Рис. 26. Дерево решений для задачи примера 3.16
54

Цифры, которые записаны возле каждой из вершин дерева (на диаграмме они изображены кружками), представляют собой ожидаемый выигрыш для этой вершины. Таким образом, в рассмотренном примере следует выбрать стратегию Б, которая дает наибольший выигрыш.
Функция полезности Неймана – Моргенштерна
До сих пор предполагалось, что решения принимаются с позиции «объективиста». Это означает что ЛПР, будучи трезвомыслящим человеком, откажется от игры, если ему предложат взамен сумму, равную среднестатистическому выигрышу (ожидаемую денежную оценку игры).
Вдействительности ЛПР может оказаться «субъективистом» и быть либо чрезмерно осторожным, либо склонным к рискованным решениям.
Влюбом случае ЛПР принимает решение, стремясь максимизировать ожидаемую полезность. Таким образом, полезность наряду с матрицей платежей или матрицей рисков – это еще один способ измерить привлекательность принимаемых решений.
Полезность – это некоторое число, которое можно сопоставить каждому возможному исходу. Каждое лицо, принимающее решения, имеет свою функцию полезности, которая показывает его предпочтения к тем или иным исходам
взависимости от величины риска. Таким образом, функция полезности будет выглядеть по-разному для людей избегающих риск и людей склонных к риску
(рис. 27).
1,4 |
U(x) |
|
|
B |
|
|
|
|
|
|
|
1,2 |
|
|
|
|
|
|
c1 |
|
|
|
A |
1,0 |
|
|
|
|
|
0,8 |
b1 |
|
|
|
|
0,6 |
a1 |
|
c |
|
|
a |
b |
|
|
||
|
|
|
|||
|
|
|
|
||
0,4 |
|
|
|
|
|
0,2 |
|
|
|
|
x |
|
|
|
|
|
|
0 |
400 |
|
800 |
1200 |
1600 |
Рис.27. Функция полезности для лиц, избегающих риска (кривая А), и лиц, склонных к риску (кривая В)
Пусть человеку, имеющему, например, 600 рублей, предлагают сыграть в лотерею, в которой он с вероятностью 50% может выиграть 200 рублей и с вероятностью 50 % проиграть 200 рублей. Очевидно, что человек, не склонный к риску, отклонит это предложение, поскольку если он выиграет, то функция полезности увеличится на величину c1b1 , а если проиграет, то уменьшится на ве-
личину b1a1 .
Иначе говоря, ущерб от потери 200 рублей для такого человека существенно больше, нежели удовлетворение от получения 200 рублей (относительная полезность денег убывает и описывается выпуклой вверх функцией полезности).
Для человека, склонному к риску, наоборот, возможность выигрыша 200 рублей является решающим фактором. Функция полезности в этом случае яв-
55
ляется выпуклой вниз, и относительная полезность денег растет при их увеличении (кривая В).
Функцию полезности в теорию принятия решений впервые стали использовать американские ученые Дж. Нейман и О. Моргенштерн.
Естественно встает вопрос о том, как можно определить явный вид этой функции для того или иного ЛПР? Существует несколько способов определения функции полезности. Мы рассмотрим самый простой, когда известна функциональная зависимость U (x) , где U – функция полезности, x – выигрыш. В этом случае ин-
дивидуальным является лишь один параметр, который и определяется по склонности ЛПР к риску.
Чаще других за основу берется экспоненциальная функция. Например, при анализе решений, связанных с инвестициями, и во многих других бизнесприложениях используется функция полезности
U (x) 1 e x/r . |
(3.36) |
В этой формуле x – денежная сумма, которой мы должны приписать определенное значение полезности, r – определяет меру предрасположенности к риску. График этой функции при значении параметра r 300 изображен на рис. 27 (кривая А). Чем больше значение r , тем более компания или индивидуум склонны к риску.
Есть несколько простых способов определить величину r . В первом из них ЛПР предлагают либо сыграть в игру, в которой он может с вероятностью 50 % выиграть r рублей или с той же вероятностью потерять r 2 рублей, либо отка-
2 рублей, либо отка-
заться от игры вообще и «остаться при своих». Эмпирически найденная величина r , при которой ЛПР откажется от игры и будет мерилом склонности к риску в функции полезности(3.36).
Другой способ основан на экспертной оценке. По данным американской литературы оценка величины r для компании составляет либо 124% величины чистой прибыли, либо 15,7% объема капитала, либо 6,4% объема чистых продаж.
Если событие может иметь несколько исходов, то ожидаемая полезность события равна сумме произведений вероятностей исходов на значение их полезности.
Пример 3.17
Бизнесмен имеет функцию полезности U (x) 10 2 x , где x – денежный
выигрыш (тыс. долларов). Он может вложить 25 тыс. долларов в строительство бара и гриля. С вероятностью 0,5 он потеряет весь свой капитал и с той же вероятностью выиграет 32 тыс. долларов.
Будет ли менеджер инвестировать свой капитал?
Решение
Если не инвестировать капитал (x 0) , то значение функции полезности будет равно U (0) 10 2 0 10. Если инвестировать, то с вероятностью 0,5
x 25 , |
и |
функция |
полезности |
для |
этого |
исхода |
равна |
56

U ( 25) 10 2 25 40 . С вероятностью 0,5 выигрыш составит 32 тыс. долларов, а функция полезности для этого исхода равна U (32) 10 2 32 74 .
Таким образом, ожидаемая полезность при инвестировании составит
U 0,5 (U ( 25) U (32)) 0,5 ( 40 74) 17 . Поскольку полезность инве-
стирования оказалась выше, бизнесмен будет вкладывать капитал в строительство бара и гриля.
Оптимизация портфеля ценных бумаг
Постановка задачи
Рассмотрим общую постановку задачи распределения капитала, который участник рынка хочет потратить на покупку ценных бумаг. Эта задача, являясь важной в практическом отношении, как нельзя лучше демонстрирует применение игровых и оптимизационных методов в принятии важных экономических и управленческих решений.
Набор ценных бумаг, находящихся у участника рынка, называется его портфелем. Стоимость портфеля P – это стоимость всех его ценных бумаг. Доходностью портфеля d обычно называют удельный прирост его стоимости за год: d (P P) P , где P – стоимость портфеля через год. Очевидно, что
P , где P – стоимость портфеля через год. Очевидно, что
если di – доходность i го актива портфеля, а xi – доля этого актива в портфеле, то доходность портфеля будет определяться формулой
n |
|
d xidi , |
(3.37) |
i 1
где n – число различных видов активов в портфеле.
Как правило, доходность ценных бумаг колеблется во времени, так что ее можно считать случайной величиной. Если наблюдение за активами ведется достаточно давно (например, на протяжении k временных интервалов), то мож-
|
|
|
|
|
, дисперсию 2 |
|
|||||
но вычислить среднюю доходность актива d |
или среднеквад- |
||||||||||
|
|
|
|
|
|
i |
|
|
i |
|
|
ратическое отклонение актива i : |
|
|
|
|
|
|
|
|
|||
|
|
1 |
k |
|
1 |
|
k |
|
|||
|
|
di s , |
i2 |
|
|
|
|
|
|||
|
di |
|
(di s di )2 . |
(3.38) |
|||||||
|
k |
k |
|||||||||
|
|
s 1 |
|
s 1 |
|
||||||
Суммирование по s |
здесь производится по годам наблюдения. Среднеквад- |
||||||||||
ратическое отклонение |
доходности |
актива |
|
i можно интерпретировать как |
|||||||
риск данного актива.
Так как доходность составляющих портфель ценных бумаг случайна, то случайной будет и доходность портфеля. Определим математическое ожидание
доходности d , дисперсию 2 (риск) портфеля ценных бумаг:
57

|
|
|
n |
|
|
|
|
1 |
n |
n |
k |
|
|
|
|
|
|||||
d |
xi di , |
|
2 |
(di s di ) (d j s d j ) xi x j |
|
||||||||||||||||
k |
|
||||||||||||||||||||
|
|
|
i 1 |
|
|
i 1 |
j 1 |
s 1 |
(3.39) |
||||||||||||
|
|
n |
n |
|
|
|
|
1 |
k |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Vij xi x j , |
|
|
|
|
|
|
|
|
|||||||||||||
Vij |
(di s di ) (d j s d j ) |
|
|||||||||||||||||||
k |
|
||||||||||||||||||||
|
|
i 1 |
j 1 |
|
|
|
|
s 1 |
|
|
|
|
|
|
|
|
|
|
|||
где Vij – ковариационная матрица активов.
Модель Марковица
Суммируя приведенные выше результаты, легко сформулировать основные результаты портфельной теории Г. Марковица, которые были получены им еще в 1950 г. В 1990 г. за эту работу Г. Марковиц был удостоен Нобелевской премии по экономике.
Очевидно, что любой инвестор, вкладывая свои средства, желает сделать максимальным доходность портфеля ценных бумаг и минимальным его риск. Следовательно, мы приходим к оптимизационной задаче
n |
n n |
n |
|
||
|
|
|
Vij xi x j min, xi 1. |
|
|
xi di max, |
(3.40) |
||||
i 1 |
i 1 j 1 |
i 1 |
|
||
Если инвестор только вкладывает деньги и не участвует в операциях коротких продаж, то все величины xi 0, i 1, 2, , n .
Поставленная оптимизационная задача является двухкритериальной. Как мы уже знаем, не существует строгих алгоритмов решения задач многокритериальной оптимизации. По этой причине задача (3.40) сводится к однокритериальной, заданием некоторого приемлемого уровня доходности (первый из критериев (3.40) заменяется ограничением). Полученная таким образом задача
|
n |
n |
i |
|
j |
|
n |
|
|
i |
|
|
|
n |
|
|
2 |
ij |
|
|
i |
|
|
|
|
|
i |
|
|
||||
|
|
x |
x |
|
min, |
|
|
|
|
|
|
|
|
1, |
|
|
|
V |
|
x |
d |
|
d |
, |
x |
(3.41) |
|||||||
|
i 1 j 1 |
|
|
|
|
i 1 |
|
|
|
|
|
|
i 1 |
|
|
|
известна в литературе как однокритериальная задача оптимизации инвестиционного портфеля Г. Марковица.
Если задавать некоторое значение доходности портфеля d и, решая оптими-
зационную задачу (3.41), вычислять значение риска 2 , то мы получим множество пар точек, которые, если их построить в координатных осях «доходность – риск портфеля», образуют замкнутую кривую, изображенную схематически на рис. 28.
58

Риск
0,05 |
|
|
|
|
|
|
|
0,04 |
|
С |
|
С |
2 |
|
|
|
|
|
|
|
|
||
0,03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
0,02 |
|
|
|
|
|
|
|
0,01 |
|
С |
|
|
С |
3 |
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
0,00 |
|
|
|
|
|
|
|
0 |
2 |
|
4 |
6 |
8 |
10 |
|
|
|
|
|
|
Доходность |
||
Рис.28. Парето-оптимальные, или эффективные, портфели
Поскольку портфели оцениваются по двум характеристикам – доходности и риску, то между ними можно установить отношения доминирования.
Очевидно, что портфель С на рис. 28 является менее эффективным чем портфели C1 (у портфеля C1 меньше риск при той же доходности), C2 (у портфеля
C2 больше доход при том же риске) и C3 (у этого портфеля больше доход и
меньше риск, нежели у портфеля С).
Таким образом, легко показать, что доминирующими будут портфели, принадлежащие дуге АВ. В теории многокритериальной оптимизации портфели, которые не могут быть улучшены сразу по двум показателям – доходности и риску, называются Парето-оптимальными, или эффективными.
Какой из эффективных портфелей выбрать, решает ЛПР, и его решение зависит уже от индивидуальной склонности к риску.
Завершая раздел, посвященный модели Марковица, приведем расчетные формулы для случаев, когда портфель состоит из двух и из трех активов. Для случая, когда портфель состоит всего из двух ценных бумаг, математическая модель (3.41) может быть записана в форме
2 |
x2 |
2 V |
x |
x |
2 x2 |
min; |
||||||||||||
1 |
1 |
12 |
1 |
2 |
2 |
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x1 d1 x2 d2 d ; |
|
|
|
|
|
|||||||||||||
x1 x2 |
1; |
|
|
|
|
|
|
|
|
(3.42) |
||||||||
|
|
1 |
k |
|
|
|
|
|
|
|
|
|
|
|||||
V12 |
(d1 s d1) (d2 s d2 ). |
|||||||||||||||||
k |
||||||||||||||||||
|
|
|
|
s 1 |
|
|
|
|
|
|
|
|
|
|
||||
где k , как и раньше, число периодов наблюдения за доходностью активов.
Для портфеля, содержащего три вида ценных бумаг, оптимизационная модель несколько усложнится:
59
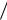
2 |
x2 |
2 |
x2 |
2 |
x2 |
2 V |
x |
x |
2 V |
x |
x |
2 V |
x |
x |
min; |
||||||||||
1 |
1 |
2 |
2 |
3 |
3 |
12 |
1 |
2 |
13 |
1 |
3 |
23 |
2 |
3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x1 d1 x2 d2 x3 d3 d ; |
|
|
|
|
|
|
|
|
|
||||||||||||||||
x1 x2 |
x3 |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ест |
||||
|
|
1 |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vij |
(di s di ) (d j s d j ); |
i, j 1, 2, 3. |
|
|
|
|
|
(3.43) |
|||||||||||||||||
k |
|
|
|
|
|
||||||||||||||||||||
|
|
|
s 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ественно, что инвестор может выдвинуть дополнительные требования при формировании портфеля ценных бумаг, которые нетрудно учесть, дополняя ограничения модели.
Модель Шарпа
Пусть в портфеле собрано n различных видов ценных бумаг. Разложим дисперсию портфеля на две группы:
n |
n |
|
2 xi2 |
Vii xi x j Vij . |
(3.44) |
i 1 |
i j |
|
В первой сумме правой части выражения (3.44) число слагаемых равно n , а во второй – n(n 1) . Предположим теперь, что доля каждого из активов в порт-
феле одинакова и xi 1 n , а доходности различных активов некоррелированы, т. е Vij 0, если i j . Тогда формула для дисперсии портфеля (3.44) может быть записана в виде
n , а доходности различных активов некоррелированы, т. е Vij 0, если i j . Тогда формула для дисперсии портфеля (3.44) может быть записана в виде
|
1 |
n |
|
|
2 |
Vii n . |
(3.45) |
||
|
||||
|
n i 1 |
|
||
Очевидно, что величина (3.45) с ростом n стремится к нулю. В этом и состоит эффект диверсификации портфеля.
Как показали исследования западных ученых, портфель, состоящий из хорошо подобранных 10 – 20 активов, способен фактически полностью исключить нерыночный риск.
В реальности все ценные бумаги обращаются на рынке, испытывая воздействие общеэкономических факторов. Поэтому имеется корреляция активов портфеля и рынка. Эта корреляция определяет рыночный, или систематический, риск портфеля.
Его нельзя исключить, потому что это риск всей системы. Широко диверсифицированный портфель заключает в себе практически только рыночный риск. Слабо диверсифицированный портфель обладает как рыночным, так и нерыночным риском. Таким образом, инвестор может снизить свой риск только до уровня рыночного, если сформирует широко диверсифицированный портфель.
Для измерения рыночного риска актива (портфеля) используется специальный коэффициент , который показывает зависимость между доходностью актива (портфеля) и доходностью рынка. Доходность рынка – это доходность рыночного портфеля. Поскольку невозможно сформировать портфель, в который бы входили все финансовые активы, то в качестве него принимается какой-либо индекс с широкой базой. Поэтому доходность рынка – это доходность портфе-
60
