Задачи оптимизации

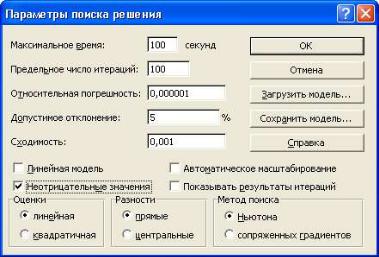
Значения нормированного градиента в отчете по устойчивости для нелинейных моделей интерпретируется аналогично значениям нормированной стоимости в отчете по устойчивости для линейных моделей. Если результирующее значение переменной положительно, то нормированный градиент будет равен нулю. Если результирующее значение переменной равно нулю, то нормированный градиент окажется отличным от нуля. В этом случае его можно интерпретировать как теневую цену дополнительного ограничения, которое следует ввести, чтобы интересующая нас переменная перестала быть равной нулю.

Завершая раздел, посвященный задачам нелинейного программирования, следует сказать несколько слов о настройке параметров работы программы Поиск решения. Эти настройки могут оказаться полезными при решении задач нелинейного программирования.

Рис. 25. Окно настройки параметров программы Поиск решения

Получить некоторое представление о смысле параметров, которые можно использовать для настройки программы Поиск решения, можно, если нажать кнопку Справка. Здесь мы обсудим лишь наиболее важные для практической работы настройки.

Значение в поле Сходимость используется для завершения процесса поиска решения. Если изменение целевой функции на протяжении пяти итераций меньше, чем указано в окне, то процедура поиска решения завершает работу. Поэтому, если программа долго не может найти решение, следует увеличить значение числа в поле Сходимость.

Переключатель панели Оценки по умолчанию установлен в положение линейная. Квадратичная оценка является более точной, но требует для выполнения вычислений большего времени.

То же самое можно сказать и относительно установки переключателей в поле Разности. Прямые разности используются для гладких непрерывных функций, а центральные – для функций, имеющих разрывную производную. Последний способ точнее, но требует больше вычислений.

При проведении оптимизации можно задать также метод поиска решения. По умолчанию выбран метод Ньютона. Альтернативный метод сопряженных градиен-

41

тов требует большего числа вычислений, но реже обращается к оперативной памяти при той же заданной точности вычислений. В итоге для больших нелинейных задач метод сопряженных градиентов зачастую находит решение быстрее, нежели метод Ньютона.

Значение в поле Относительная погрешность определяет, насколько точно левая часть должна соответствовать правой части ограничения, чтобы ограничение считалось выполненным как равенство.

Кнопка Сохранить модель позволяет задать ссылку на область ячеек, предназначенную для хранения модели оптимизации, а кнопка Загрузить модель – задать ссылку на область ячеек, содержащих загружаемую модель. Эти возможности следует использовать, если на рабочем листе располагается более чем одна оптимизационная задача. Если на рабочем листе модель одна, то она загружается автоматически.

Многокритериальная оптимизация

В рассмотренных выше задачах математические модели имели одну целевую функцию. На практике очень часто нужно найти экстремальные значения нескольких экономических показателей. Например, при составлении долгосрочного плана развития предприятия могут ставиться задачи: а) максимизации прибыли, б) захвата рынков сбыта продукции, в) максимизации основного капитала на конец планового периода и т. д.

Эти цели не сопоставимы в том смысле, что достижение одной цели препятствует достижению другой цели: максимизация прибыли приведет к снижению расходов на рекламу, что не способствует продвижению товара на рынках сбыта. Поэтому ставится задача нахождения компромиссного решения модели, в котором значения всех рассматриваемых экономических показателей были бы приближены к экстремальным значениям.

Математические алгоритмы решения такого рода задач все еще недостаточно разработаны и для практического решения задач используют три основных подхода.

1.Производится ранжирование показателей, в результате чего они располагаются в порядке убывающей значимости. Затем модель оптимизируется по первому, наиболее важному показателю. После того, как решение получено, приступают к оптимизации второго показателя. Для того, чтобы найденное значение первого показателя не претерпело при этом значительных изменений, определяется интервал допустимых его значений, который добавляется к числу ограничений новой модели, в которой ищется оптимальное значение второго показателя. Процесс продолжается до тех пор, пока не будут исчерпаны все цели.

2.Строится единый интегральный показатель эффективности посредством суммирования произведений (свертки) целевых функций для каждого из подлежащих оптимизации экономических показателей и весовых коэффициентов, значение которых определяет лицо, принимающее решение (ЛПР). Например, если

42

делены веса 0,75 и 0, 25 для первой и второй целей, то может быть поставлена задача 0,75 f1(x1, x2 , , xn ) 0,25 f2 (x1, x2, , xn ) max .

3.Если заранее известны желаемые значения некоторых экономических показателей, то целевые функции для них можно сразу перевести в ограничения. Для оптимизации оставшихся показателей можно использовать один из двух описанных выше подходов.

Вдействительности подходы, описанные в пунктах 1 – 3 . не являются строгими рекомендациями, а задают лишь некоторые направления построения моделей многокритериальной оптимизации. В частности, на практике часто бывает удобно ввести дополнительные переменные отклонения для которых ставится задача минимизации. Эту методику решения задач многокритериальной оптимизации рассмотрим на примере.

Пример 3.12

Производственное предприятие производит лодочные моторы. Экономические характеристики производственного процесса приведены в таблице

Маркетинговые исследования показали, что спрос на лодочные моторы марки «Пермь» составляют не менее тысячи в год.

Найти оптимальное решение по годовому производству лодочных моторов, удовлетворяющее следующим условиям: а) прибыль и количество выпускаемых моторов должны быть максимальными; б) себестоимость производства должна быть минимальной.

Решение

Если обозначить x1 и x2 годовое производство моторов (тыс. шт.), то математическая модель задачи может быть записана в виде

43

x1 0, x2 0.

Решим задачу по каждой целевой функции в отдельности. В итоге получим три различных решения, которые представлены в таблице.

Очевидно, что все три условия сразу выполнить невозможно. Поэтому для решения этой многокритериальной задачи применим метод, который является развитием третьего подхода.

Поскольку оптимальные значения целевых функций известны, для определения компромиссного решения введем новую переменную x3 , которая будет

характеризовать степень отклонения компромиссного решения от каждого из оптимальных решений, и потребуем нахождения минимального значения величины x3 . Исходные целевые функции в модели (3.28) превратим в ограни-

чения. В итоге получаем модель многоцелевой оптимизации

x3 min;

x1 x2 4,125 x3 4,125;

x2 1;

x1 0, x2 0, x3 0.

44

Если бы значение x3 оказалось равным нулю, то область допустимых ре-

шений задачи, определяемая ограничениями (3.29), была бы такой, что для точек этой области значения целевых функции из приведенной выше таблицы были бы лучше оптимальных.

Очевидно, что это невозможно. Приемлемым окажется решение с минимально возможным значением x3 .

Выполняя оптимизацию модели (3.29) с помощью программы Поиск решения, получаем, что для оптимизации всех поставленных задач предприятию следует производить 1 071 мотор марки «Урал» и 1 000 мотором марки «Пермь».

На практических занятиях будет рассмотрен еще один важный для решения прикладных задач эвристический метод многокритериальной оптимизации, ко-

торый носит название аналитического иерархического процесса. Этот метод позволяет решать задачу выбора одного из вариантов, когда следует учесть множество различных факторов: например, при приобретении нового автомобиля или компьютера, выборе места работы после окончания вуза и т. д.

Понятие риска. Постановка задачи о принятии решения в условиях неопределенности и риска

Отсутствие точных данных относительно будущих событий – характерная особенность большинства управленческих моделей. Например, требуется оптимизировать доходность некоторого актива путем приобретения акций нескольких промышленных компаний. Менеджер банка может получить сведения о доходности того или иного пакета акций в прошлом, однако доходность этих акций в будущем является случайной величиной, и менеджер банка вынужден принимать решение в условиях риска.

При принятии решения в условиях неопределенности может встретиться две основных ситуации:

1)требуется принять решение, когда каждый из возможных исходов имеет известную для ЛПР или вычисляемую вероятность реализации;

2)требуется принять решение, когда имеется множество возможных исходов,

но их вероятности совершенно неизвестны или не имеют смысла. Проблема риска и прибыли является одной из ключевых в экономике. По-

этому желательно дать численное определение понятия риска. Это достаточно просто сделать для ситуации 1), когда известны вероятности реализации различных исходов.

В этом случае за меру риска коммерческого или финансового решения обычно принимают среднеквадратическое отклонение (квадратный корень из дисперсии) показателя, характеризующего экономическую эффективность решения.

Чаще всего показателем эффективности решения является прибыль. Поэтому при принятии решения в условиях неопределенности следует оценивать как ожидаемую прибыль, так и среднеквадратическое отклонение прибыли от ожидаемой величины (риск). Рассмотрим понятие риска на конкретном примере.

45

Пример 3.13

Акционерному обществу предлагается два рисковых проекта:

Какой проект должны выбрать акционеры и почему?

Решение

Для оценки эффективности рассматриваемых инвестиционных проектов вычислим ожидаемую прибыль и величину риска получения прибыли. Ожидаемая прибыль x1 и x2 для первого и второго проектов равны

Таким образом, математические ожидания прибыли для обоих проектов оказались равными.

Найдем теперь риск получения средней прибыли, вычислив среднеквадратические отклонения прибыли 1 и 2 для обоих проектов. Учитывая, что

дисперсия вычисляется по формуле

n

2 (xi x )2 pi ,

i 1

находим 12 40 , 22 2 000 . Таким образом, среднеквадратическое отклонение для первого проекта 1 6,32 млн руб., а для второго – 2 44,72

млн руб. Иными словами, при той же самой средней прибыльности 50 млн руб. первый проект обладает существенно меньшей вариабельностью (риском).

Рассмотренный выше пример можно назвать игрой с природой, поскольку предполагается, что доходность складывается под действием случайных факторов. Акционерную компанию можно назвать игроком, а ожидаемую прибыль – выигрышем игрока.

Используя терминологию теории игр, можно дать более общее определение понятия риска. Риск – это разность между результатом, который можно получить, если знать действительное состояние природы, и результатом, который будет получен при выборе i той стратегии игрока. Это определение риска можно применить и в случае 2), когда имеется множество возможных исходов, но их вероятности совершенно неизвестны.

Основные определения математической теории игр

Если несколько изменить условие задачи примера 3.13, предположив, что те же самые проекты намереваются реализовать и другие акционерные компании, то мы получим конфликтную игровую модель, в которой участники (игроки) имеют кон-

46

фликтные интересы (увеличение выигрыша одного игрока приводит к уменьшению выигрыша другого игрока).

Математическая теория игр является разделом математики, изучающей принятие решений в конфликтных ситуациях.

Определим основные понятия теории игр.

Игра – упрощенная формализованная модель конфликтной ситуации. Игрок

– одна из сторон в игровой ситуации. В зависимости от постановки задачи, стороной может выступать коллектив или даже целое государство.

Каждый игрок может иметь свои стратегии. Стратегией i го игрока xi

называется одно из его возможных решений из множества допустимых решений этого игрока.

По количеству стратегий игры делятся на конечные, в которых число стратегий ограничено, и бесконечные, которые имеют бесконечно много различных стратегий.

Каждый из n участников игры может выбирать свою стратегию. Совокупность стратегий x x1, x2 , , xn , которые выбрали участники игры, называется

игровой ситуацией.

Оценить ситуацию x с точки зрения преследуемых ЛПР целей можно, построив целевые функции (или критерии качества), ставящие в соответствие каждой ситуации x числовые оценки f1(x), f2 (x), , fn (x) (например, доходы

фирм в ситуации x или их затраты и т. д.).

Тогда цель i – го ЛПР формализуется следующим образом: выбрать такое свое решение xi , чтобы в ситуации x x1, x2 , , xn число fi (x) было как можно

большим (или меньшим). Однако достижение этой цели от него зависит лишь частично, поскольку другие участники игры влияют на общую ситуацию x с целью достижения своих собственных целей (оптимизируют свои целевые функции). Значение целевой функции в той или иной игровой ситуации можно назвать выигрышем игрока в этой ситуации.

По характеру выигрышей игры можно разделить на игры с нулевой и ненулевой суммой. В играх с нулевой суммой сумма выигрышей в каждой игровой ситуации равна нулю. Игры двух игроков с нулевой суммой называются антагонистическими. В этих играх выигрыш одного игрока равен проигрышу другого.

В играх с ненулевой суммой в выигрыше или проигрыше могут оказаться все участники игры.

По виду функции выигрышей игры можно разделить на матричные, биматричные, непрерывные, сепарабельные и т. д.

Матричными играми называются конечные игры двух игроков с нулевой суммой. В этом случае номер строки матрицы соответствует номеру стратегии Ai

игрока 1, а номер столбца – номеру стратегии B j игрока 2.

Элементами матрицы aij является выигрыш игрока 1 для ситуации (реализации стратегий) Ai Bj . В силу того, что рассматривается матричная игра с нулевой суммой, выигрыш игрока 1 равен проигрышу игрока 2.

47

Можно показать, что всякая матричная игра с известной матрицей платежей сводится к решению задачи линейного программирования.

Поскольку в прикладных задачах экономики и управления ситуации, сводящиеся к матричным играм, встречаются не очень часто, мы не будем останавливаться на решении этих задач.

Биматричная игра – это конечная игра двух игроков с ненулевой суммой. В этом случае для каждой игровой ситуации Ai Bj каждый из игроков имеет свой

выигрыш aij для первого игрока и bij – для второго игрока. К биматричной игре

сводится, например, поведение производителей на рынках несовершенной конкуренции (дуополия). Анализу этой проблемы посвящена тема 6 настоящего учебного пособия.

По степени неполноты информации, которой обладают ЛПР, игры делятся на стратегические и статистические .

Стратегические игры – это игры в условиях полной неопределенности. Статистические игры – это игры с частичной неопределенностью. В ста-

тистической игре всегда имеется один активный игрок, имеющий свои стратегии и цели. Другим игроком (пассивным, не преследующим своих целей) является природа. Этот игрок реализует свои стратегии (состояния природы) случайным образом, причем вероятность реализации того или иного состояния можно оценить с помощью статистического эксперимента.

Поскольку с теорией статистических игр тесно связана теория принятия экономических решений, то в дальнейшем мы ограничимся рассмотрением только этого класса игр.

Принятие решений в условиях неопределенности

Методы принятия решений в играх с природой зависят от характера неопределенности, точнее, от того, известны или нет вероятности различных состояний (стратегий) природы. Если вероятности различных состояний природы неизвестны, то мы имеем дело с принятием решения в условиях неопределенности, а если известны или поддаются оценке, то реализуется ситуация принятия решения в условиях риска. Ниже мы рассмотрим оба этих случая.

Допустим, что нам известны возможные состояния (стратегии) природы, но полностью отсутствует информация об их вероятности. В этих условиях для принятия решения следует составить платежную матрицу. Для конкретности рассмотрим числовой пример.

Пример 3.14

Рабочий поселок имеет котельную, которая обеспечивает теплом и горячей водой поселок зимой. Руководителю поселковой администрации необходимо закупить уголь для работы котельной зимой. Часть угля можно купить в конце лета, поскольку летом он дешевле, а часть зимой. В июне и июле угольный склад не охраняется, и остатки угля с прошлой зимы теряются. Известно, что зима может быть мягкой, средней и суровой, и в зависимости от этого

48

может потребоваться разное количество угля. Глава администрации для трех своих возможных стратегий рассчитал матрицу выигрышей (млн руб.).

Какую из возможных стратегий должен выбрать глава администрации?

Рассмотрим на этом конкретном примере возможные методики принятия решения в условиях неопределенности.

В ситуации полной неопределенности однозначного решения задачи не существует. При принятии решения ЛПР может пользоваться одним из возможных критериев: Лапласа, максимакса, Вальда (максимина), Сэвиджа, Гурвица. Рассмотрим последовательно применение этих критериев к решению поставленной задачи.

Критерий Лапласа исходит из предположения, что все стратегии природы равновероятны, Поскольку в рассматриваемой задачи их три, то вероятность реализации каждой из них pi 0,333, i 1, 2, 3. Поэтому ожидаемый выигрыш

для каждой из трех стратегий

3

fi aij p j . j 1

Подставляя сюда значения коэффициентов aij и вероятности p j , получаем:

Таким образом, согласно критерию Лапласа, оптимальной получается вторая стратегия, поскольку при этой стратегии ожидаемый выигрыш больше.

Критерий максимакса, или критерий крайнего оптимизма, исходит из того, что будут реализованы самые благоприятные условия. Для каждой стратегии игрока выбирается наибольший выигрыш. Затем из максимальных выигрышей выбирается самый большой. Этот алгоритм эквивалентен выбору наибольшего элемента матрицы выигрышей. Очевидно, что согласно этому критерию максимаксный выигрыш составит 8 (вторая стратегия игрока и вторая стратегия природы).

Согласно критерию Вальда (максимина), или критерию крайнего пессимизма,

выбирается наибольший. В рассматриваемом случае это будет выигрыш, равный 3 (вторая стратегия игрока).

Этот критерий является критерием крайнего пессимизма потому, что при оценке выигрыша здесь предполагается, что природа ведет себя злонамеренно, реализуя для каждой стратегии игрока наихудшую ситуацию.

49

Критерий минимаксного риска Сэвиджа исходит из анализа матрицы рисков, которая может быть получена из матрицы выигрышей.

В данном случае риском игрока rij при выборе им стратегии Ai и состоянии природы j можно назвать разность между выигрышем, который мог бы по-

лучить игрок, если бы он обладал информацией о состоянии природы, и выигрышем, который он получает согласно матрице платежей.

Поясним сказанное на примере. Рассмотрим первую стратегию игрока и первое состояние природы. Если бы игрок знал, что реализуется первое состояние природы, то он бы выбрал свою третью стратегию и получил выигрыш 4. При отсутствии этого знания его выигрыш составит 1. Таким образом, риск для этой ситуации равен 3.

Сказанного вполне достаточно, чтобы сформулировать алгоритм получения матрицы рисков из матрицы платежей. В каждом столбце матрицы платежей следует найти максимальный элемент, обозначив его j . Тогда матрица рисков

равна просто разности rij j aij . Запишем матрицу рисков R для рассматриваемого примера

Дальнейший выбор оптимальной стратегии аналогичен выбору стратегии по критерию Вальда, с тем отличием, что для анализа используется не матрица платежей (3.30), а матрица рисков (3.31). Сначала для каждой из стратегий иг-

стратегию, обеспечивающую минимальный риск. Таким образом, оптимальной, как и в предыдущих случаях, будет вторая стратегия игрока.

Критерий пессимизма – оптимизма Гурвица при выборе стратегии рекомен-

дует пользоваться неким средним результатом, характеризующим состояние между крайним оптимизмом и крайним пессимизмом.

Как и в случае поиска максиминной стратегии, для каждой стратегии игрока Ai находим величину i по формуле

В выражении (3.32) величина 0 p 1 играет роль показателя пессимизма. При p 0 в строке отыскивается максимальный выигрыш (предельный оптимизм), а при p 1– минимальный (предельный пессимизм). После того как для каждой стратегии величины i найдены, оптимальной считается та стратегия, для которой величина i максимальна. Применим этот критерий к платежной матрице (3.30), полагая значение p 0,5 . Выполняя простые вычисления, получаем:

50