2.2.1. Оценка параметров регрессионной модели

Исходными данными для получения оценок параметров регрессионной модели технической системы (т. е. оценок искомых коэффициентов регрессии) является информация о значения управляемых факторов(или неуправляемых — при проведении пассивного эксперимента) и функции откликаY. Эту информацию можно представить в виде матрицы Х значений факторов во всех N опытах, предусмотренных спектром плана эксперимента, и вектора-столбца полученных в этих опытах значений функции откликаY:

(107)

(108)

где — вектор-строка значений факторов в 1-м опыте;X_ij — значение j-го фактора в i-м опыте; n — количество факторов; N — количество опытов; у_i — значение функции отклика Y в i-ом опыте (если проводились параллельные опыты, т. е. осуществлялось дублирование опытов, то вместо y_i используются оценки их математических ожиданий, т. е. выборочные средние ).

Значения базисных функций во всех опытах представляют собой матрицу F, называемую матрицей базисных функций:

(109)

где f_ik — значение k-ой базисной функции в i-ом опыте; – вектор-строка значений базисных функций вi-ом опыте.

Используя информацию об X, иF, необходимо найти оценки коэффициентов регрессии, представляемые вектором-столбцом

(110)

где b_k — значение оценки коэффициента регрессии при базисной функции .

Так как функция отклика Y — случайная величина, поскольку на ее значения в различных опытах оказывает влияние случайная помеха , то оценки коэффициентов регрессии будут случайными величинами.

Уравнение регрессии устанавливает зависимость между оценкой математического ожидания функции отклика и факторами= (x₁, x₂,..., x_n). Общий вид этой зависимости

(111)

В связи с наличием помехи значение функции отклика в i-м опыте у_i будет отличаться от . Для определения у_i можно составить выражение

(112)

где _i — невязка уравнения регрессии в i-м опыте.

Невязка характеризует отклонение значений функции отклика в опытах от получаемых с помощью регрессионной модели (111). Она возникает по двум причинам: из-за ошибки эксперимента и из-за непригодности (приближенности) выбранной структуры факторной математической модели. Причем, эти причины смешаны и нельзя сказать, какая из них преобладает.

Если постулировать, что модель пригодна, то невязка будет порождаться только ошибкой опыта. Тогда для определения коэффициентов уравнения (111) невязку надо минимизировать. Для этого в регрессионном анализе используется метод наименьших квадратов (МНК). Составляется функция, представляющая собой сумму квадратов невязок, и осуществляется ее минимизация, т.е.

(113)

Подставим значение _i из выражения (112):

(114)

В выражении (114) коэффициенты b_k рассматриваются как неизвестные переменные, которые наилучшим образом соответствуют полученным результатам эксперимента. Значения этих коэффициентов, при которых достигается минимум функции Е, имеет место при равенстве нулю частных производных этой функции по переменным b₀, b₁,..., b_d:

После преобразований получим систему линейных неоднородных алгебраических уравнений относительно искомых оценок коэффициентов регрессии b₀, b₁,..., b_d:

(115)

Очевидно, что коэффициенты при неизвестных переменных этой системы уравнений являются элементами матрицыФ, определяемой из выражения

(116)

в котором F представляет собой матрицу базисных функций (109). Значения элементов матрицы F известны из проведенного эксперимента. Следовательно, элементы матрицы Ф оказываются известными коэффициентами системы уравнений (115). Выпишем матрицу Ф:

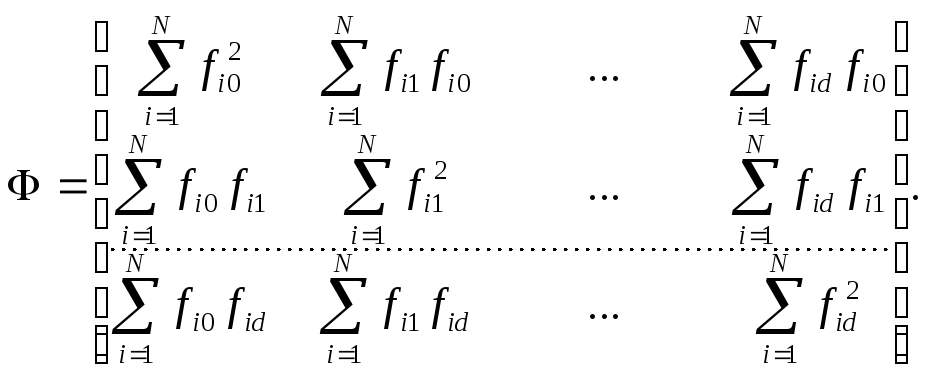(117)

Матрицу Ф называют информационной матрицей Фишера. Она содержит (d +1) строк и (d +1) столбцов, причем элемент j-ой строки k-го столбца представляет собой сумму МатрицаФ симметрична относительно главной диагонали, что упрощает составление системы алгебраических уравнений (115) для регрессионной модели.

Систему уравнений (115) можно также записать в матричной форме:

(118)

Система уравнений (115) имеет единственное решение, если определитель матрицы Ф не равен нулю. В этом случае матрица Ф будет не вырожденной. Выполнение пятой предпосылки регрессионного анализа, изложенной в предыдущем параграфе, исключает возникновение вырожденности.

Решение системы уравнений (115) обычно осуществляют методом Гаусса. При небольшом числе определяемых коэффициентов b_k можно использовать правило Крамера.

Полученные методом наименьших квадратов оценки b₀, b₁,..., b_d действительных значений коэффициентов регрессии ₀, ₁,..., _d обладают следующими свойствами:

1) математические ожидания оценок

т. е. оценки b_j несмещенные;

2) дисперсии оценок коэффициентов регрессии минимальны и равны

(119)

а корреляционный момент

(120)

где С_jj, С_jk — элементы матрицы Ф^-1, обратной к информационной; — дисперсия случайной помехи;

3) оценки b₀, b₁,..., b_d подчиняются совместному (d + 1) -мерному нормальному распределению.