Фундаментальная система решений и построение общего решения однородного линейного уравнения.

Пусть имеется система функций ,, …,, определенных на некотором интервале.

Определение. Функции ,, …,называются линейно зависимыми на интервале, если существуют постоянные,, …,такие, что на этом интервале выполняется тождество пох:

++…+,

причем хотя бы одно из чисел отлично от нуля.

Если это тождество имеет место только при ==…==0, то функции,, …,называются линейно независимыми на интервале.

Совокупность п решений ,, …,,однородного линейного уравнения (11), линейно независимых а интервале, называетсяфундаментальной системой решений этого уравнения в интервале .

Сформулируем признак линейной независимости п частных решений однородного линейного уравнения п-го порядка. Для этого введем в рассмотрение определитель, составленный из данных частных решений и их производных до порядка п-1 включительно:

.

Этот определитель называется определителем Вронского решений ,, …,или вронскианом.

Теорема 1 (необходимое условие линейной зависимости функций). Если функции ,, …,, имеющие производные до порядкап-1 включительно, линейно зависимы на интервале , то на этом интервале определитель Вронского тождественно равен нулю.

Обратное утверждение вообще говоря не верно.

Пример. Система функций - линейна независима на любом множестваХ.

Решение. Определитель Вронского для данной системы функций:

Следовательно, по теореме 1 данная система функций действительно является линейно независимой.

Теорема 2. Для того, чтобы решения

, , …,,(12)

были линейно независимы в , т.е. в интервале непрерывности коэффициентов уравнения (11), необходимо и достаточно, чтобыне обращался в нуль ни в одной точке из.

Доказательство. Необходимость. Пусть решения (12) линейно независимы в . Предположим, что, где.

Построим однородную линейную систему п уравнений

(13)

с неизвестными функциями ,, …,. Определитель этой системы есть. Так как он равен нулю, то эта система имеет ненулевое решение=,=, …,=, т.е. хотя бы одно из чисел,, …,не равно нулю.

Построим линейную комбинацию решений (12), взяв в качестве коэффициентов числа ,, …,. Получим решение

у=++…+. (14)

Это решение удовлетворяет нулевым начальным условиям ,, …,при, как это видно из системы (13). Следовательно, в силу единственности решения задачи Коши, которая имеет место вследствие непрерывности коэффициентов уравнения (11), решение (14) должно быть нулевым, т.е.

++…+0,.

Так как среди чисел ,, …,хотя бы одно отлично от нуля, то это тождество означает, что решения (12) линейно зависимы в. Пришли к противоречию, следовательно,не обращается в нуль ни в одной точке из.

Достаточность. Предположим, что не обращается в нуль в, но решения (12) линейно зависимы в, так что имеет место тождество

++…+,,

где, например, . Тогда

,

откуда

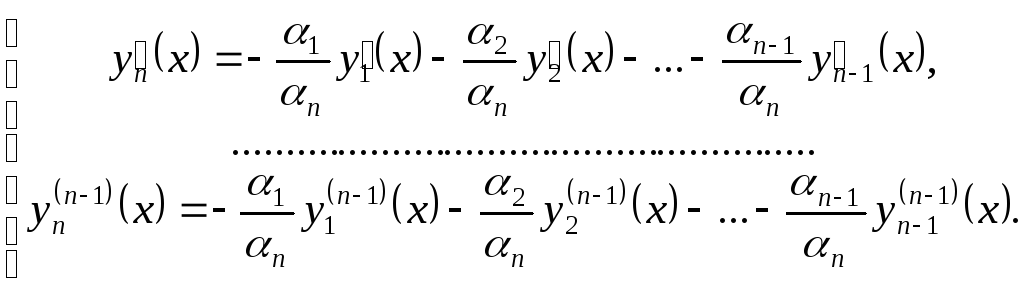
Поэтому мы получаем, что определитель Вронского

представляет собой определитель, у которого элементы последнего столбца являются линейными комбинациями элементов других столбцов. Такой определитель, как известно, равен нулю. Таким образом, мы пришли к противоречию. Следовательно, решения (12) линейно не зависимы в . Теорема доказана полностью.

Значение определителя Вронского п решений (12) однородного линейного уравнения (11) тесно связано с самим уравнением, а именно: имеет место формула Остроградского-Лиувилля:

.

Из этой формулы видно, что определитель Вронского п решений уравнения (11) обладает следующими свойствами:

1. Если обращается в нуль в одной точке из интервала, то он равен нулю во всех точках этого интервала.

2. Если не равен нулю в одной точкеиз интервала, то он отличен от нуля во всех точках этого интервала.

Таким образом, для того, чтобы п решений (12) составляли фундаментальную систему решений уравнения (11) в интервале , достаточно, чтобы их определитель Вронского был отличен от нуля в одной точке.