Лекция №7

Тема: Линейные уравнения второго порядка с постоянными коэффициентами и колебательные явления

Вопросы:

1. Задача, приводящая к уравнению колебаний. Уравнения свободных и вынужденных колебаний.

2. Свободные колебания в среде без сопротивления.

3. Влияние наличия сопротивления среды на характер движений.

4. Вынужденные колебания под действием силы, носящей синусоидальный характер. Нерезонансный и резонансный случаи.

Р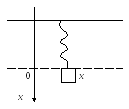ассмотрим следующую задачу: на пружину, закрепленную с одной стороны подвешен груз массы m. Предположим, что в положении равновесия центр масс этого груза находится на некотором расстоянии от точки крепления. При выведении груза из равновесия центр масс смещается. Пусть отклонение центра масс от положения равновесия равно х. В процессе колебания х меняется и представляет собой функцию от t: . Рассмотрим силы, действующие на груз:

1) сила упругости, притягивающая груз к началу координат и имеющая проекцию на ось х, равную , , k – коэффициент упругости пружины;

2) сила сопротивления среды, в которой происходят колебания, которую будем считать пропорциональной первой степени скорости: , с – коэффициент сопротивления среды;

3) внешняя сила: .

Применяя второй закон Ньютона, получим дифференциальное уравнение движения:

,

или, разделив обе части на m, перепишем его в виде

, (1)

где , , .

Таким образом, мы получили неоднородное линейное уравнение с постоянными коэффициентами. Проинтегрировав его, найдем закон движения рассматриваемой точки. Так как наибольший интерес имеют случаи, когда движения, определяемые уравнением (1), представляют собой колебания груза около положения , то уравнение (1) называют уравнением колебаний. При этом, если внешняя сила отсутствует, так что , то уравнение (1) принимает вид

(2)

и называется уравнением свободных колебаний. Дифференциальное уравнение (1), в котором тождественно, называется уравнением вынужденных колебаний.

Уравнение (1) всегда интегрируется, так как соответствующее однородное уравнение (2) всегда интегрируется в элементарных функциях, а применяя метод Лагранжа, можно найти общее решение уравнения (1) при любой непрерывной функции , т.е. для любой силы , если она непрерывная функция от времени t.

Рассмотрим подробно все возможные случаи:

1. Случай отсутствия внешней силы (свободные колебания).

Рассмотрим уравнение (2). Выясним, как влияют параметры , на характер движений (решений уравнения). Предположим сначала, что , т.е. колебания происходят в среде без сопротивления. В этом случае уравнение (2) примет вид

. (3)

Его характеристическим уравнением будет

,

откуда

,

поэтому

, ,

и общее решение примет вид

.

Введем вместо новые произвольные постоянные А и , положив

, .

Получим

. (4)

Такое движение называется гармоническим колебанием. Как видно из формулы (4), оно является периодическим движением с периодом и частотой . Число А называется амплитудой, а  - начальной фазой колебания (4). (Аргумент синуса - фаза гармонического колебания).

В

х

се движения, определяемые уравнением (3) ограничены, так как

, при всех .

Любым начальным условиям , при в силу теоремы Пикара о существовании и единственности решения задачи Коши для линейного уравнения п-го порядка соответствует одно движение, которое входит в формулу (4), при соответствующих значениях амплитуды и начальной фазы, которые можно определить, подставив начальные данные в систему:

Получаем

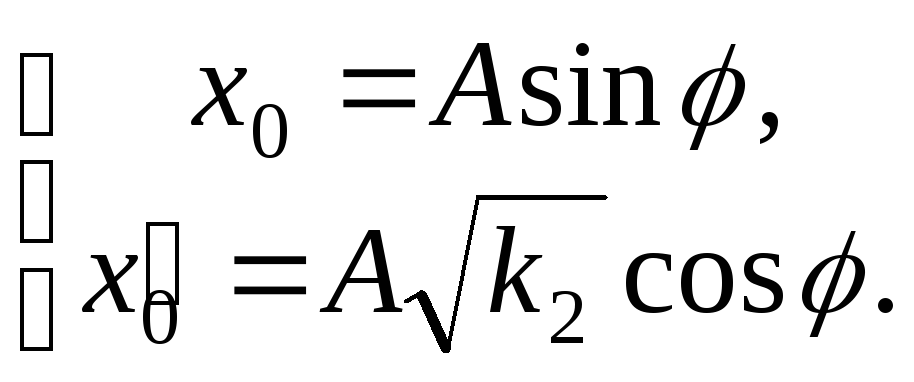
Откуда

x

В частности, если точка (груз) начинает движение из положения без начальной скорости, т.е. , то 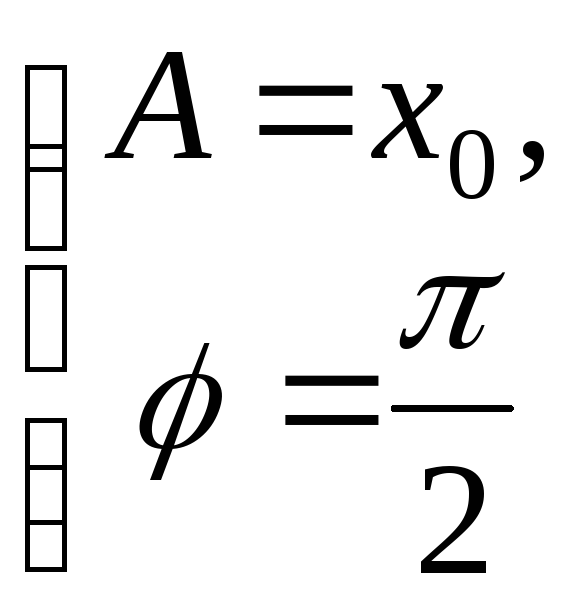и движение имеет вид

или .

Если точка начинает движение из положения с начальной скоростью , то и соответствующим движением будет .

Если оба начальных значения равны нулю, то А = 0 и движение (4) примет вид , т.е. выродится в состояние покоя. Это будет единственное движение, удовлетворяющее нулевым начальным условиям. Очевидно, скорость этого движения равна нулю при всех t. Состояние покоя обладает следующим свойством: все движения, у которых начальные значения , и не равны одновременно нулю, но достаточно малы, будут при всех сколь угодно мало отклоняться от состояния покоя и иметь сколь угодно малую скорость. Действительно, эти движения имеют вид

.

Их скорость определяется формулой

.

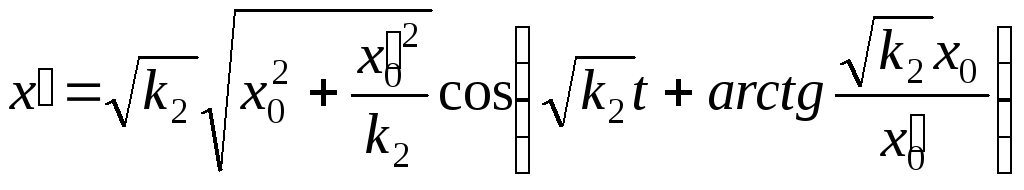Поэтому

,

,

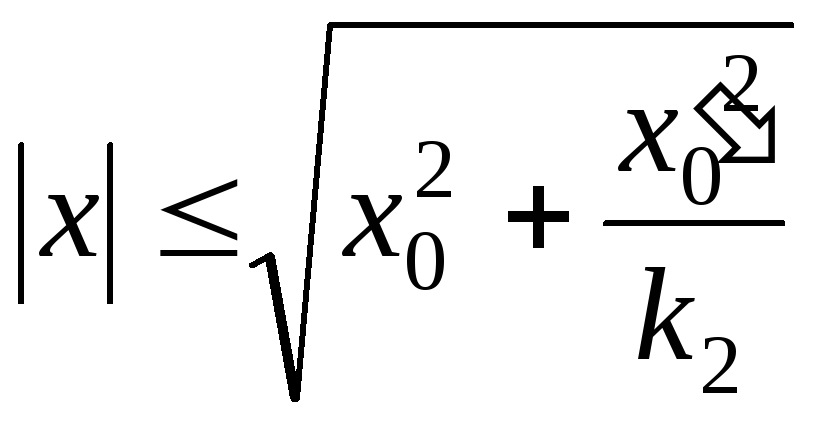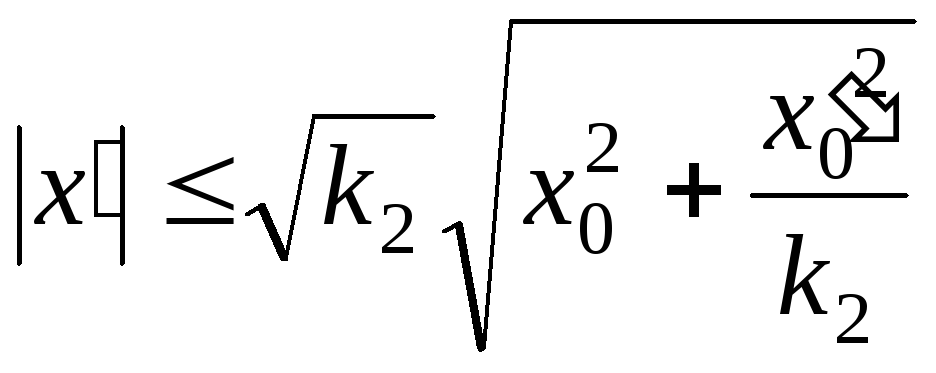следовательно, при всех , если и достаточно малы, то х и х’ будут сколь угодно малыми.

Предположим теперь, что в уравнении (2) , т.е. колебание происходит в среде с сопротивлением.

Выясним как влияет наличие на характер колебаний. Для этого найдем общее решение уравнения (2).

Характеристическое уравнение

имеет корни

.

Возможны три случая:

1. , т.е. . В этом случае оба корня характеристического уравнения действительные и отрицательные. Общее решение уравнения (2) имеет вид

.

Движения, соответствующие этим решениям являются апериодическими. Причем при , колебания отсутствуют при большом коэффициенте сопротивления среды и малом коэффициенте жесткости пружины.

2. , тогда . Общее решение примет вид

.

Движения, соответствующие этим решениям также будут апериодическими и при .

3. , т.е. . В этом случае характеристическое уравнение имеет сопряженные комплексные корни с отрицательной действительной частью

.

Поэтому общее решение примет вид

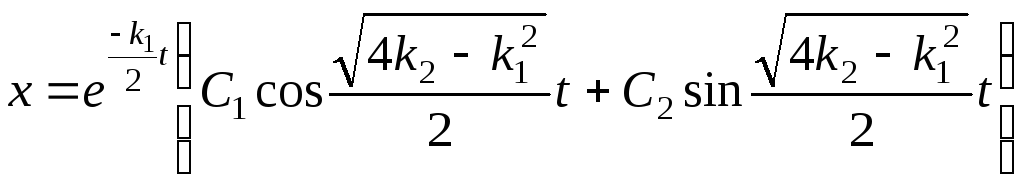
или

.

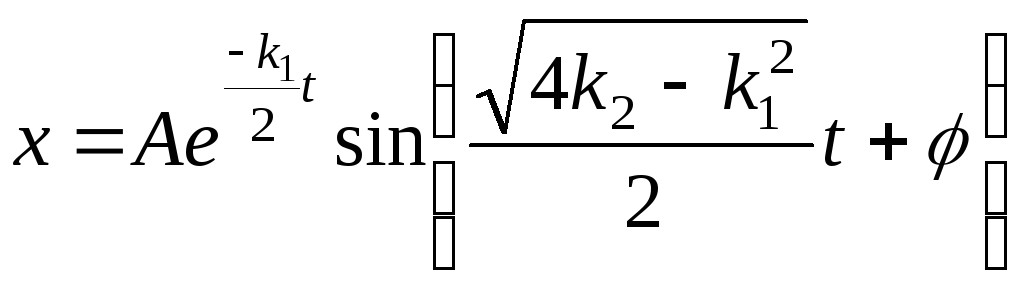Движение, соответствующее этому решению, называется затухающим гармоническим колебанием с периодом и частотой , амплитудой и начальной фазой . В отличие от гармонического колебания (4), здесь амплитуда уже непостоянна, причем она ограничена, так как , и стремиться к нулю при . Число А называется начальной амплитудой, а - коэффициент затухания. Множитель характеризует быстроту затухания.

Начальная амплитуда и начальная фаза определяются из начальных условий. При этом , поэтому графики ненулевых решений заключены между графиками показательных функций и .

При , - незатухающие гармонические колебания.

Таким образом, наличие сопротивления среды () видоизменяет характер колебаний, причем пока сопротивление сравнительно невелико (), движения остаются периодическими, затухая при . При большом сопротивлении среды движения становятся апериодическими.