
Госы 5к Надя / ДУ / Лекция 3
.docЛекция №3
7. Уравнения в полных дифференциалах.
Вопросы:
1. Понятие дифференциального уравнения в полных дифференциалах. Необходимое и достаточное условие того, что уравнение является уравнениям в полных дифференциалах.
2. Уравнения, сводящиеся к уравнениям в полных дифференциалах. Интегрирующий множитель. Частные случаи нахождения интегрирующего множителя.
3. Уравнения Лагранжа и Клеро.
Запишем уравнение в дифференциальной форме
![]() . (1)
. (1)
Если левая часть
уравнения (1) является полным дифференциалом
некоторой функции
![]() ,
т.е.
,
т.е.
![]() ,
,
то уравнение (1) называется уравнением в полных дифференциалах.
Так как уравнение в полных дифференциалах можно записать в виде
![]() ,
,
то его общим интегралом будет
![]() .
.
В общем случае
определить является ли дифференциальное
уравнение уравнением в полных
дифференциалах трудно. Укажем признак,
позволяющий ответить на этот вопрос, а
также один из способов нахождения
функции
![]() .
.
Предположим, что
в уравнении (1) функции
![]() и
и
![]() непрерывны в некоторой односвязной
области G,
например, в прямоугольнике с центром в
заданной точке
непрерывны в некоторой односвязной
области G,
например, в прямоугольнике с центром в
заданной точке
![]() ,
и не обращаются одновременно в нуль в
этой точке. Кроме того, предположим, что
в области G
существуют непрерывные частные
производные
,
и не обращаются одновременно в нуль в
этой точке. Кроме того, предположим, что
в области G
существуют непрерывные частные
производные
![]() и
и
![]() .
.
Теорема.
Для того чтобы при сделанных предположениях
относительно функций
![]() и
и
![]() уравнение (1) было уравнением в полных
дифференциалах, необходимо и достаточно,
чтобы в области G
выполнялось тождество
уравнение (1) было уравнением в полных
дифференциалах, необходимо и достаточно,
чтобы в области G
выполнялось тождество
![]() . (2)
. (2)
Доказательство. Докажем необходимость условия (2). Пусть уравнение (1) – уравнение в полных дифференциалах. Тогда
![]() ,
,
так что
![]() ,
,
![]() . (3)
. (3)
Дифференцируя тождества (3) соответственно по у и по х, получим
![]() ,
,
![]() .
.
Но в силу непрерывности
частных производных
![]() и
и
![]() правые части тождеств равны по теореме
Шварца о смешенных производных, а,
следовательно, равны и левые части, т.е.
имеет место тождество (2).
правые части тождеств равны по теореме
Шварца о смешенных производных, а,
следовательно, равны и левые части, т.е.
имеет место тождество (2).
Докажем теперь
достаточность условия (2). Пусть это
условие выполнено. Покажем, что тогда
можно найти такую функцию
![]() ,
чтобы выполнялось равенство
,
чтобы выполнялось равенство
![]() ,
или равносильные ему тождества (3).
,
или равносильные ему тождества (3).
Выберем сначала
функцию
![]() так, чтобы она удовлетворяла первому
из условий (3). Т.е. в качестве функции
так, чтобы она удовлетворяла первому
из условий (3). Т.е. в качестве функции
![]() можно выбрать
можно выбрать
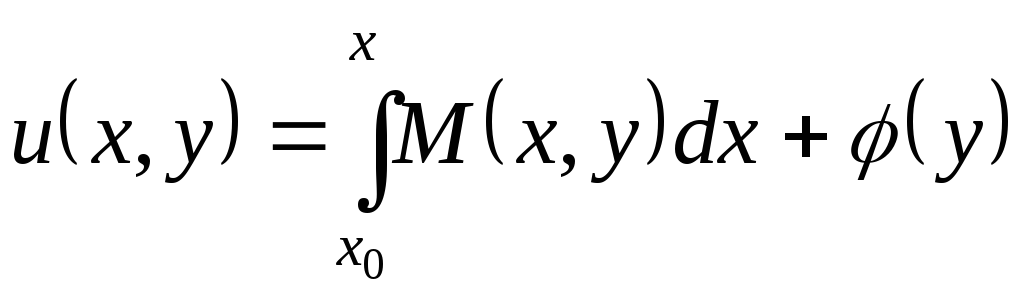 , (4)
, (4)
где
![]() - произвольная непрерывно дифференцируемая
функция от у.
- произвольная непрерывно дифференцируемая
функция от у.
Определим функцию
![]() так, чтобы функция
так, чтобы функция
![]() удовлетворяла и второму условию из (3),
т.е. чтобы частная производная по у
от функции, стоящей в правой части
формулы (4), была тождественно равна
функции
удовлетворяла и второму условию из (3),
т.е. чтобы частная производная по у
от функции, стоящей в правой части
формулы (4), была тождественно равна
функции
![]() .
Для этого достаточно потребовать, чтобы
.
Для этого достаточно потребовать, чтобы
![]() удовлетворяла условию
удовлетворяла условию
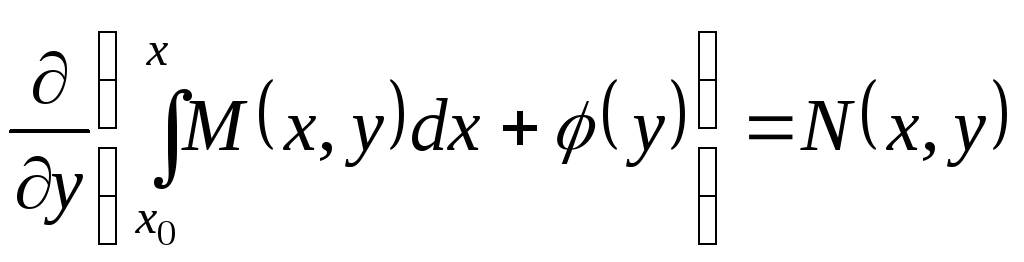 .
.
Заметим, что
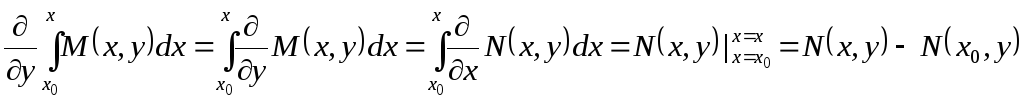 .
.
Поэтому
![]()
или
![]() ,
,
откуда
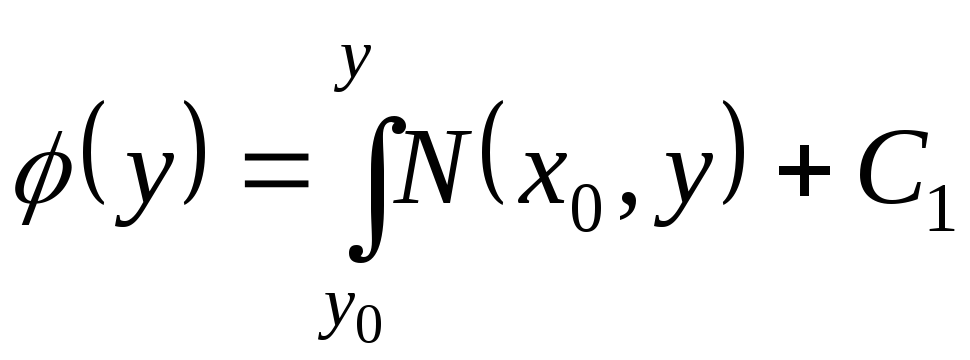 .
.
Подставляя найденное
значение
![]() в формулу (4), получим искомую функцию
в формулу (4), получим искомую функцию
![]() в виде
в виде
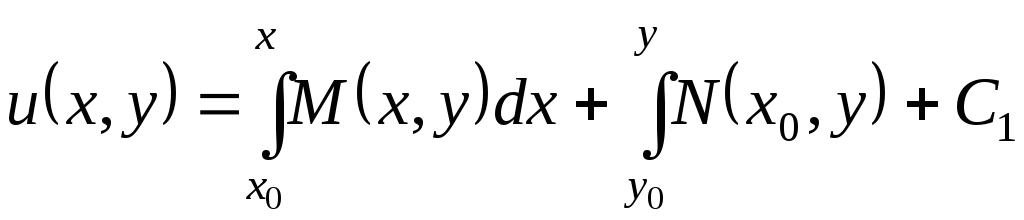 .
.
Теорема доказана.
Подставляя найденную
функцию
![]() в формулу
в формулу
![]() и полагая
и полагая
![]() ,
получим общий интеграл уравнения (1) в
виде
,
получим общий интеграл уравнения (1) в
виде
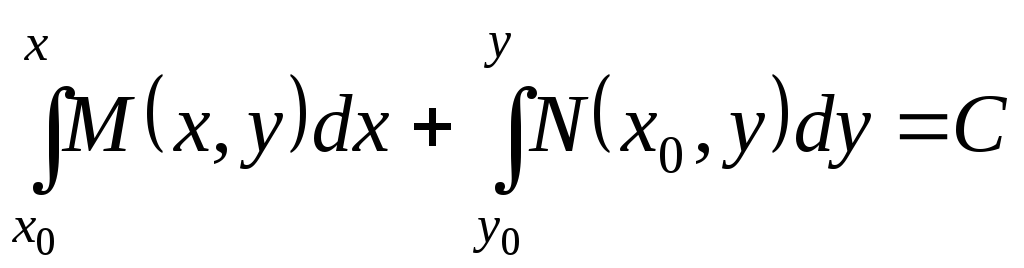 . (5)
. (5)
Пример.
Рассмотрим уравнение
![]() .
.
Решение.
Здесь
![]() ,
,
![]() ,
так что условие (2) выполнено и,
следовательно, данное уравнение есть
уравнение в полных дифференциалах.
Применяя формулу (5) при
,
так что условие (2) выполнено и,
следовательно, данное уравнение есть
уравнение в полных дифференциалах.
Применяя формулу (5) при
![]() ,
получим общий интеграл исходного
дифференциального уравнения в виде
,
получим общий интеграл исходного
дифференциального уравнения в виде
![]()
или
![]() .
.
В некоторых, правда
весьма редких, случаях, когда уравнение
(1) не является уравнением в полных
дифференциалах, все же удается подобрать
функцию
![]() ,
после умножения на которую левая часть
(1) превращается в полный дифференциал
,
после умножения на которую левая часть
(1) превращается в полный дифференциал
![]() .
.
Такая функция называется интегрирующим множителем. Из определения интегрирующего множителя имеем
![]()
или
![]() ,
,
![]() ,
,
откуда
![]() ,
,
![]() . (6)
. (6)
Таким образом, для нахождения интегрирующего множителя мы получили уравнение в частных производных.
Отметим некоторые частные случаи, когда удается сравнительно легко найти решение уравнения (6), т.е. найти интегрирующий множитель.
1.
![]() .
Тогда
.
Тогда
![]() и уравнение (6) примет вид
и уравнение (6) примет вид
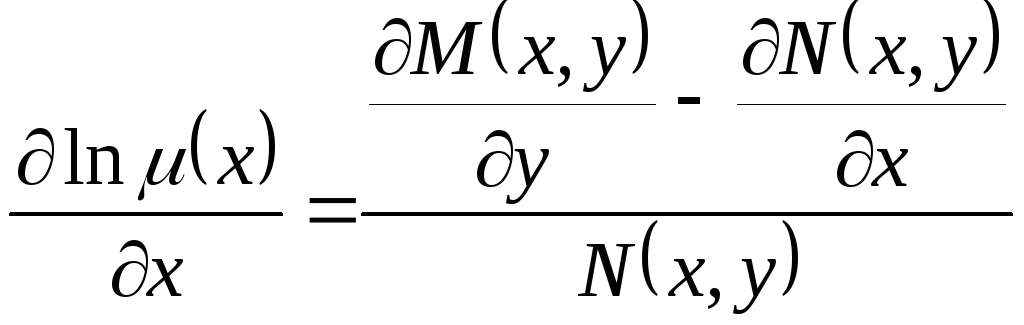 .
.
Для существования интегрирующего множителя, не зависящего от у, необходимо и достаточно, чтобы правая часть последнего равенства была функцией только от х.
Пример.
Рассмотрим уравнение
![]() .
.
Решение.
Здесь
![]() ,
,
![]() .
.
Имеем
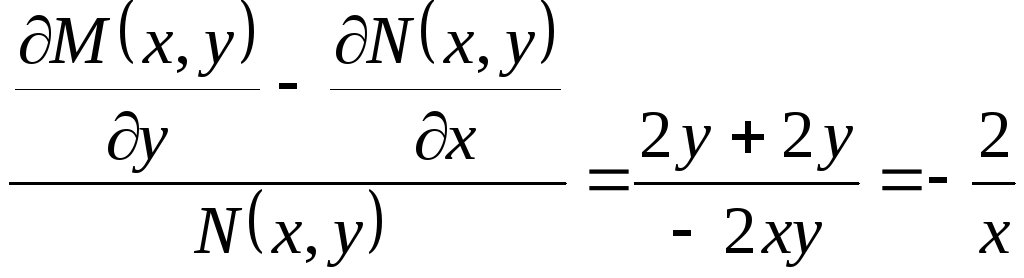 .
.
Следовательно,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Уравнение
![]()
есть уравнение в полных дифференциалах. Решите это уравнение самостоятельно.
2. Аналогично , если
![]() .
Тогда
.
Тогда
![]() и уравнение (6) примет вид
и уравнение (6) примет вид
![]() ,
,
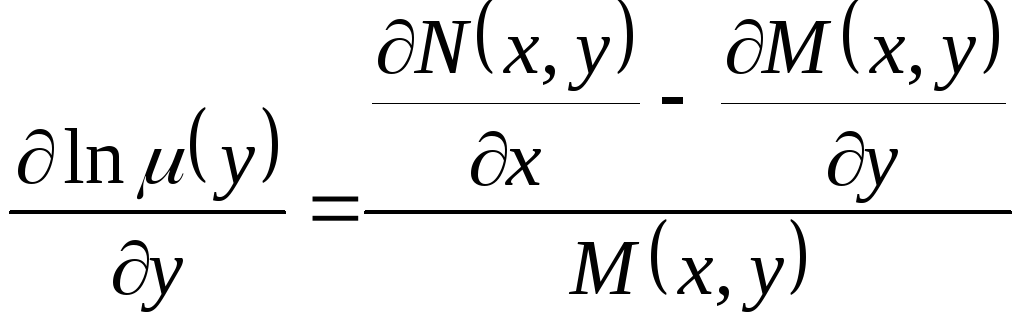 .
.
Для существования интегрирующего множителя, не зависящего от х, необходимо и достаточно, чтобы правая часть последнего равенства была функцией только от у.
Пример.
![]() .
.
Решение.
Здесь
![]() ,
,
![]() .
Имеем
.
Имеем
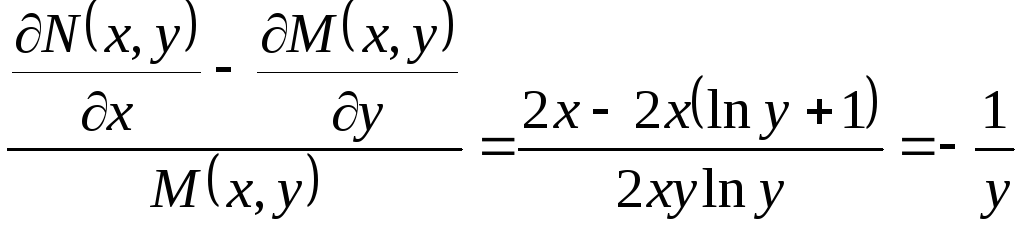 .
.
Следовательно,
![]() ,
,
![]() ,
,
![]() .
.
Уравнение
![]()
является уравнением в полных дифференциалах. Решите это уравнение самостоятельно.
8. Уравнения Лагранжа и Клеро.
Уравнение вида
![]() , (7)
, (7)
линейные относительно х и у, называется уравнением Лагранжа.
Уравнение (7) может
быть проинтегрировано путем введения
параметра
![]() .
Действительно,
.
Действительно,
![]() ,
,
![]() .
.
Но
![]() и, следовательно,
и, следовательно,
![]()
или
![]() .
.
В результате мы
получили линейное по отношению к х
и
![]() уравнение, которое легко может быть
проинтегрировано методом вариации
постоянной. Интеграл этого линейного
уравнения
уравнение, которое легко может быть
проинтегрировано методом вариации
постоянной. Интеграл этого линейного
уравнения
![]() совместно с уравнением
совместно с уравнением
![]()
определяет интегральные кривые исходного уравнения.
Пример. Проинтегрировать уравнение
![]() .
.
Решение.
Полагаем
![]() .
Тогда
.
Тогда
![]() .
.
Дифференцируя, находим
![]() ,
,
откуда
![]() или
или
![]() .
.
Получили уравнение 1-го порядка, линейное относительно х. Решая его, находим
![]() ,
,
![]() ,
,
![]() .
.
Подставляя найденное значение х в выражение для у, окончательно получим
![]() ,
,
![]() ,
,
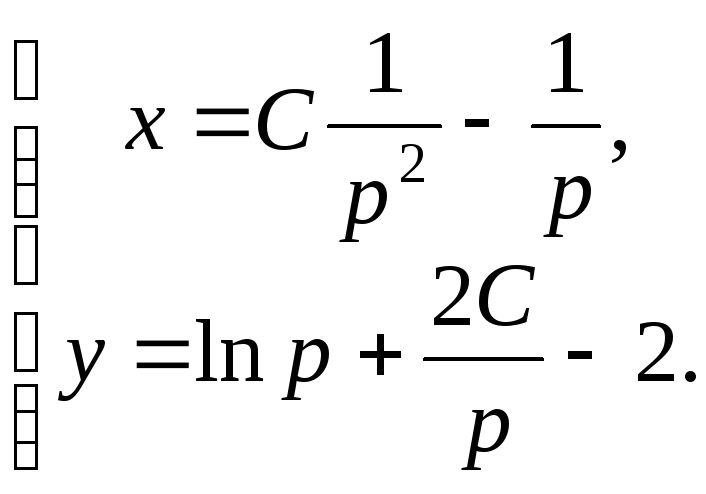
Интересный частный
случай возникает, если в уравнении
Лагранжа
![]() ,
т.е. когда уравнение имеет вид
,
т.е. когда уравнение имеет вид
![]() . (8)
. (8)
Уравнение, имеющее вид (8) называется уравнением Клеро.
Полагая
![]() ,
получим
,
получим
![]()
и, дифференцируя,
найдем:
![]() или
или
![]() ,
откуда
,
откуда
1.
![]() ,
,
![]() или 2.
или 2.
![]() .
.
Общее решение уравнения Клеро имеет вид
![]() .
.
Уравнение Клеро
может иметь еще особое решение, которое
получается исключением р
из уравнений
![]() ,
,
![]() .
.
Пример. Проинтегрировать уравнение
![]() ,
,
![]() .
.
Решение.
Полагая
![]() ,
получим
,
получим
![]() .
.
Дифференцируя
последнее уравнение и заменяя
![]() на
на
![]() ,
найдем
,
найдем
![]() ,
,
откуда
![]() .
.
Исследуем оба множителя левой части последнего уравнения. Приравнивая к нулю первый множитель, получим
![]() ,
,
откуда
![]() и общее решение исходного уравнения
есть
и общее решение исходного уравнения
есть
![]() .
.
Приравнивая к нулю второй множитель, будем иметь
![]() .
.
Исключая р
из этого уравнения и из уравнения
![]() ,
получим
,
получим
![]() - особое решение исходного уравнения.
- особое решение исходного уравнения.
